03-Logistic回归算法_logist.fit-优快云博客

本文链接：https://blog.youkuaiyun.com/WSY_nian/article/details/131554562

ps：本文所有代码都在上面的资源里，可自行下载

一、梯度下降法实现逻辑回归

1、生成分类数据

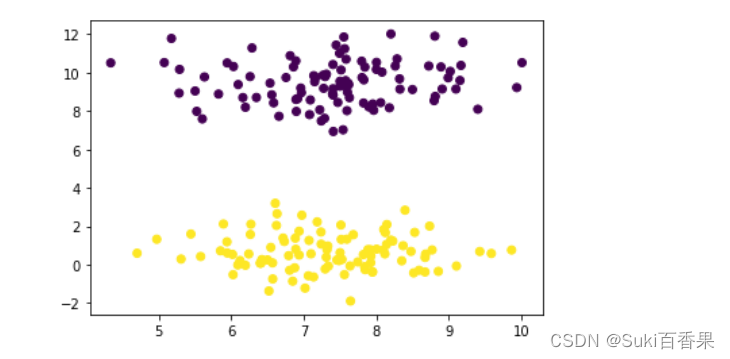
利用sklearn中的datasets库中的make_blobs生成200条二分类数据，数据可视化如图所示。

#生成200条二分类数据（2个特征）
from sklearn.datasets import make_blobs
X,y = make_blobs(n_samples= 200,n_features=2,centers =2,random_state=8)
#数据可视化
import matplotlib.pyplot as plt
plt.scatter(X[:,0],X[:,1],c=y)

2、梯度下降法实现逻辑回归

梯度下降算法

$\theta _{j} :=\theta _{j} -\frac{a}{m} \sum_{i=1}^{m} (h_{\theta }(x^{(i)})-y^{(i)})x_{j}^{(i)}$

$h_{\theta } (x)=\frac{1}{1+e^{-\theta ^{T} x} }$

#添加全一列
import pandas as pd 
import numpy as np
x_ones=np.ones((X.shape[0],1))
X=np.hstack((X,x_ones))

拆分训练集和测试集

#拆分数据
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3,random_state=8)

查看数据维度

#查看数据维度
print(X.shape,X_train.shape,X_test.shape)
print(y.shape,y_train.shape,y_test.shape)

将因变量转为列变量

#将因变量转为列变量
y_trian = y_train.reshape(-1,1)
y_test = y_test.reshape(-1,1)
print(y_trian.shape,y_test.shape)

初始化theta值

theta=np.ones([X_train.shape[1],1])
theta

定义sigmoid函数，计算出每一次迭代的theta值

#设置步长
alpha=0.001
m=140
num_iters=10000
#定义sigmoid函数
def sigmoid(z):
    s=1.0/(1+np.exp(-z))
    return s
for i in range(num_iters):
    h = sigm