算法学习|Day14-二叉树|Leetcode144二叉树的前序遍历，Leetcode145二叉树的后序遍历，Leetcode94二叉树的中序遍历

一、Leetcode144(二叉树的前序遍历)

题目描述

给你二叉树的根节点 root ，返回它节点值的 前序 遍历。

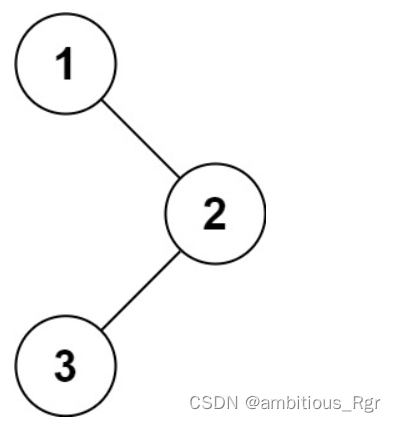
输入：root = [1,null,2,3]
输出：[1,2,3]

输入：root = []
输出：[]

输入：root = [1]
输出：[1]

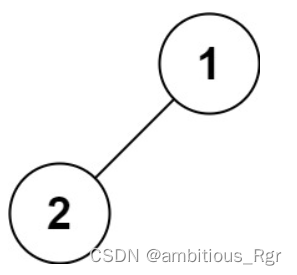
输入：root = [1,2]
输出：[1,2]

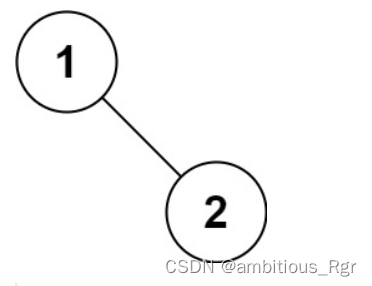
输入：root = [1,null,2]
输出：[1,2]

题目链接：力扣题目链接

解题思路

• 确定递归函数的参数和返回值
• 确定终止条件
• 确定单层递归的逻辑

方法一:递归

• 递归函数的参数就是当前节点，返回list数组
• 终止条件就是当前节点为Null
• 单层递归的逻辑是中左右

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
      def preorder(root:TreeNode):
        if not root:
          return
        res.append(root.val)
        preorder(root.left)
        preorder(root.right)

      res = list()
      preorder(root)
      return res
        

方法二:迭代

• 用栈，后进先出的顺序
• 所以压入栈内需要按照中右左的顺序
• 先处理头结点

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        # 非递归方法
        # 先判断根节点
        if not root:
            return []
        res = []
        stack = [root]

        while stack:
            node = stack.pop()
            res.append(node.val)
            # 放入根节点的左右节点 注意先右后左!!
            if node.right:
                stack.append(node.right)
            if node.left:
                stack.append(node.left)
        return res
        

总结

• 递归实现的时候传入的是root节点，加入list数组的是root.val的值
• 迭代法用栈实现的时候注意是中右左
• 递归判断条件是节点为空，迭代判断条件是栈为空

---

二、Leetcode145(二叉树的后序遍历)

题目描述

给你一棵二叉树的根节点 root ，返回其节点值的 后序遍历 。

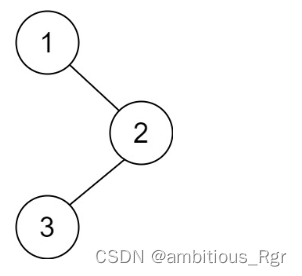
输入：root = [1,null,2,3]
输出：[3,2,1]

输入：root = []
输出：[]

输入：root = [1]
输出：[1]

题目链接：力扣题目链接

解题思路

• 确定递归函数的参数和返回值
• 确定终止条件
• 确定单层递归的逻辑

方法一:递归

• 递归函数的参数就是当前节点，返回list数组
• 终止条件就是当前节点为Null
• 单层递归的逻辑是左右中

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        def postorder(root: TreeNode):
            if not root:
                return
            postorder(root.left)
            postorder(root.right)
            res.append(root.val)

        res = list()
        postorder(root)
        return res

方法二:迭代

• 因为前序是中左右，后续是左右中
• 后序可以先从前序的中左右，变换成中右左(后续的倒序)
• 最后再倒序输出
• 先处理头结点

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        # 非递归方法
        # 先判断根节点
        if not root:
            return []
        res = []
        stack = [root]

        while stack:
            node = stack.pop()
            res.append(node.val)
            # 放入根节点左右孩子
            if node.left:
                stack.append(node.left)
            if node.right:
                stack.append(node.right)
        # 从前序的中左右，变成中右左，最后返回倒置
        return res[::-1]

总结

• 迭代法的后序可以从前序变换成中右左，再倒序输出
• 倒序输出为res[::-1]
• 递归判断条件是节点为空，迭代判断条件是栈为空

---

三、Leetcode94(二叉树的中序遍历)

题目描述

给定一个二叉树的根节点 root ，返回 它的 中序 遍历 。

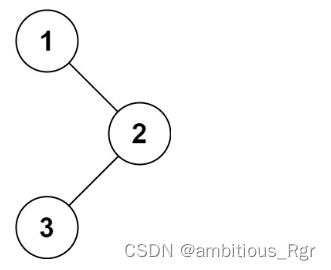
输入：root = [1,null,2,3]
输出：[1,3,2]

输入：root = []
输出：[]

输入：root = [1]
输出：[1]

题目链接：力扣题目链接

解题思路

• 确定递归函数的参数和返回值
• 确定终止条件
• 确定单层递归的逻辑

方法一:递归

• 递归函数的参数就是当前节点，返回list数组
• 终止条件就是当前节点为Null
• 单层递归的逻辑是左中右

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        def inorder(root: TreeNode):
            if not root:
                return
            inorder(root.left)
            res.append(root.val)
            inorder(root.right)

        res = list()
        inorder(root)
        return res

方法二:迭代

• 判断条件是当节点和栈不为空
• 将左分支的节点都压入栈内，一路向左
• 当节点为空的时候就出栈，加入list，再向右分支走
• 先处理头结点

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        # 非递归方法
        # 先判断根节点
        if not root:
            return []
        res = []
        stack = [] # 不能将root加入到stack中
        cur = root

        while cur or stack:
            if cur:
                stack.append(cur)
                cur = cur.left
            else:
                cur = stack.pop()
                res.append(cur.val)
                cur = cur.right

        return res

总结

• 迭代法的中序比较复杂，跟前序后续不同，当节点存在时是一直向左压入栈，当节点为空栈不为空时开始压栈，加入list，再向右走
• 递归判断条件是节点为空，迭代判断条件是节点和栈为空(因为一开始栈为空但是节点不为空，需要进入while循环)

---

心得：毕设交完旅游完，接上Day15，第一天就上强度了，深度优先搜索的前序中序后序还需要多看几遍，包括递归和迭代法，秋招赶不上就春招，先把基础打好！