周周报报

枯木逢春不在茂，年少且惜镜边人

今天来学习一下
大数乘法

大数乘法的过程相当于模拟人的手算过程

#include<stdio.h>
#include<string.h>
char a[100],b[100],c[10000],aa[100],bb[100];
int main()
{
 int i,j=0,m,n,flag=0;
 scanf("%s %s",aa,bb);
 m=strlen(aa);
 n=strlen(bb);
 for(i=m-1;i>=0;i--)//逆序存入，是为了从个位算起
 a[j++]=aa[i]-'0';
 j=0;
 for(i=n-1;i>=0;i--)
 b[j++]=bb[i]-'0';
 for(i=0;i<m;i++)
    for(j=0;j<n;j++)//c[i+j]是巧妙的进行了位置转变，也隐含算术时的进位
    {
     c[i+j]+=a[i]*b[j];
    }
 for(i=0;i<10000;i++)//结果大于等于10的当然要进位上去
 {
  if(c[i]>=10)
  {
   c[i+1]+=c[i]/10;
   c[i]=c[i]%10;
  }
 }
 for(i=10000;i>=0;i--)//从第一个不是0的数字开始输出最高位
 {
  if(flag==1)
  {
   printf("%d",c[i]);
  }
  else if(c[i])
  {
   printf("%d",c[i]);
   flag=1;
     }
 }
 if(flag==0)//如果是0乘以任何数 那当然是0喽
 {
  printf("0");
 }
 return 0;
}

大数乘法相对来书挺好理解的，大家都会懂，看完代码，可以用手跑一遍，也就理解的差不多了

01背包

#include<stdio.h>
int dp[100][100];
int v[100],w[100];
int max(int a,int b)
{
 return a>b?a:b;
}
int main()
{
 int i,j,m,n;
 scanf("%d %d",&n,&m);
 for(i=1;i<=n;i++)
  scanf("%d %d",&v[i],&w[i]);
 for(i=1;i<=n;i++)
  for(j=1;j<=m;j++)
  {
   if(w[i]>j)
   dp[i][j]=dp[i-1][j];
   else
   dp[i][j]=max(dp[i-1][j-w[i]]+v[i],dp[i-1][j]);
  }
 for(i=0;i<=n;i++)
 {
  for(j=0;j<=m;j++)
  printf("%d\t",dp[i][j]);
  printf("\n");
 }
 
 
  return 0;
}

这个是二维数组
下面将一下优化

#include<stdio.h>
int dp[100];
int v[100],w[100];
int max(int a,int b)
{
 return a>b?a:b;
}
int main()
{
 int i,j,m,n;
 scanf("%d %d",&n,&m);
 for(i=1;i<=n;i++)
  scanf("%d %d",&v[i],&w[i]);
 for(i=1;i<=n;i++)
  for(j=m;j>=w[i];j--)
  {
   dp[j]=max(dp[j-w[i]]+v[i],dp[j]);
   }
   printf("%d",dp[m]);
  return 0;
}

一维数组中在第二个for循环的时候，从背包体积开始，这种一定要从最大体积开始，不然dp[]会覆盖之前的或者dp不搭配东西

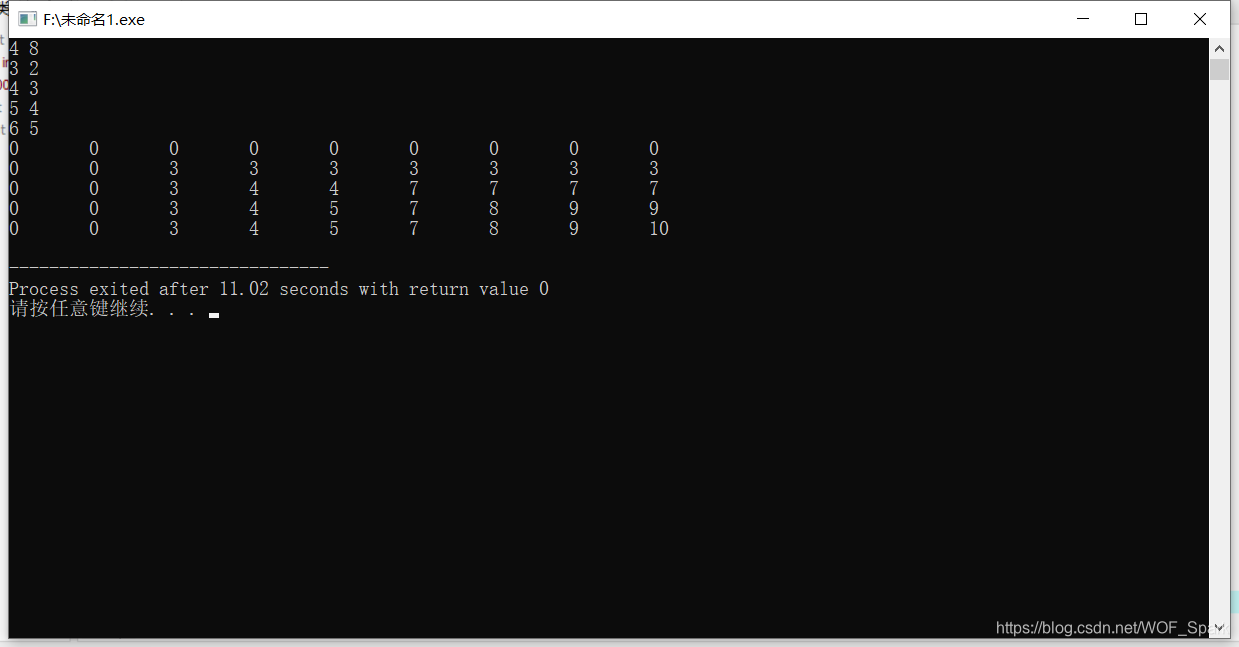
然后利用了一组测试数据大家可以看一下
不知道为什么图片查入就像坏了所以这个的测试图片放在最后
3.
下面是完全背包
：完全背包：有N种物品和一个容量为V的背包。第i种物品最多有n[i]件可用，每件费用是c[i]，价值是w[i]。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量，且价值总和最大。
先不多说看代码吧

#include<stdio.h>
int dp[300];
int w[300],v[300];
int max(int a,int b)
{
 return a>b?a:b;
}
int main()
{
 int i,j,m,n;
 scanf("%d %d",&n,&m);
 for(i=1;i<=n;i++)
 scanf("%d %d",&v[i],&w[i]);
 for(i=1;i<=n;i++)
  for(j=w[i];j<=m;j++)
  {
   dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
  }
  printf("%d",dp[m]);
} 

这就是完全背包的优化，用一位数组进行计算，与01背包不同的是，在第二个for循环的时候是顺序的，而01是逆序的，逆序保证不重复利用物品，顺序保证重复利用，秒啊！
下面看一下二维数组解法

#include<stdio.h>
int dp[300][300];
int w[300],v[300];
int max(int a,int b)
{
 return a>b?a:b;
}
int main()
{
 int i,j,m,n;
 scanf("%d %d",&n,&m);
 for(i=1;i<=n;i++)
 scanf("%d %d",&v[i],&w[i]);
 for(i=1;i<=n;i++)
   for(j=1;j<=m;j++)
   {
    dp[i][j]=dp[i-1][j];
    if(w[i]<=j)
    dp[i][j]=max(dp[i][j],dp[i][j-w[i]]+v[i]);
   }
 printf("%d",dp[n][m]);
} 

这二维数组解的话就一个公式

if(w[i]<=j)
    dp[i][j]=max(dp[i][j],dp[i][j-w[i]]+v[i]);

dp[i][j-w[i]]+v[i]

这个表示至少装一个，注意前面的i没有变，就知道这个里面可能有也可能么有，但我们至少保证了有一个，而前面的表示没有装这个东西。

多重背包

#include<stdio.h>
int dp[300];
int w[300],s[300],v[300];
int m;
int max(int a,int b)
{
 return a>b?a:b;
}
void lingyi(int weight,int value)
{
 int i;
 for(i=m;i>=weight;i--)
 dp[i]=max(dp[i],dp[i-weight]+value);
}
void wanquan(int weight,int value)
{
 int i;
 for(i=weight;i<=m;i++)
 {
  dp[i]=max(dp[i],dp[i-weight]+value);
 }
}
void duochong(int weight,int value,int number)
{
 int k=1;
 if(m<=number*weight)
 {
  wanquan(weight,value);
  return ;
 }
 else
 {
  while(k<=number)
  {
   lingyi(k*weight,k*value);
   number=number-k;
   k=2*k;
  }
  lingyi(number*weight,number*value);
 }
} 
int main()
{
 int i,j,n;
 scanf("%d %d",&n,&m);
 for(i=0;i<n;i++)
 {
  scanf("%d %d %d",&s[i],&v[i],&w[i]);
 }
 for(i=0;i<n;i++)
 {
  duochong(w[i],v[i],s[i]);
 }
 printf("%d",dp[m]);
} 

多重背包其实是01背包和完全背包的一个统一结合运用
对于一个数量k，例如13，我们可以把它分解成 1 2 4 6
这些是怎么分的呢？首先从1开始，依次乘2，最后当剩下的不足时，全部以01背包解决，实际上每一个数量都可以看成这么多件物品处理，如果这种物品的总重量大于背包体积，那么就只能用相当于这个物品全部装，也就是完全背包。
4.
所以我们今天来看一下
bfs
dfs
首先看一下dfs吧
写一个全排列问题吧

#include<stdio.h>
int n;
int  a[10],book[10];
void dfs(int step)
{
 int i;
 if(step==n+1)
 {
  for(i=1;i<=n;i++)
  printf("%d",a[i]);
  printf("\n"); 
  return ;
 } 
 for(i=1;i<=n;i++)
 {
  if(book[i]==0)
  {
   a[step]=i;
   book[i]=1;
   dfs(step+1);
   book[i]=0;
  }
 }
 return ;
}
int main()
{
 scanf("%d",&n);
 dfs(1);
 return 0;
} 

手中有N张牌，放入n个箱子里面，问有多少种放法
首先从第一个箱子开始，判断手中的牌是不是用过了，没有用过，则这步就用这张并标记，标记完后边开始下一步，然后再把标记了的清空，是下一次是顺利取牌。
5…
好了再看看bfs
都是最简单，难点的还有点小小的问题

#include<stdio.h>
int a[51][51],book[51][51];
struct f
{
   int x,y,s; 
};
int main()
{
 struct f que[51];
 int head,tail;
 int next[4][2]={{0,1},{1,0},{0,-1},{-1,0}};
 int startx,starty,tx,ty,p,q,flag,i,j,k,m,n;
 scanf("%d %d",&m,&n);
 for(i=1;i<=m;i++)
   for(j=1;j<=n;j++)
   scanf("%d",&a[i][j]);
 scanf("%d %d %d %d",&startx,&starty,&p,&q);
 tail=1;
 head=1;
 que[tail].x=startx;
 que[tail].y=starty;
 que[tail].s=0;
 tail++;
 book[startx][starty]=1;
 flag=0;
 while(head<tail)
 {
  for(i=1;i<=3;i++)
  {
   tx=que[head].x+next[i][0];
   ty=que[head].y+next[i][1];
   if(tx<1||tx>m||ty<1||ty>n)
   {
    continue;
   }
   if(a[tx][ty]==0&&book[tx][ty]==0)
   {
    book[tx][ty]=1;
    que[tail].x=tx;
    que[tail].y=ty;
    que[tail].s=que[head].s+1;
    tail++;
   }
   if(tx==p&&ty==q)
   {
    flag=1;
    break;
      }
  }
  if(flag==1)
  break;
  head++;
 }
 printf("%d",que[tail-1].s);
 return 0;
}

这就是宽搜，宽搜是用队列的方式进行搜索，从head出发看从head出发的路径有几条，然后一起进行探索，相当于宽搜就是一边过，不回去，所以没有book=0这一说，宽搜是一步可以走出多步的形式，另外宽搜的题在我的博客，acm第二周里面有提到过，粗略的讲了讲
that`s all;