SVM

间隔与支持向量机
目的：在样本空间中找到一个划分超平面，将不同类别的样本分开。
在样本空间中，超平面的方程可以通过线性方程来表示
1
w=(w1,w2…wd)为法向量，决定超平面的方向，b为位移项，决定了超平面与远点之间的距离。
样本空间中任意一点到该平面的距离为：
2
设超平面（w,b）能将训练样本正确分类，即对于（wi,yi）属于D,若取值为+/-1

3
使得3式成立的训练样本点被称为支持向量，两个异类支持向量到超平面的距离为：

4
4式被称为间隔，
要找到最大间隔，就是要找到能满足1式中约束参数的w和b，使得r最大

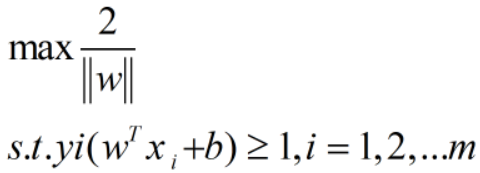5
为最大间隔化，需将||w||-1，等价于最小化||w||2,于是得

6
这就是支持向量机SVM的基本型。
对偶问题：
求解6式得到最大间隔划分超平面所对应的模型
7
利用拉格朗日乘子法，对6式加入拉格朗日乘子，其拉格朗日函数为：
8
对w和b求偏导，带入8式，可以消去w和b，
9
得到6.6式的对偶问题

10
当约束条件为不等式时，需要满足KKT条件

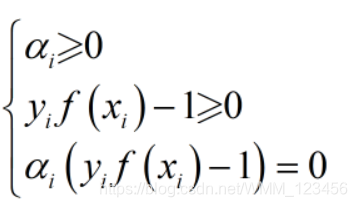
支持向量机的一个重要性质为：训练完成后，大部分的训练样本都不需要保留，最终的模型与支持向量有关。

SMO算法的基本思想：先固定ai之外的所有参数，然后求解ai上的极值，存在约束条件aiyi=0(i=1,2,3…m),如果固定ai之外的其他变量，则ai可由其他变量导出，所以SMO每次选择两个变量ai和aj，并固定其他参数，正在参数初始化后，SMO不断执行如下两个步骤，直到收敛

1，选取一对需要更新的变量ai和aj
2，固定ai和aj以外的参数，求解最终的对偶问题10。

核函数：将样本从原始空间映射都爱高维空间的得变换。

核函数广泛应用的原因：

1，核函数引入避免了位数灾难，减少了计算量，输入空间的维数n对核函数矩阵无影响，所以核函数能够有效初六高维输入。
2，无需知道非线性变换函数的形式和参数。
3，核函数方法可以和不同的算法相结合，形成不同的基于核函数技术的大方法，且这两部分可以单独记性，并为不同的应用选择不同的核函数的算法。