 C题
C题
🧩题意总结
有 n 个小朋友围成一圈,每人说:
-
1表示「左边的朋友会说真话」; -
0表示「左边的朋友会说假话」。
问:所有 2ⁿ 种可能的“真话/假话分配”中,有多少种分配使得所有小朋友的陈述都正确?
结果对 998244353 取模。
✅核心思路

🔁 环上的一致性条件
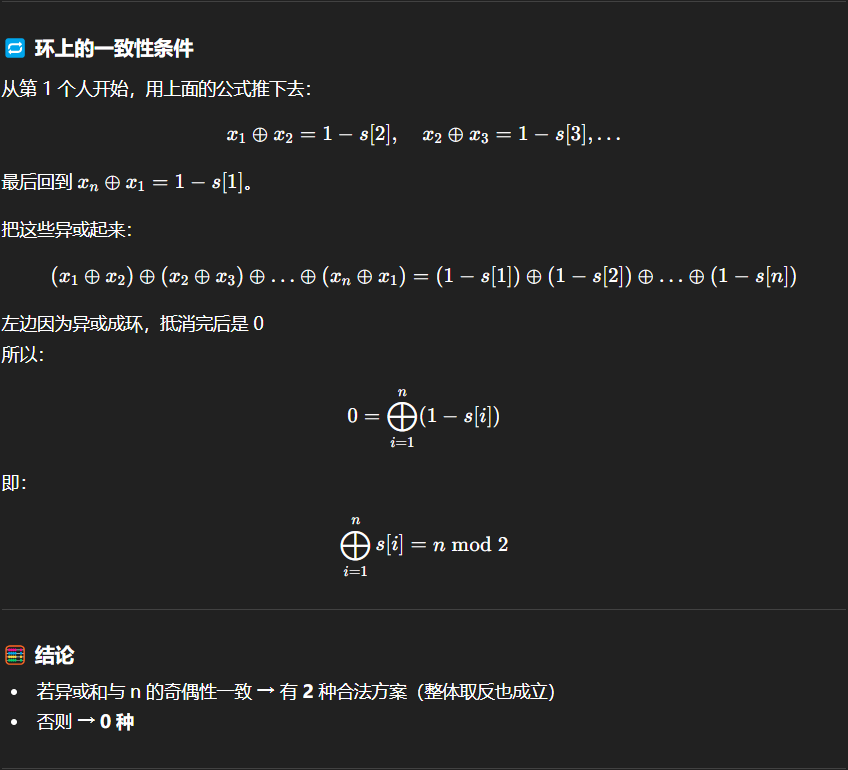
🧮 结论
-
若异或和与 n 的奇偶性一致 → 有 2 种合法方案(整体取反也成立)
-
否则 → 0 种
💻 Java 实现
//Java快读快写模板
import java.io.*;
import java.math.BigDecimal;
import java.math.BigInteger;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
Read sc = new Read();
//从n循环到0 for (int i = n;i>=0; i--)
//输入a+b+c+d+e+f//int a = sc.nextInt(),b = sc.nextInt(),c = sc.nextInt(),d = sc.nextInt(),e = sc.nextInt(),f = sc.nextInt();
//输入数组 //int n = sc.nextInt();int[] a=new int[n];for (int i = 0; i < n; i++) {a[i]=sc.nextInt();}
//IDEA快速生成变量声明的快捷键是 Ctrl + Alt + V。
//next()方法适用于读取不带空格的单个单词,而nextLine()方法适用于读取包含空格的完整行输入。
// 范围!!范围!!范围!!范围!!范围!!范围!!范围!!范围!!范围!!范围!!范围!!范围!!
// Long!涉及大数!的 加乘!都要Long!!!!!!!!!!!!!!!!!超过int的运算至少要一个Long!!!!!!!!!!!!
// ******************************************************************************************************************************************************
int t = sc.nextInt();
long inf = 998244353L;
// 123456798
while (t-- > 0) {
int n = sc.nextInt();
String s = sc.next();
/*int num1 = 0, num0 = 0;
if (n % 2 == 1) {
boolean bb = false;
for (int i = n - 1; i > !!!!!!!!!; i--) {
if (s.charAt(i) == '0') {
bb = true;
int num = 1;
for (int k = i - 1; k > 0; k--) {
if (s.charAt(k) == '0') {
num++;
}
}
if (num % 2 == 1) {
num0++;
}else {
num0+=2;
}
} else if (s.charAt(i - 1) == '1') {
num1++;
}
}
if (s.charAt(0) == '0')
if (s.charAt(1) == '0')
if (bb) {
System.out.println(0);
break;
}
}
boolean[] b = new boolean[n];
for (int i = 0; i < n; i++) {
b[i] = s.charAt(i) == '1';
}
if (num1 == num0)
System.out.println(2);
else
System.out.println(0);*/
int num = 0;
for (int i = 0; i < n; i++) {
if (s.charAt(i) == '0') num ^= 0;
}
if (num == (n % 2))
System.out.println(2);
else
System.out.println(0);
}
//******************************************************************************************************************************************************
sc.flush();
sc.bw.close();
}
}
//s.substring(0,i)+s.substring(j+1) //String删除i到j
//map.put( Key , map.getOrDefault(chars[i],0) + 1 );key的值++
//map.getOrDefault(key,0) 如果key存在,返回key对应的值,如果不存在,返回0
//使用contains方法 List,可以用contains方法来判断是否包含特定的字符串 boolean b=stringList.contains(s);
//等比Sn= a1(1-qn)/(1-q) =(a1-an*q)/(1-q)
//等差Sn= n*a1+n(n-1)/2*d =n(a1+an)/2
// 倒序List Collections.reverse(new ArrayList<>());
//优先队列 Queue<String> q = new PriorityQueue<>(new Comparator<String>()规则);默认是小根堆。
//字符串降序排列比较规则 String::compareTo 或 (s1, s2) -> s2.compareTo(s1)
//Integer降序排列比较规则 (a, b)->b-a
//int[]降序排列Arrays.sort(a,(s,b)->b-s);
//str1.compareTo(str2); 返回前减后// 比较字符串的大小compareTo()方法是区分大小写的。如果需要忽略大小写进行比较,可以使用compareToIgnoreCase()方法
//将k四舍五入y位System.out.printf("%."+y+"f\n",k)
//exp()函数,exp(x)=e^x
//立方根 Math.cbrt(n) 平方sqrt()
//分割字符串s.substring()
//GCD方法*最小公约数 BigInteger.gcd(bbb)));
//判断三个整数能否构成一个三角形 if (canFormTriangle(a, b, c));public static boolean canFormTriangle(int a, int b, int c) {return (a > 0 && b > 0 && c > 0) && (a + b > c && a + c > b && b + c > a); }
//取模的数字,别少写(int)1e9+7,inf别写错类型(long)8e18
//初始化数据的时候,最小值不要傻乎乎的默认为0,因为可能有负数
//记住看数字范围,需要开long吗,需要用BigInteger吗,需要手动处理字符串吗,复杂度数量级控制在1e7或者以下了吗
//开数组的数据范围最高不能超过1e7,数据范围再大就要用哈希表离散化了
//基本数据类型不能自定义sort排序,二维数组就可以了,顺序排序的时候是小减大,注意返回值应该是int
//BFS的时候记得在循环里要往队列里push,拓扑排序要确认无环
//“>>”运算的时候,int和long类型得到的数字可能是不同的
class Read {
BufferedReader bf;
StringTokenizer st;
BufferedWriter bw;
public Read() {
bf = new BufferedReader(new InputStreamReader(System.in));
st = new StringTokenizer("");
bw = new BufferedWriter(new OutputStreamWriter(System.out));
//什么时候才能持续稳定ak力扣、AcWing呢?
//什么时候才能ak cf的div2,(div1)呢?才能打div2不计rating呢?
//什么时候才能ak abc arc 不计rating呢?
//什么时候才能ak 牛客练习赛不计rating呢?
//什么时候才能ak 洛谷的div2呢?才能打div2不计rating呢?
}
//输入部分:
public String nextLine() throws IOException {
return bf.readLine();
}
public String next() throws IOException {
while (!st.hasMoreTokens()) {
st = new StringTokenizer(bf.readLine());
}
return st.nextToken();
}
public char nextChar() throws IOException {
//确定下一个token只有一个字符的时候再用
return next().charAt(0);
}
public int nextInt() throws IOException {
return Integer.parseInt(next());
}
public long nextLong() throws IOException {
return Long.parseLong(next());
}
public double nextDouble() throws IOException {
return Double.parseDouble(next());
}
public float nextFloat() throws IOException {
return Float.parseFloat(next());
}
public byte nextByte() throws IOException {
return Byte.parseByte(next());
}
public short nextShort() throws IOException {
return Short.parseShort(next());
}
public BigInteger nextBigInteger() throws IOException {
return new BigInteger(next());
}
public BigDecimal nextDecimal() throws IOException {
return new BigDecimal(next());
}
//以下为输出部分::
public void println(int a) throws IOException {
print(a);
println();
}
public void print(int a) throws IOException {
bw.write(String.valueOf(a));
}
public void println(String a) throws IOException {
print(a);
println();
}
public void print(String a) throws IOException {
bw.write(a);
}
public void println(long a) throws IOException {
print(a);
println();
}
public void print(long a) throws IOException {
bw.write(String.valueOf(a));
}
public void println(double a) throws IOException {
print(a);
println();
}
public void print(double a) throws IOException {
bw.write(String.valueOf(a));
}
public void print(BigInteger a) throws IOException {
bw.write(a.toString());
}
public void print(char a) throws IOException {
bw.write(String.valueOf(a));
}
public void println(char a) throws IOException {
print(a);
println();
}
public void println() throws IOException {
bw.newLine();
}
//其他调试命令:
public void flush() throws IOException {
//交互题分组调试,或者提前退出的情况下可以先运行此语句再推出
bw.flush();
}
public boolean hasNext() throws IOException {
//本地普通IDE难以使用这个方法调试,需要按照数据组flush,刷新语句:
//sc.flush()
//调试完可删去
return bf.ready();
}
}
//Trie插入新节点后,下降的命令放在if外面
⏱️ 复杂度分析
| 项目 | 复杂度 |
|---|---|
| 单组处理 | O(n) |
| 总体复杂度 | O(Σn) ≤ 2×10⁶ |
| 空间复杂度 | O(1) |
🧠 总结
环形逻辑 → 异或约束 → 环一致性条件。
判断是否满足 Σ s[i] % 2 == n % 2 即可,
答案要么 0,要么 2,非常优雅的结论。
D题
🧩 题解:区间选数最大化 MEX
一、题目理解
我们有 nnn 个区间 [li,ri][l_i, r_i][li,ri],要求从每个区间中选择一个整数,使得最终选出的所有数的集合的 MEX(最小未出现的非负整数)最大。
🌰 举例说明
例如:
区间: [0, 2] [2, 4] [6, 10]
-
我们可以选:
-
从
[0, 2]选 0 -
从
[2, 4]选 1 -
[6, 10]中无法选出能接着覆盖 2~5 的数
→ 因此,最大 MEX = 5
-
二、思路分析
要最大化 MEX,本质上是要让我们选的数字从 0 开始尽量连续覆盖。
但题目要求每个区间必须选一个数,这就变成了一个“区间与整数的匹配问题”。
⚙️ 关键观察
-
每当我们要“尝试选择数字
x”时,所有能覆盖x的区间都可以拿来用; -
但我们只能从其中选一个区间;
-
为了不影响后续更大的数字,我们应当优先选右端点最小的区间(贪心策略)。
这样能保证后续的可选空间最大,从而得到最大 MEX。
三、算法设计
整体流程如下:
🪜 步骤 1:按左端点排序
把所有区间按 l 从小到大排序。
🪜 步骤 2:使用最小堆维护“可选区间”
维护一个最小堆(PriorityQueue),用于存放当前所有能覆盖当前 mex 的区间的右端点。
🪜 步骤 3:从 0 开始尝试选择数字
设 mex = 0,表示我们现在要尝试选择数字 0。
循环执行以下操作:
-
把所有满足
l <= mex的区间加入堆; -
移除堆中所有
r < mex的区间(这些已经不能覆盖当前数字); -
如果堆为空,说明没有区间能覆盖
mex,此时的mex就是最大 MEX; -
否则,从堆中取出右端点最小的区间,用它“选择数字
mex”,并mex++; -
重复以上步骤,直到堆空。
四、算法示例
以输入:
3 0 2 2 4 6 10
为例:
| mex | 可加入的区间 | 堆(按 r 排序) | 操作 | 新 mex |
|---|---|---|---|---|
| 0 | [0,2] | {2} | 取出 [0,2] | 1 |
| 1 | [2,4] | {4} | 取出 [2,4] | 2 |
| 2 | [2,4] 已取完 | {} | 无区间可选 | 停止 |
| ✅ 最大 MEX | 5 |
(最后一次取出的右端点是 4,覆盖到了 4 → MEX = 5)
五、代码实现(Java)
import java.io.*;
import java.util.*;
public class Main {
static class Interval {
int l, r;
Interval(int l, int r) {
this.l = l;
this.r = r;
}
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sb = new StringBuilder();
int T = Integer.parseInt(br.readLine().trim());
while (T-- > 0) {
int n = Integer.parseInt(br.readLine().trim());
Interval[] segs = new Interval[n];
for (int i = 0; i < n; i++) {
String[] parts = br.readLine().trim().split(" ");
int l = Integer.parseInt(parts[0]);
int r = Integer.parseInt(parts[1]);
segs[i] = new Interval(l, r);
}
// Step 1: 按左端点排序
Arrays.sort(segs, (a, b) -> a.l - b.l);
// Step 2: 使用最小堆维护右端点
PriorityQueue<Integer> pq = new PriorityQueue<>();
int idx = 0, mex = 0;
// Step 3: 按数值逐步推进
while (true) {
// 把所有能覆盖 mex 的区间放入堆
while (idx < n && segs[idx].l <= mex) {
pq.offer(segs[idx].r);
idx++;
}
// 清除右端点 < mex 的区间
while (!pq.isEmpty() && pq.peek() < mex) pq.poll();
if (pq.isEmpty()) {
// 当前 mex 无法被覆盖 -> 最大 MEX 找到
sb.append(mex).append('\n');
break;
}
// 贪心选择右端点最小的区间,覆盖当前 mex
pq.poll();
mex++;
}
}
System.out.print(sb.toString());
}
}
六、复杂度分析
| 操作 | 时间复杂度 |
|---|---|
| 排序区间 | O(nlogn)O(n \log n)O(nlogn) |
| 每个区间入堆 + 出堆各一次 | O(nlogn)O(n \log n)O(nlogn) |
| 总体 | O(nlogn)O(n \log n)O(nlogn) |
| 空间复杂度 | O(n)O(n)O(n) |
七、算法正确性证明(简述)
-
每次我们选取右端点最小的区间,是为了保证后续区间仍有最大的可用范围;
-
贪心策略不会错过更优解,因为任何覆盖当前
mex的区间都等价,但右端点更小的会让未来更灵活; -
当堆为空时,说明没有区间能再覆盖当前
mex,因此当前的mex一定是最大 MEX。
✅ 八、总结
| 优点 | 说明 |
|---|---|
| 高效 | 只需排序 + 一次扫描即可完成 |
| 贪心正确 | 始终选右端点最小的区间最优 |
| 稳定 | 能处理大量数据(n ≤ 2×10⁵) |
| 清晰 | 每一步都有物理意义(代表选了哪个数) |
加油!看不懂问农





















 347
347

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








