poj 1179 Polygon

Polygon

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 4407		Accepted: 1839

Description

Polygon is a game for one player that starts on a polygon with N vertices, like the one in Figure 1, where N=4. Each vertex is labelled with an integer and each edge is labelled with either the symbol + (addition) or the symbol * (product). The edges are numbered from 1 to N.

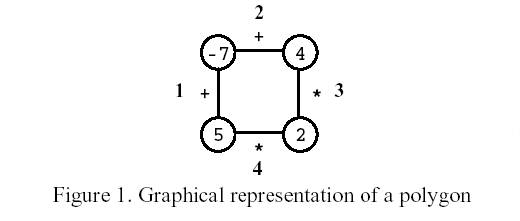
On the first move, one of the edges is removed. Subsequent moves involve the following steps:
�pick an edge E and the two vertices V1 and V2 that are linked by E; and
�replace them by a new vertex, labelled with the result of performing the operation indicated in E on the labels of V1 and V2.
The game ends when there are no more edges, and its score is the label of the single vertex remaining.

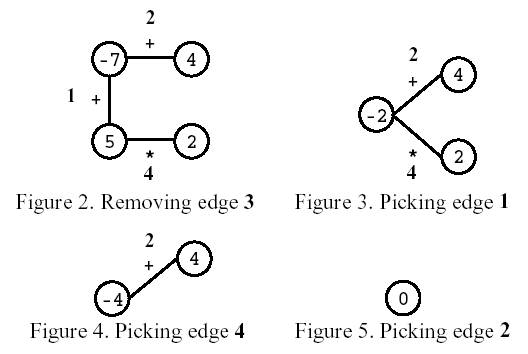
Consider the polygon of Figure 1. The player started by removing edge 3. After that, the player picked edge 1, then edge 4, and, finally, edge 2. The score is 0.

Write a program that, given a polygon, computes the highest possible score and lists all the edges that, if removed on the first move, can lead to a game with that score.

Input

Your program is to read from standard input. The input describes a polygon with N vertices. It contains two lines. On the first line is the number N. The second line contains the labels of edges 1, ..., N, interleaved with the vertices' labels (first that of the vertex between edges 1 and 2, then that of the vertex between edges 2 and 3, and so on, until that of the vertex between edges N and 1), all separated by one space. An edge label is either the letter t (representing +) or the letter x (representing *).

3 <= N <= 50
For any sequence of moves, vertex labels are in the range [-32768,32767].

Output

Your program is to write to standard output. On the first line your program must write the highest score one can get for the input polygon. On the second line it must write the list of all edges that, if removed on the first move, can lead to a game with that score. Edges must be written in increasing order, separated by one space.

Sample Input

4
t -7 t 4 x 2 x 5

Sample Output

33
1 2

多边形游戏是一个单人玩的游戏，开始时有一个由n个顶点构成的多边形。每个顶点被赋予一个整数值，每条边被赋予一个运算符“+”或“*”。所有边依次用整数从1到n编号。
游戏第1步，将一条边删除。
随后n-1步按以下方式操作：
(1)选择一条边E以及由E连接着的2个顶点V1和V2；
(2)用一个新的顶点取代边E以及由E连接着的2个顶点V1和V2。将由顶点V1和V2的整数值通过边E上的运算得到的结果赋予新顶点。
最后，所有边都被删除，游戏结束。游戏的得分就是所剩顶点上的整数值。

问题:对于给定的多边形，计算最高得分。分析：
• 在所给多边形中，从顶点i(1≤i≤n)开始，长度为j(链中有j个顶点)的顺时针链p(i，j) 可表示为v[i]，op[i+1]，…，v[i+j-1]。
• 如果这条链的最后一次合并运算在op[i+s]处发生(1≤s≤j-1)，则可在op[i+s]处将链分割为2个子链p(i，s)和p(i+s，j-s)。
• 设m1是对子链p(i，s)的任意一种合并方式得到的值，而a和b分别是在所有可能的合并中得到的最小值和最大值。m2是p(i+s，j-s)的任意一种合并方式得到的值，而c和d分别是在所有可能的合并中得到的最小值和最大值。依此定义有a≤m1≤b，c≤m2≤d
(1)当op[i+s]=’+'时，显然有a+c≤m≤b+d
(2)当op[i+s]=’*'时，有min{ac，ad，bc，bd}≤m≤max{ac，ad，bc，bd}
换句话说，主链的最大值和最小值可由子链的最大值和最小值得到。

AC代码：

#include <iostream>
#include <cstring>
#include <string>
#include <cstdio>
#include <algorithm>
#include <queue>
#include <cmath>
#include <vector>
#include <cstdlib>

using namespace std;
const int maxn=55;
const int maxnum=999999999;
const int minnum=-999999999;
int maxv[maxn][maxn];  //maxv[i][j]i到j合并后的最大值
int minv[maxn][maxn];  //minv[i][j]i到j合并后的最小值
int val[maxn];     //结点上的权值
char op[maxn];     //操作符
int ansmax;        //储存临时的最大结果
bool dedge[maxn]; //最大结果所删除的边
int n;
void init()       //初始化
{
    for(int i=0;i<n;i++)
    for(int j=0;j<n;j++)
    {
        if(i==j)
        maxv[i][j]=minv[i][j]=val[i];
        else
        {
            maxv[i][j]=minnum;
            minv[i][j]=maxnum;
        }
    }
}
int main()
{
    int deledge,steplen,j,tempmax,tempmin;
    while(cin>>n)
    {
        for(int i=0;i<n;i++)
            cin>>op[i]>>val[i];
        ansmax=minnum;
        for(deledge=0;deledge<n;deledge++)  //对每条边进行删除遍历
        {
            init();
            for(steplen=2;steplen<=n;steplen++)  //对应所删边的步长
            {
                for(int i=deledge;i<=n+deledge-steplen;i++) //遍历对应步长的起始位置
                {
                    j=i+steplen-1;  //对应的起始位置的终点位置
                    for(int k=i;k<j;k++) //遍历断点k
                    {
                        int kleftmax=maxv[i%n][k%n];
                        int kleftmin=minv[i%n][k%n];
                        int krightmax=maxv[(k+1)%n][j%n];
                        int krightmin=minv[(k+1)%n][j%n];
                        if(op[(k+1)%n]=='t')
                        {
                            tempmax=kleftmax+krightmax;
                            tempmin=kleftmin+krightmin;
                        }
                        else
                        {
                            tempmax=max(max(kleftmax*krightmax,kleftmin*krightmin),max(kleftmax*krightmin,kleftmin*krightmax));
                            tempmin=min(min(kleftmax*krightmax,kleftmin*krightmin),min(kleftmax*krightmin,kleftmin*krightmax));
                        }
                        maxv[i%n][j%n]=max(maxv[i%n][j%n],tempmax);
                        minv[i%n][j%n]=min(minv[i%n][j%n],tempmin);
                    }
                }
            }
            if(maxv[deledge][(deledge+n-1)%n]>ansmax)
            {
                memset(dedge,0,sizeof(dedge));
                ansmax=maxv[deledge][(deledge+n-1)%n];
                dedge[deledge]=1;
            }
            else if(maxv[deledge][(deledge+n-1)%n]==ansmax)
            dedge[deledge]=1;
        }
        cout<<ansmax<<endl;
        for(int i=0;i<n;i++)
        if(dedge[i])
        cout<<i+1<<" ";
        cout<<endl;
    }
    return 0;
}