[DA45] 信用卡诈骗分析

一. 相关介绍

    (一) 类不平衡问题

        在机器学习分类任务中, 类别不平衡是指不同类别的训练样例数差别很大.

        解决类不平衡问题的方法有过抽样、欠抽样、阈值移动和组合方法等, 一般来讲后两种方法的效果高于前两种方法. 

        更多详细内容请查看百度百科: 类不平衡问题

    (二) 精确率 - 召回率曲线

        sklearn 中的 precision_recall_curve 函数可以通过预测值和真实值来计算精确率 - 召回率曲线.

        该函数通过传入样本的真实类别模型预测样本的置信分数, 返回精确率数组、召回率数组和对应的阈值数组，通过 matplot.pyplot 工具绘制曲线, 反应了不同概率阈值情况下的精确率和召回率.

    (三) ROC 曲线与 AUC 

        接受者操作特性曲线, 又称为感受性曲线, 它是一种非常有效的模型评价方法, 可为选定临界值给出定量提示. 将灵敏度设在纵轴, 1-特异性设置在横轴, 就可以得出 ROC 曲线图.

        与精确率 - 召回率曲线类似, sklearn 中的 roc_curve 函数, 返回的是假正例率 fpr 数组、真正例率 tpr 数组和对应的阈值数组. 

        AUC 被定义为 ROC 曲线下与坐标轴围成的面积, 它的大小与每种模型优劣密切相关, 反映分类器正确分类的统计概率. 由于ROC 曲线一般都处于 y = x 这条直线的上方, 所以 AUC 的取值范围在0.5和1之间.

  从AUC 判断分类器（预测模型）优劣的标准：  (以下数据摘自百度百科)

• AUC = 1，是完美分类器。

• AUC = [0.85, 0.95], 效果很好

• AUC = [0.7, 0.85], 效果一般

• AUC = [0.5, 0.7],效果较低，但用于预测股票已经很不错了

• AUC = 0.5，跟随机猜测一样（例：丢铜板），模型没有预测价值。

• AUC < 0.5，比随机猜测还差；但只要总是反预测而行，就优于随机猜测。

 

二. 数据分析 

    (一) 数据加载与探索

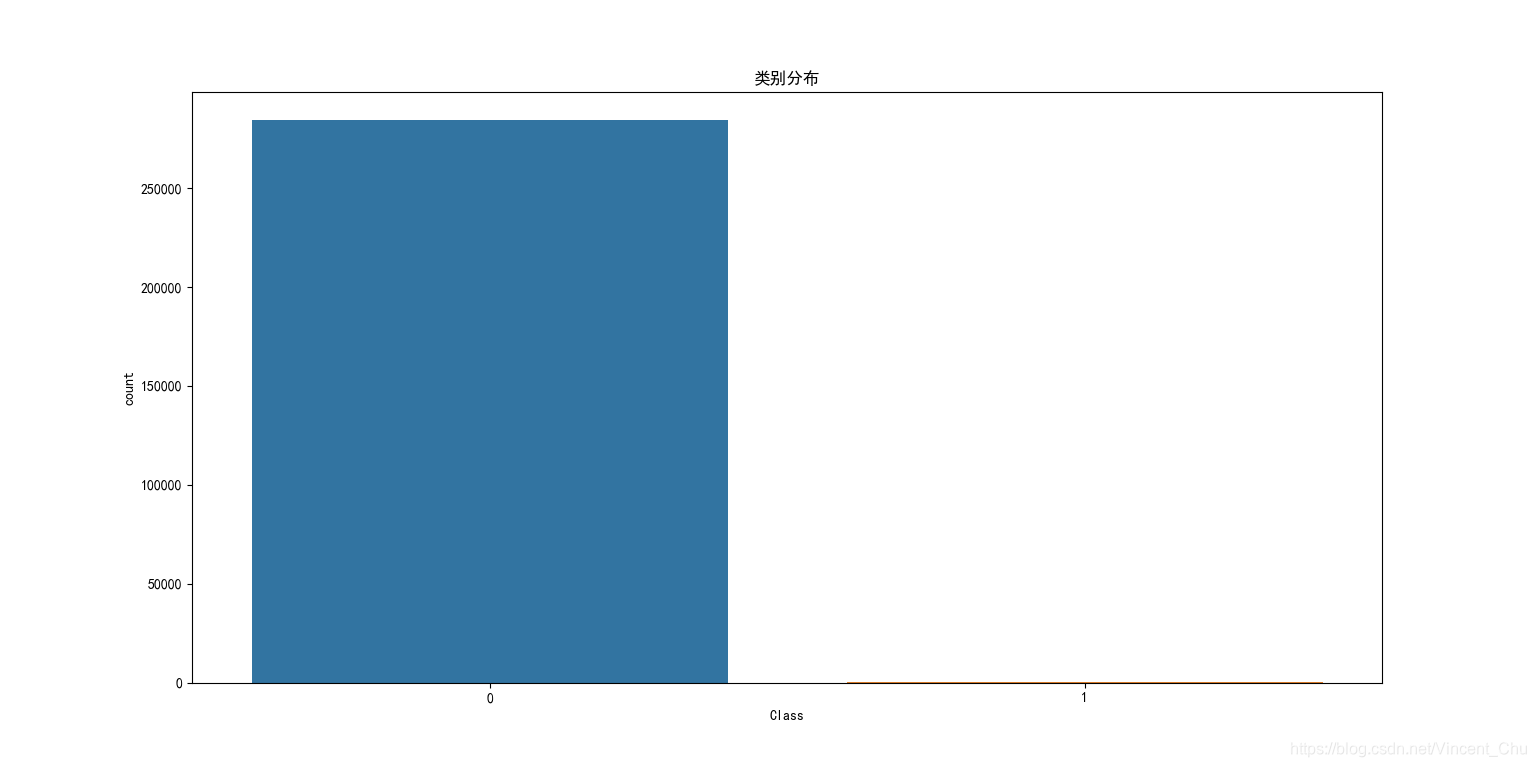
        数据为2013年9月份两天时间内的信用卡交易数据, 284807笔交易中只有492笔是欺诈行为, 由于数据分析的关注点为欺诈交易, 感兴趣的主类占比较少, 属于典型的类不平衡问题.

        输入数据一共包括了28个特征 V1 到 V28 对应的取值, 以及交易时间 Time 和交易金额 Amount. 为了保护数据隐私, 原始数据中 V1 到 V28 为 PCA 变换得到的结果. 另外字段 Class 代表该笔交易的分类, Class=0代表正常, Class=1代表欺诈. 数据中无缺失值.

正常交易数与欺诈交易数

 

从图中看出的类不平衡

 

    (二) 数据预处理

       V1 - V28 的特征值都经过 PCA 的变换, Time 和 Amount 两个字段还需要进行规范化. Time 字段和交易本身是否为欺诈交易无关, 因此不作为特征选择, 所以只需要对 Amount 做数据规范化. 同时数据没有专门的测试集, 需使用 train_test_split 对数据集进行划分, 由于是欺诈交易数较少, 传入参数 stratify=labels 确保欺诈交易与正常交易的比例一致.

        相关代码:

# 标准化
ss = StandardScaler()
data['Amount'] = ss.fit_transform(data['Amount'].values.reshape(-1, 1))

# 准备训练集和测试集
labels = data['Class'].values
features = data.drop(['Time', 'Amount', 'Class'], axis=1).values
train_x, test_x, train_y, test_y = train_test_split(features, labels, test_size=0.1, stratify=labels)

    (三) 建模与预测

        使用逻辑回归模型进行分类, 由于本次分析的关注点不在于类不平衡问题样本数据的优化, 故直接使用第(二)步处理好的数据进行训练与预测.

        因为数据集存在类不平衡问题, 故不能使用一般的评价方式对模型进行评定, 在此使用了 f1得分、模型评价报告、混淆矩阵对模型进行了大致评估, 代码与结果如下:

# 定义混淆矩阵可视化函数
def cm_plot(data_matrix):
    sns.heatmap(data_matrix, annot=True, fmt='d', cmap='Greens')
    ax = plt.gca()
    ax.xaxis.set_ticks_position('top')  # x 轴刻度显示在顶端
    ax.xaxis.set_label_position('top')  # x 轴标签显示在顶端
    ax.spines['right'].set_color('none')
    ax.spines['bottom'].set_color('none')
    plt.ylabel('True label')
    plt.xlabel('Predicted label')
    plt.show()


# 逻辑回归分类
clf = LogisticRegression()
clf.fit(train_x, train_y)
predict_y = clf.predict(test_x)

# f1得分
f1 = f1_score(test_y, predict_y)
print('f1得分:', f1)

# 模型评价
report = classification_report(test_y, predict_y)
print(report)

# 混淆矩阵
matrix = confusion_matrix(test_y, predict_y)
cm_plot(matrix)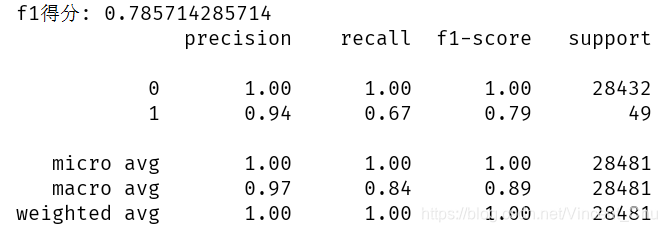

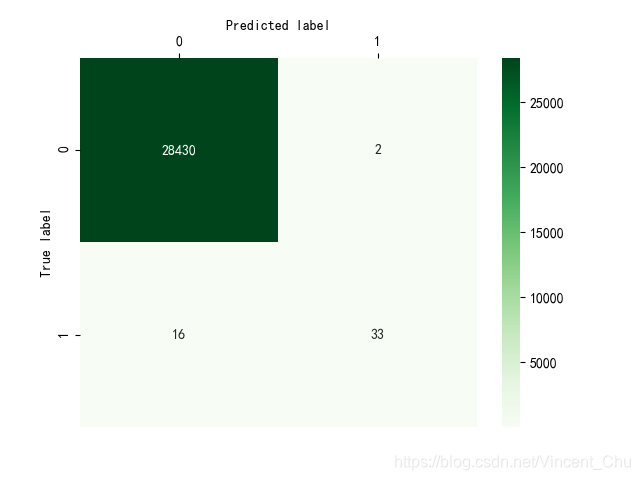
f1 得分 与 模型评价报告

混淆矩阵可视化

 

        从混淆矩阵中可以看出, 测试集中有正常交易 (28430 + 2) 例, 欺诈交易 (16 + 33) 例, 有 2 例正常的交易被模型误判为欺诈交易, 有 16 例欺诈交易被模型误判为了正常交易.

        精确率 P = TP / (TP + FP) = 33 / (33 + 2) = 0.94

        召回率 R = TP / (TP + FN) = 33 / (33 + 16)  = 0.67

        f1 得分为 0.79

    (四) 曲线绘制

        绘制精确率 - 召回率曲线与 ROC 曲线, 再通过两种方法计算 ROC 曲线的 AUC 值.

    相关代码:

# 定义曲线函数
def curve_plot(x_data, y_data, x_label, y_label, title_name):
    plt.plot(x_data, y_data, linewidth=2)
    plt.fill_between(x_data, y_data, step='post', alpha=0.2, color='b')
    plt.title(title_name)
    plt.xlabel(x_label)
    plt.ylabel(y_label)
    plt.xlim(0, 1.05)
    plt.ylim(0, 1.05)
    plt.show()


# 样本的置信分数
score_y = clf.decision_function(test_x)

# 精确率-召回率 曲线
precision, recall, thresholds1 = precision_recall_curve(test_y, score_y)
curve_plot(precision, recall, '精确率', '召回率', '精确率-召回率 曲线')

# ROC 曲线
fpr, tpr, thresholds2 = roc_curve(test_y, score_y)
curve_plot(fpr, tpr, '假正例率', '真正例率', 'ROC 曲线')

# 计算 AUC
print('AUC_1:', roc_auc_score(test_y, score_y))
print('AUC_2:', auc(fpr, tpr))

        

 

 

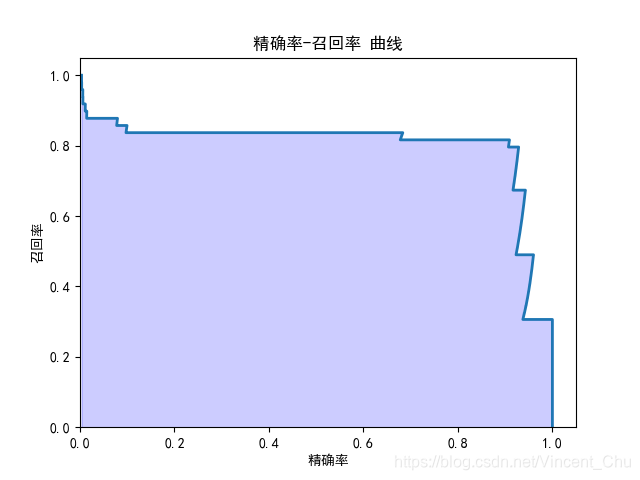
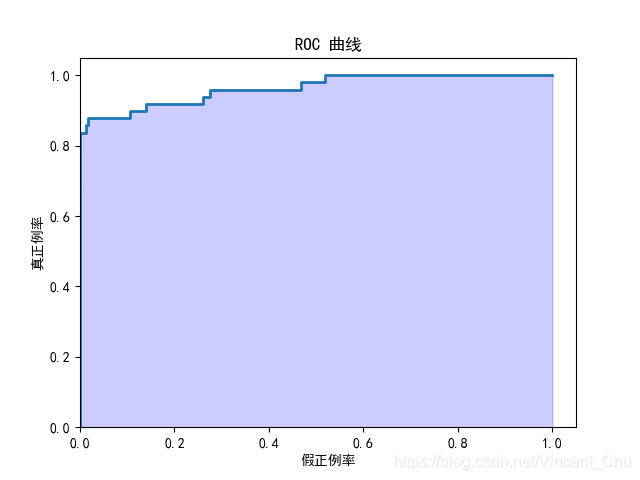
        由计算得 AUC 值为 0.96 , 对比百度百科的 AUC 评判优劣标准, 该逻辑回归分类器属于比较好的分类器.

        但是从混淆矩阵上看, 分类器的精确率虽然较高, 但是召回率并不理想, 而且从精确率 - 召回率曲线上看, 阈值移动可提高召回率, 但精确率的牺牲也比较大, 为了解决这种类不平衡问题, 还是需要考虑使用更好的方法, 在此不做进一步分析.