本文介绍了统计学中衡量数据离散程度的几个关键指标，包括极差、四分位差、方差与标准差，以及偏态系数和峰态系数。极差和四分位差用于描述数据的分布集中程度，方差和标准差则揭示了数据波动的大小。偏态系数和峰态系数进一步揭示了数据分布的对称性和尖峰程度。此外，还概述了统计指标的类型，如绝对数、相对数、平均数和质量指标，这些是理解和分析数据时的重要工具。
1、极差与四分位差（R）
1）极差：称为全距，极大值减去极小值所得；主要用于衡量能否代表一组数据
2）四分位差：上四分位数-下四分位数所得；反映了中间50%数据的离散程度，数值越小说明中间的数据越集中。
3）极差与四分位差都用来判断数据的离散程度。
2、方差与标准差（西格玛、V）
1）总体方差与标准差（数据未分组时使用）
2）样本方差与标准差（数据分组过后使用）
3）方差和标准差是应用最广泛的离散程度测度值，能表明平均数是否可以代表整组数据。
4）离散系数（分析波动）
越小差异性也越小，是标准差与其均值之比：
3、偏态系数与峰态系数（SK、β）
1）偏态系数（SK）是以标准差为计量单位的算数平均数与众数之差：
-
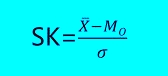
SK通常取值为-3 ~ +3之间，其绝对值大,表明偏斜程度大;反之表明偏斜程度越小。
-
当SK=0时，分布为对称分布; SK<0时，分布呈左偏分布，或称负偏态; SK>0时，
最低0.47元/天 解锁文章
扫一扫
2529
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
