树的深搜序的一些简单用途

首先，对于一棵树有很多序，比如宽搜序，深搜的先序遍历，后序遍历等。这里我们只介绍树的深搜序和欧拉序。

---

• 欧拉序

一棵树的欧拉序，就是在深搜遍历这棵树的时候，每次访问到这个节点就将其加入栈，例如下面这个图：

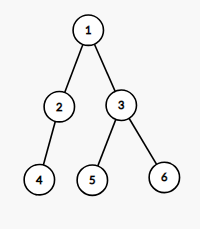
它的欧拉序就是：$[1,2,4,4,2,1,3,5,5,3,6,6,3,1]$

用途就是可以用$rmq$的$st-stable$来快速求$lca$，详解见这里【RMQ-LCA】

• dfs序

博主这里主要总结dfs序。

这个就是利用一个时间戳，在深搜过程中，记录访问到这个节点时的时间和退出访问到这个节点的时间。

例如上面那张图，访问顺序就是：

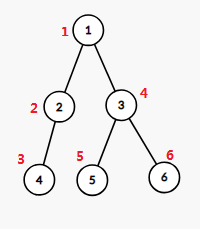
对于每个节点，第一次访问到它的时间戳和退出访问的时间戳就是：

$$\begin{gathered} 1=(1,6) \\ 2=(2,3) \\ 3=(3,3) \\ 4=(4,6) \\ 5=(5,5) \\ 6=(6,6) \end{gathered}$$

然后我们按照时间戳大小将点排序就可以得到这颗树的dfs序了：$[1,2,4,3,5,6]$

得到这个序的代码非常简单：

struct edge{
	int to,last;
	edge(){}
	edge(int a,int b):to(a),last(b){}
}g[M<<1];
int head[M],cnt;//前向星(链表)存图
int dfn[M],out[M],tim;//进入时的时间戳，出来时的时间戳，时间戳
int stk[M];//存储dfs序

void find_dfs(int a,int fa){
	dfn[a]=++tim;stk[tim]=a;
	//开始访问，记录时间戳，并加入dfs序
	for(int i=head[a];i;i=g[i].last){
		if(g[i].to==fa) continue;
		find_dfs(g[i].to,a);
	}
	out[a]=tim;//结束访问记录时间戳
}

那么这个序有什么用呢？

下面来看具体例题：

【Loj144-DFS 序 1】

题意见loj题面。

其实我们可以直接树链剖分+线段树就可以搞定题目中的操作，但是每次操作复杂度是$O(lo{g}^{2}n)$的，所以在$10^6$的数据范围内我们很难不卡常跑过。

所以我们考虑，使用dfs序。

首先我们看上面那个图的dfs序：
$$[1,2,4,3,5,6]$$

对于一号点的子树，范围刚好就是dfs序上的$1\sim 6$的点，而对于三号点的子树，范围又刚好是$4\sim 6$的点，也就刚好对应了访问到它的时间戳到结束访问的时间戳的范围，在dfs序上都是连续的一段，所以我们可以考虑对于这个序列，我们建一个线段树。

那么操作$1$，给一个节点加上一个值，就是线段树的单点修改，而操作$2$，求一个节点的子树和，那么就是在线段树上询问这个点的访问到它的时间戳到结束访问它的时间戳这个区间的和。

由于只有单点修改，区间查询，我们可以使用常数更小的树状数组来实现：

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define lowbit(a) ((a)&(-(a)))
#define ll long long
using namespace std;
const int M=1e6+10;
int n,m,rot;
struct ss{
	int to,last;
	ss(){}
	ss(int a,int b):to(a),last(b){}
}g[M<<1];
int head[M],cnt;
void add(int a,int b){
	g[++cnt]=ss(b,head[a]);head[a]=cnt;
	g[++cnt]=ss(a,head[b]);head[b]=cnt;
}

ll val[M];
int dfn[M],rf[M],tim,out[M];//rf就为dfs序
void dfs(int a,int b){
	rf[dfn[a]=++tim]=a;
	for(int i=head[a];i;i=g[i].last){
		if(g[i].to==b) continue;
		dfs(g[i].to,a);
	}
	out[a]=tim;
}
ll bit[M];
void build(){
	for(int i=1;i<=n;i++)bit[i]=val[i]-val[i-lowbit(i)];
}
void Add(int a,ll v){
	for(;a<=n;a+=lowbit(a))bit[a]+=v;
}
ll query(int a){
	ll res=1;
	for(;a;a-=lowbit(a))res+=bit[a];
	return res;
}
ll Query(int p){
	return query(out[p])-query(dfn[p]-1);
}
ll v[M];int a,b,opt;
int main(){
	scanf("%d%d%d",&n,&m,&rot);
	for(int i=1;i<=n;i++)scanf("%lld",&v[i]);
	for(int i=1;i<n;i++){
		scanf("%d%d",&a,&b);
		add(a,b);
	}
	dfs(rot,0);
	for(int i=1;i<=n;i++){val[i]=val[i-1]+v[rf[i]];}
	build();
	while(m--){
		scanf("%d%d",&opt,&a);
		if(opt==1){
			scanf("%d",&b);
			Add(dfn[a],b);
		}else{
			printf("%lld\n",Query(a));
		}
	}
	return 0;
}

---

【loj125-DFS 序 2】

这个也就是和上面那个一样了，只不过变成了区间修改区间查询，可以用差分和两个树状数组实现，但是线段树写起了要无脑简单些，所以博主用线段树实现的：

#include<cstdio>
#include<cstring>
#include<algorithm>
#define ll long long
using namespace std;
const int M=1e6+10;

int n,m,rot;
struct ss{
	int to,last;
	ss(){}
	ss(int a,int b):to(a),last(b){}
}g[M<<1];
int head[M],cnt;
void add(int a,int b){
	g[++cnt]=ss(b,head[a]);head[a]=cnt;
	g[++cnt]=ss(a,head[b]);head[b]=cnt;
}
ll val[M];
int dfn[M],rf[M],out[M],tim;
void dfs(int a,int b){
	rf[dfn[a]=++tim]=a;
	for(int i=head[a];i;i=g[i].last){
		if(g[i].to==b) continue;
		dfs(g[i].to,a);
	}
	out[a]=tim;
}

ll sum[M<<2],lazy[M<<2];
void pushup(int o){
	sum[o]=sum[o<<1]+sum[o<<1|1];
}
void pushdown(int o,int l,int r,int mid){
	if(!lazy[o]) return;
	sum[o<<1]+=1ll*(mid-l+1)*lazy[o];
	sum[o<<1|1]+=1ll*(r-mid)*lazy[o];
	lazy[o<<1]+=lazy[o];
	lazy[o<<1|1]+=lazy[o];
	lazy[o]=0;
}
void build(int o,int l,int r){
	if(l==r){
		sum[o]=val[rf[l]];
		return;
	}
	int mid=l+r>>1;
	build(o<<1,l,mid);
	build(o<<1|1,mid+1,r);
	pushup(o);
}
void update(int o,int l,int r,int L,int R,ll v){
	if(L<=l&&r<=R){
		lazy[o]+=v;
		sum[o]+=1ll*(r-l+1)*v;
		return;
	}
	int mid=l+r>>1;
	pushdown(o,l,r,mid);
	if(L<=mid)update(o<<1,l,mid,L,R,v);
	if(R>mid)update(o<<1|1,mid+1,r,L,R,v);
	pushup(o);
}
ll query(int o,int l,int r,int L,int R){
	if(L<=l&&r<=R){
		return sum[o];
	}
	int mid=l+r>>1;
	pushdown(o,l,r,mid);
	if(R<=mid) return query(o<<1,l,mid,L,R);
	else if(L>mid) return query(o<<1|1,mid+1,r,L,R);
	else return query(o<<1,l,mid,L,R)+query(o<<1|1,mid+1,r,L,R);
}
int a,b,opt;
int main(){
	scanf("%d%d%d",&n,&m,&rot);
	for(int i=1;i<=n;i++)scanf("%lld",&val[i]);
	for(int i=1;i<n;i++){
		scanf("%d%d",&a,&b);
		add(a,b);
	}
	dfs(rot,0);
	build(1,1,n);
	while(m--){
		scanf("%d%d",&opt,&a);
		if(opt==1){
			scanf("%d",&b);
			update(1,1,n,dfn[a],out[a],b);
		}else{
			printf("%lld\n",query(1,1,n,dfn[a],out[a]));
		}
	}
	return 0;
}

---

【loj146-DFS 序 3】

【loj147-DFS 序 4】

这两个题目，主要要用到树上差分了，博主后面再详细讲解先咕咕咕一会儿