数据结构：堆

最新推荐文章于 2025-11-06 17:06:47 发布

原创最新推荐文章于 2025-11-06 17:06:47 发布 · 708 阅读

2 ·

CC 4.0 BY-SA版权

C++ 专栏收录该内容

34 篇文章

订阅专栏

本文深入解析堆数据结构，包括小顶堆和大顶堆的概念，堆的存储方式，以及如何通过调整二叉树实现堆的构建。同时，文章详细介绍了堆的插入、删除操作，并探讨了TopK问题的高效解决方案。

文章目录

堆是什么？
二叉树调整成小堆
堆的增删
TopK问题

堆排序

堆是什么？

堆是将一组数据按照完全二叉树的存储顺序，将数据存储在一个一维数组中的结构。
堆有两种结构，一种称为大顶堆，一种称为小顶堆，如下图。
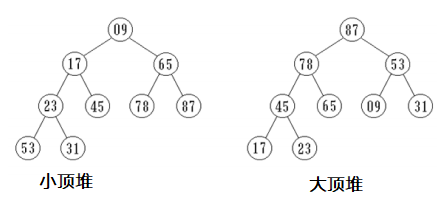
在这里插入图片描述
小顶堆：任意结点的值均小于等于它的左右孩子，并且最小的值位于堆顶，从根节点到每个结点的路径上数组元素组成的序列都是递增的。

大顶堆：任意结点的值均大于等于它的左右孩子，并且最大的值位于堆顶，从根节点到每个结点的路径上数组元素组成的序列都是递减的

堆存储在下标为0开始的数组中，因此在堆中给定下标为 $i$ 的结点时：

如果 $i = 0$ ，结点 $i$ 是根节点，没有双亲节点；否则结点 $i$ 的双亲结点为结点 $(i - 1) / 2$
如果 $2 * i + 1 < = n - 1$ ，则结点i的左孩子为结点 $2 * i + 1$ ，否则结点 $i$ 无左孩子
如果 $2 * i + 2 < = n - 1$ ，则结点i的右孩子为结点 $2 * i + 2$ ，否则结点 $i$ 无右孩子

二叉树调整成小堆

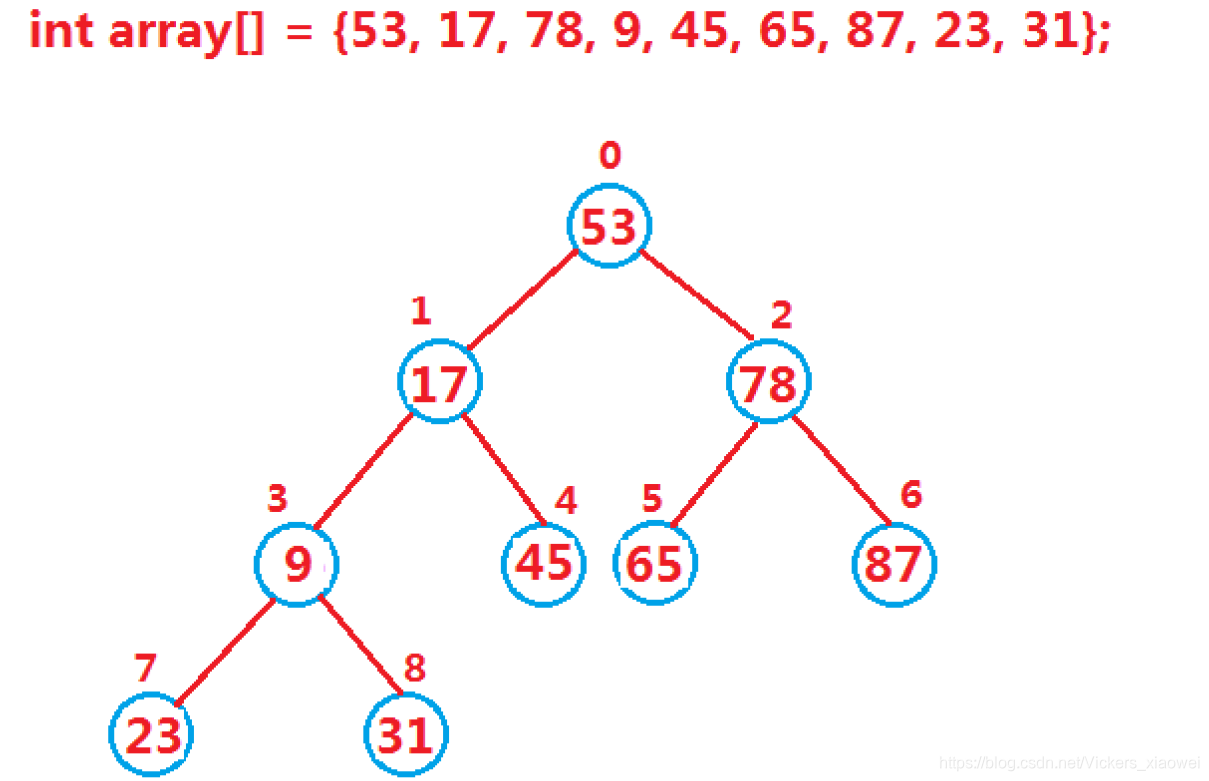
在这里插入图片描述
将二叉树调整为最小堆的原理：

从最后一个非叶子结点开始调整，一直到根节点为止，将每个结点及其子树调整到满足小堆的性质即可

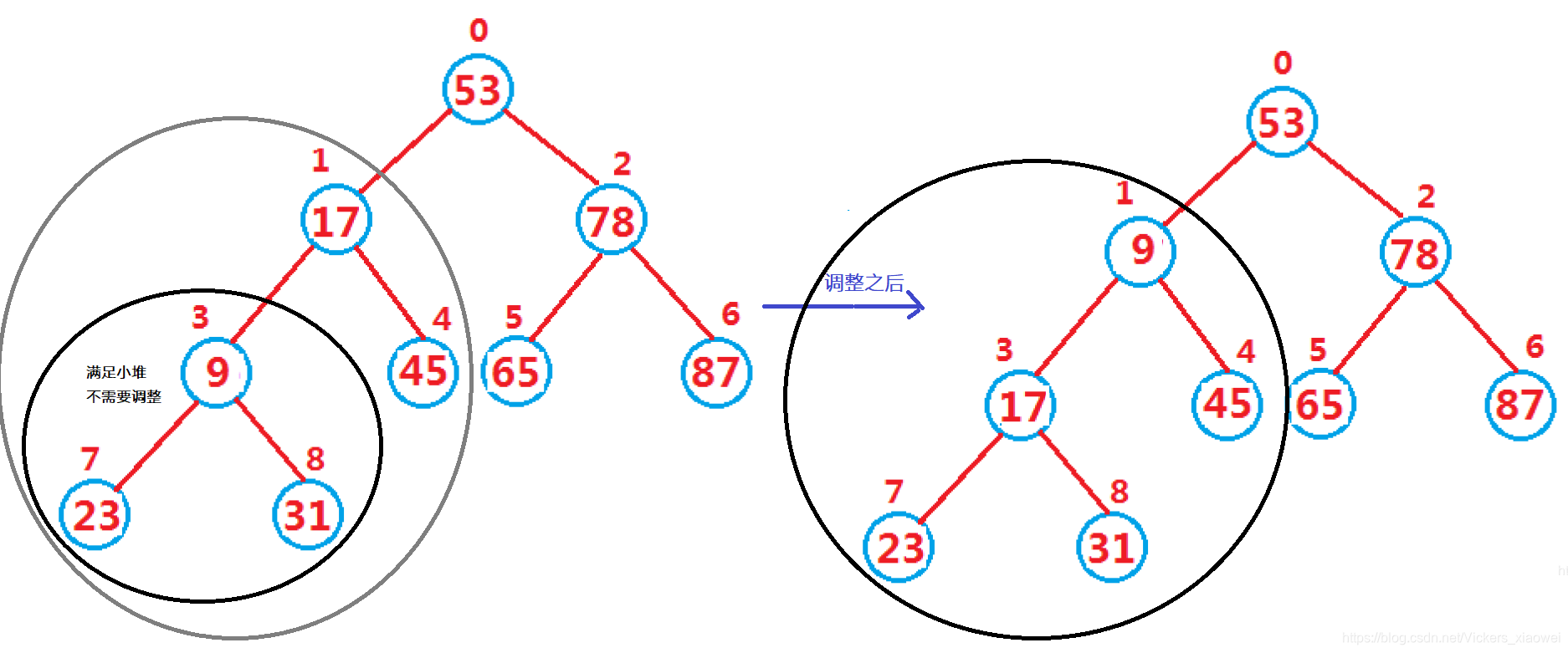
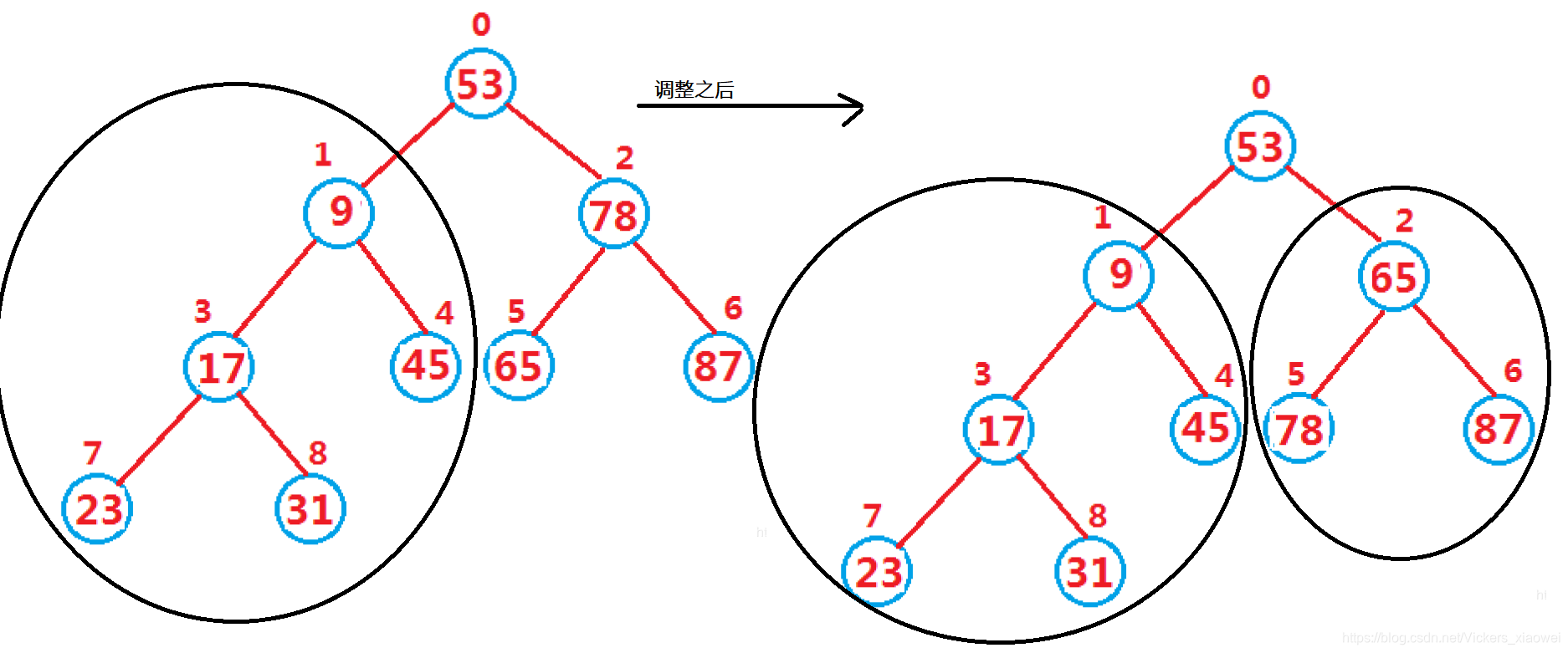
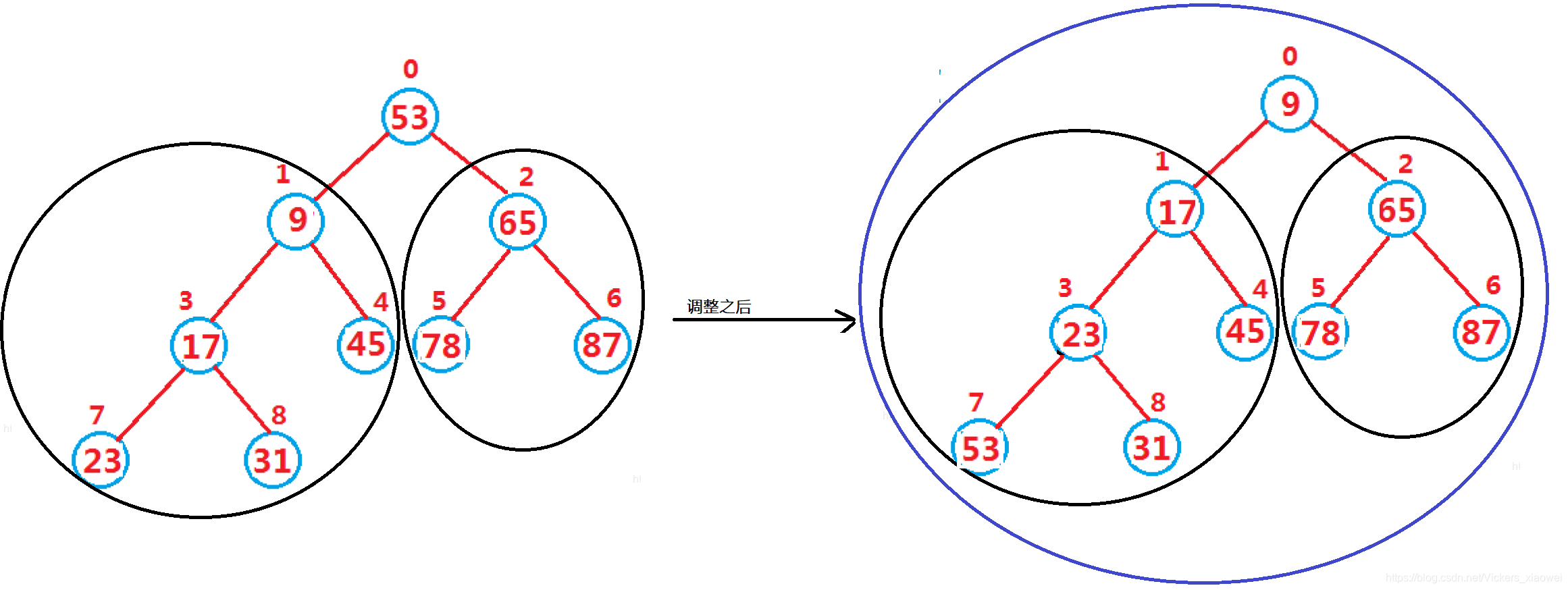
具体的调整方式：向下调整

下标 $p a r e n t$ 从0开始，找到 $p a r e n t$ 的左孩子 $c h i l d = 2 * p a r e n t + 1$ ，如果存在右孩子，让 $c h i l d$ 指向 $l e f t$ 和 $r i g h t$ 中的较小者。
如果 $p a r e n t$ 结点小于等于 $l e f t$ 和 $r i g t h$ 结点的较小者，调整结束，否则将 $p a r e n t$ 元素和较小元素交换，此时，其子树可能不满足堆的性质，则需要继续向下调整。

#include<iostream>
using namespace std;

void AdjustDown(int* arr, int parent, int len)
{
	int child = parent * 2 + 1;

	while (child + 1<len&&child>0)
	{
		if (arr[child + 1]<arr[child])
			child++;
		if (arr[parent]>arr[child])
		{
			swap(arr[parent], arr[child]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
			break;
	}
}
void MakeHeap(int* arr, int len)
{
	for (int i = (len - 2) / 2; i >= 0; i--)
	//最后一个结点的父亲结点就是最后一个非叶子节点
	{
		AdjustDown(arr, i, len);
	}
}
int main()
{
	int arr[] = { 53, 17, 78, 9, 45, 65, 87, 23, 31 };
	int len = sizeof(arr) / sizeof(arr[0]);
	MakeHeap(arr, len);
	for (int i = 0; i < len; i++)
		cout << arr[i] << "  ";
	cout << endl;
	system("pause");
	return 0;
}

在这里插入图片描述

堆的增删

堆的插入

在已经建成的最小堆的后面插入新元素，插入之后，当树中结点不满足堆的性质时，就需要对堆进行重新调整。
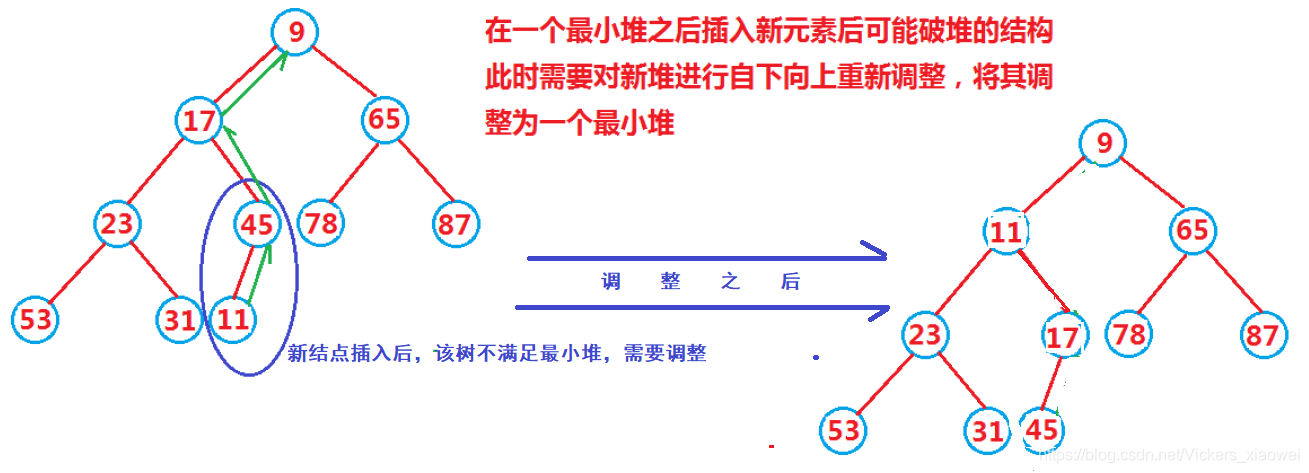
在这里插入图片描述
只有新插入结点至根结点的路径需要调整，而且对于新插入结点的祖先节点来说，已经有序，因此采用自下项上的调整，类似于插入排序。

对于一维数组是不能增删的，所以换用STL的vector来存储一位数组较好。

#include<iostream>
#include<vector>

using namespace std;

void AdjustUp(vector<int>& v)
{
	int insert = v.size() - 1;
	int parent = (insert - 1) / 2;
	while (v[parent] > v[insert]&&parent>=0)
	{
		swap(v[parent], v[insert]);
		insert = parent;
		parent = (insert - 1) / 2;
	}
}
int main()
{
	int arr[] = { 53, 17, 78, 9, 45, 65, 87, 23, 31 };
	int len = sizeof(arr) / sizeof(arr[0]);
	MakeHeap(arr, len);

	vector<int> v(arr, arr + len);
	v.push_back(11);
	AdjustUp(v);

	for (size_t i = 0; i < v.size(); i++)
		cout << v[i] << "  ";
	cout << endl;
	system("pause");
	return 0;
}

堆的删除

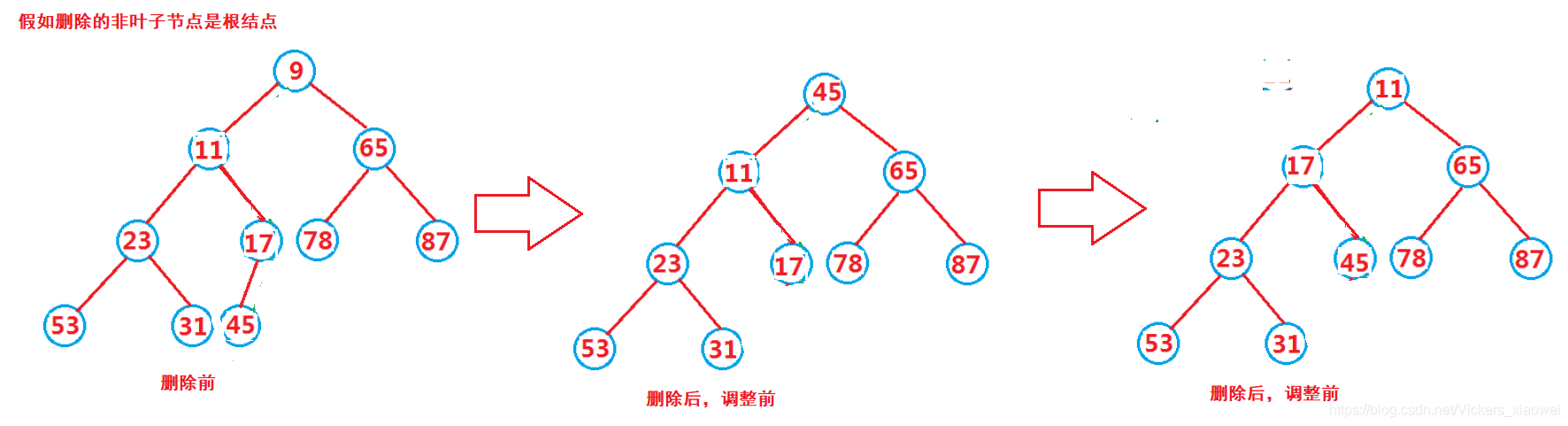
删除叶子结点，将要删除的节点之后的数据向前移动一位，vector尾删。
删除非叶子节点，将vector的最后一个元素替换掉这个非叶子节点元素，vector尾删，可能导致树不满足小堆特性，由替换结点向下调整。

#include<iostream>
#include<vector>

using namespace std;

void AdjustDown(vector<int>& arr, int parent, int len)
{
	int child = parent * 2 + 1;

	while (child + 1<len&&child>0)
	{
		if (arr[child + 1]<arr[child])
			child++;
		if (arr[parent]>arr[child])
		{
			swap(arr[parent], arr[child]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
			break;
	}
}
void MakeHeap(vector<int>& arr, int len)
{
	for (int i = (len - 2) / 2; i >= 0; i--)
	//最后一个结点的父亲结点就是最后一个非叶子节点
	{
		AdjustDown(arr, i, len);
	}
}
void AdjustUp(vector<int>& v)
{
	int insert = v.size() - 1;
	int parent = (insert - 1) / 2;
	while (v[parent] > v[insert]&&parent>=0)
	{
		swap(v[parent], v[insert]);
		insert = parent;
		parent = (insert - 1) / 2;
	}
}
int main()
{
	int arr[] = { 53, 17, 78, 9, 45, 65, 87, 23, 31 };
	int len = sizeof(arr) / sizeof(arr[0]);
	vector<int> v(arr, arr + len);
	MakeHeap(v, len);

	
	v.push_back(11);
	AdjustUp(v);

	int end = v.size() - 1;
	v[0] = v[end];
	v.pop_back();
	AdjustDown(v, 0, end + 1);
	for (size_t i = 0; i < v.size(); i++)
		cout << v[i] << "  ";
	cout << endl;
	system("pause");
	return 0;
}

TopK问题

对于TopK问题，经常面后台开发的人应该不陌生，但是时间久了，自然会遗忘。

假如有100万游戏玩家，如何快速找出当日游戏排名前1000的玩家？
我首先想到的是建大堆，大堆一直保持Top1000的值，可是当第1001个数来了之后和哪一个值进行比较呢？哪一个是1000个数中最小的哪一个？最小值肯定是在叶子节点，那我们总不能再遍历叶子节点查找最小值吧。当树的节点是100万时候，叶子节点大约200个，加上向上调整，插入一个数值大约是220次计算。相比之下，肯定是建小堆，每次只需要跟堆顶元素比较即可，这样插入一个数，大概计算20次，因为堆顶元素是一直是暂时的第1000名。

建小堆：时间效率= $O (n * m)$ （m是层数）

#include<iostream>
#include<vector>
#include<initializer_list>
using namespace std;
class SmallHeal{
public:
	SmallHeal(const initializer_list<int> l)
		:data(l.begin(),l.end())
	{
	}
	void MakeSmallHeap()
	{
		int i =(data.size()-2)>>1;//从最后一个叶子节点的父亲开始，最后一个节点data.size()-1
		while (i>=0)
		{
			AdjustDown(i);
			i--;
		}
	}
	bool Insert(int num)
	{
		if (num > data[0])
			data[0] = num;
		AdjustDown(0);
		return true;
	}
	void Show()
	{
		for (size_t i = 0; i < data.size(); i++)
			cout << data[i] << "    ";
		cout << endl;
	}
private:
	vector<int> data;
	void AdjustDown(int i);
};
void SmallHeal::AdjustDown(int i)
{
	int p = i;
	size_t child = 2 * i + 1;
	while (child<data.size())
	{
		if (child + 1 < data.size())
			child = data[child + 1] < data[child] ? child + 1 : child;//选小孩子
		if (data[child] < data[p])
			swap(data[child], data[p]);
		p = child;
		child = 2 * p + 1;
	}
}

int main()
{
	SmallHeal b{1,10,100,1000,10000};
	b.MakeSmallHeap();
	b.Insert(20);
	b.Insert(200);
	b.Insert(2000);
	b.Show();
	system("pause");
	return 0;
}