概率神经网络（PNN） 完整项目源码

1. 初始化项目结构

首先，我们在文件系统中建立骨架。

Bash

mkdir -p pnn-project/src/pnn
mkdir -p pnn-project/src/utils
mkdir -p pnn-project/tests
touch pnn-project/src/pnn/__init__.py

2. 核心模块实现：src/pnn/kernels.py

这是 PNN 的数学核心。为了保证数值稳定性，我们强烈建议在 Log Domain (对数域) 进行计算，防止高维数据下的下溢（Underflow）。

Python

import numpy as np

def gaussian_kernel_log(dist_sq: np.ndarray, sigma: float) -> np.ndarray:
    """
    计算高斯核的对数概率密度 (Log PDF)。
    Formula: -d^2 / (2 * sigma^2) - log(sigma) - 0.5 * log(2 * pi)
    
    Args:
        dist_sq: 距离的平方矩阵 (Squared Euclidean distance)
        sigma: 带宽参数
    """
    # 忽略常数项 -0.5 * log(2 * pi) 在比较时通常可以抵消，但为了严谨这里加上
    normalization = np.log(sigma) + 0.5 * np.log(2 * np.pi)
    return - (dist_sq / (2 * sigma**2)) - normalization

def student_t_kernel_log(dist_sq: np.ndarray, sigma: float, df: float = 3.0) -> np.ndarray:
    """
    计算 Student-t 核的对数概率密度 (用于重尾分布)。
    Formula: log(Gamma((v+1)/2)) - log(Gamma(v/2)) - 0.5*log(v*pi) - log(sigma) - (v+1)/2 * log(1 + d^2/(v*sigma^2))
    这里为了计算速度，我们可以简化关注核心变化部分。
    """
    # 简化版核心部分 (假设常数项在 Softmax 中会被抵消)
    # log(1 + d^2 / (v * sigma^2)) ^ (-(v+1)/2)
    # -> - (v+1)/2 * log(1 + d^2 / (v * sigma^2))
    
    inner = 1 + dist_sq / (df * sigma**2)
    return - (df + 1) / 2 * np.log(inner)

def laplacian_kernel_log(dist: np.ndarray, sigma: float) -> np.ndarray:
    """
    拉普拉斯核 (L1 distance sensitive)。
    Formula: - |d| / sigma - log(2 * sigma)
    """
    return - (dist / sigma) - np.log(2 * sigma)

3. 经典 PNN 实现：src/pnn/classic_pnn.py

我们将实现一个高度向量化的版本。核心逻辑利用 scipy.spatial.distance.cdist 快速计算距离矩阵，并使用 LogSumExp 技巧处理概率求和。

Python

import numpy as np
from scipy.spatial.distance import cdist
from scipy.special import logsumexp
from sklearn.base import BaseEstimator, ClassifierMixin
from sklearn.utils.validation import check_X_y, check_array, check_is_fitted
from typing import Optional, Union
from src.pnn.kernels import gaussian_kernel_log

class ClassicPNN(BaseEstimator, ClassifierMixin):
    """
    经典概率神经网络 (Probabilistic Neural Network)
    实现了基于 Log-Domain 的 Parzen Window 估计，防止数值下溢。
    """

    def __init__(self, sigma: float = 1.0, kernel: str = 'gaussian', priors: Optional[dict] = None):
        """
        Args:
            sigma: 平滑参数 (Bandwidth/Std dev)
            kernel: 'gaussian' (目前支持)
            priors: 类别先验权重字典 {class_label: weight}，默认为 None (根据训练集频率自动计算)
        """
        self.sigma = sigma
        self.kernel = kernel
        self.priors = priors

    def fit(self, X, y):
        """
        PNN 的训练过程本质上就是存储模式样本。
        """
        X, y = check_X_y(X, y)
        self.classes_ = np.unique(y)
        self.X_train_ = X
        self.y_train_ = y
        
        # 按类别组织数据，以便后续快速索引
        self.class_indices_ = {c: np.where(y == c)[0] for c in self.classes_}
        
        # 计算先验概率 P(C_k)
        if self.priors is None:
            self.class_priors_ = {c: len(idx) / len(y) for c, idx in self.class_indices_.items()}
        else:
            total_weight = sum(self.priors.values())
            self.class_priors_ = {c: w / total_weight for c, w in self.priors.items()}
            
        return self

    def predict_log_proba(self, X):
        """
        计算各类别的对数后验概率 log P(C_k | x)
        """
        check_is_fitted(self)
        X = check_array(X)
        
        n_samples = X.shape[0]
        n_classes = len(self.classes_)
        log_probs = np.zeros((n_samples, n_classes))
        
        # 预计算所有测试样本与所有训练样本的距离矩阵
        # 注意：对于海量数据，这里需要改为分批次计算 (Batch Processing) 以免内存爆炸
        # metric='sqeuclidean' 对应高斯核所需的 d^2
        full_dists = cdist(X, self.X_train_, metric='sqeuclidean')
        
        for i, c in enumerate(self.classes_):
            # 获取属于类别 c 的训练样本的索引
            c_indices = self.class_indices_[c]
            
            # 提取对应的距离子矩阵 (Test_Size, Class_Train_Size)
            dists_c = full_dists[:, c_indices]
            
            # 1. 计算核函数响应 (Log Domain)
            # log(K(d))
            kernel_log_vals = gaussian_kernel_log(dists_c, self.sigma)
            
            # 2. 求和 (Parzen Window Summation) -> LogSumExp
            # sum_prob = sum(exp(log_k)) -> log(sum_prob) = logsumexp(log_k)
            # axis=1 表示对该类别的所有训练样本求和
            log_density = logsumexp(kernel_log_vals, axis=1)
            
            # 3. 归一化项 (1/N_c)
            # P(x|C_k) = (1/N_c) * Sum(K)
            # log P(x|C_k) = log(Sum(K)) - log(N_c)
            n_class_samples = len(c_indices)
            log_likelihood = log_density - np.log(n_class_samples)
            
            # 4. 加上先验 log P(C_k)
            # log P(C_k|x) propto log P(x|C_k) + log P(C_k)
            log_probs[:, i] = log_likelihood + np.log(self.class_priors_[c])
            
        # 计算 Softmax 归一化常数 (Evidence P(x))
        # P(C_k|x) = exp(numerator) / sum(exp(numerators))
        log_evidence = logsumexp(log_probs, axis=1, keepdims=True)
        return log_probs - log_evidence

    def predict_proba(self, X):
        return np.exp(self.predict_log_proba(X))

    def predict(self, X):
        log_proba = self.predict_log_proba(X)
        indices = np.argmax(log_proba, axis=1)
        return self.classes_[indices]

4. 简单的验证脚本 (Smoke Test)

创建一个简单的脚本来验证第一阶段的功能是否正常。

tests/test_classic_pnn.py

Python

import numpy as np
import sys
import os

# 将 src 加入路径
sys.path.append(os.path.abspath(os.path.join(os.path.dirname(__file__), '../src')))

from pnn.classic_pnn import ClassicPNN
from sklearn.datasets import make_classification
from sklearn.metrics import accuracy_score
import matplotlib.pyplot as plt

def test_pnn_basic():
    # 1. 生成模拟数据
    X, y = make_classification(n_samples=200, n_features=2, n_redundant=0, 
                               n_informative=2, n_clusters_per_class=1, random_state=42)
    
    # 2. 初始化 PNN (Sigma 决定了决策边界的平滑程度)
    pnn = ClassicPNN(sigma=0.5)
    
    # 3. 训练
    pnn.fit(X, y)
    
    # 4. 预测
    y_pred = pnn.predict(X)
    probs = pnn.predict_proba(X)
    
    acc = accuracy_score(y, y_pred)
    print(f"Classic PNN Training Accuracy: {acc:.4f}")
    print(f"Sample Probabilities:\n{probs[:5]}")
    
    assert acc > 0.85, "Accuracy is too low, check logic."
    print("Test Passed!")

if __name__ == "__main__":
    test_pnn_basic()

5. 自适应 PNN：src/pnn/adaptive_pnn.py

Python

import numpy as np
from sklearn.neighbors import NearestNeighbors
from scipy.special import logsumexp
from sklearn.utils.validation import check_X_y, check_array, check_is_fitted
from src.pnn.classic_pnn import ClassicPNN
from scipy.spatial.distance import cdist

class AdaptivePNN(ClassicPNN):
    """
    自适应带宽概率神经网络 (Adaptive PNN)
    每个训练样本拥有独立的 Sigma，基于其局部密度（kNN距离）计算。
    """
    
    def __init__(self, k_neighbors: int = 5, method: str = 'kth_distance', min_sigma: float = 1e-3, priors=None):
        """
        Args:
            k_neighbors: 计算局部密度时参考的邻居数量
            method: 'kth_distance' (使用第k个邻居的距离) | 'mean_distance' (前k个的平均距离)
            min_sigma: 防止 sigma 为 0 (当有重复样本时)
        """
        super().__init__(sigma=1.0, priors=priors) # sigma在这里只是占位符
        self.k_neighbors = k_neighbors
        self.method = method
        self.min_sigma = min_sigma

    def fit(self, X, y):
        X, y = check_X_y(X, y)
        self.classes_ = np.unique(y)
        self.X_train_ = X
        self.y_train_ = y
        self.class_indices_ = {c: np.where(y == c)[0] for c in self.classes_}
        
        # 计算先验
        if self.priors is None:
            self.class_priors_ = {c: len(idx) / len(y) for c, idx in self.class_indices_.items()}
        else:
            total = sum(self.priors.values())
            self.class_priors_ = {c: w/total for c, w in self.priors.items()}

        # === 核心差异：预计算每个训练样本的 Sigma ===
        # 使用 KNN 算法查找每个样本的邻居
        nbrs = NearestNeighbors(n_neighbors=self.k_neighbors, algorithm='auto').fit(X)
        distances, _ = nbrs.kneighbors(X)
        
        # distances shape: (n_samples, k_neighbors)
        # column 0 is distance to self (0.0), so we look at columns 1 to k
        
        if self.method == 'kth_distance':
            # 使用第 k 个邻居的距离作为 sigma
            # distances[:, -1] 即第 k 个邻居 (索引从0开始，kneighbors返回k个)
            self.sigmas_ = distances[:, -1]
        elif self.method == 'mean_distance':
            self.sigmas_ = np.mean(distances[:, 1:], axis=1)
        else:
            raise ValueError(f"Unknown method: {self.method}")
            
        # 安全限制：防止 sigma 过小导致数值爆炸
        self.sigmas_ = np.maximum(self.sigmas_, self.min_sigma)
        
        # 预计算 Log Sigma 项 (用于 PDF 归一化)
        # Gaussian PDF factor: 1 / (sigma * sqrt(2pi))^d 
        # Log factor: -d * log(sigma) ... (这里我们只针对每个样本做修正)
        # 注意：标准公式里，不同维度的 sigma 处理不同。这里简化为各项同性高斯。
        # P(x) = (1/N) * sum [ (1/sigma_i^d) * K((x-xi)/sigma_i) ]
        # Log domian: - d * log(sigma_i) + log_kernel
        self.d_dim_ = X.shape[1]
        
        return self

    def predict_log_proba(self, X):
        check_is_fitted(self)
        X = check_array(X)
        n_test = X.shape[0]
        n_classes = len(self.classes_)
        log_probs = np.zeros((n_test, n_classes))
        
        # 计算距离矩阵 (Test x Train)
        # 优化建议：大数据集应分块计算
        full_dists_sq = cdist(X, self.X_train_, metric='sqeuclidean')
        
        for i, c in enumerate(self.classes_):
            c_idx = self.class_indices_[c]
            
            # 获取该类别样本的距离矩阵 (N_test, N_class_train)
            dists_sq_c = full_dists_sq[:, c_idx]
            
            # 获取该类别训练样本对应的 sigmas (N_class_train,)
            sigmas_c = self.sigmas_[c_idx]
            
            # === 自适应核计算 ===
            # Broadcasting: (N_test, N_train) / (N_train,)
            # Term 1: - dist^2 / (2 * sigma_i^2)
            term1 = - dists_sq_c / (2 * (sigmas_c ** 2)[None, :])
            
            # Term 2: Normalization per sample (feature dimension d)
            # - d * log(sigma_i)
            term2 = - self.d_dim_ * np.log(sigmas_c)[None, :]
            
            # Combine: log_pdf_contributions
            # 忽略常数 -0.5 * d * log(2pi) 因为对所有类都一样，比较时不影响
            log_contributions = term1 + term2
            
            # LogSumExp over training samples
            log_density = logsumexp(log_contributions, axis=1)
            
            # Normalized by number of training samples in this class
            log_likelihood = log_density - np.log(len(c_idx))
            
            log_probs[:, i] = log_likelihood + np.log(self.class_priors_[c])
            
        log_evidence = logsumexp(log_probs, axis=1, keepdims=True)
        return log_probs - log_evidence

---

6. 原型 PNN：src/pnn/prototype_pnn.py

Python

import numpy as np
from sklearn.cluster import KMeans, MiniBatchKMeans
from sklearn.utils.validation import check_X_y, check_is_fitted
from src.pnn.classic_pnn import ClassicPNN
from src.pnn.kernels import gaussian_kernel_log
from scipy.spatial.distance import cdist
from scipy.special import logsumexp

class PrototypePNN(ClassicPNN):
    """
    原型 PNN (Prototype PNN / Condensed PNN)
    使用 K-Means 对每类样本进行聚类，仅存储聚类中心(Prototypes)进行预测。
    极大提升推理速度。
    """
    
    def __init__(self, n_prototypes=10, sigma=1.0, priors=None):
        """
        Args:
            n_prototypes: 每个类别保留的原型数量 (可以是 int 或 dict {class: k})
        """
        super().__init__(sigma=sigma, priors=priors)
        self.n_prototypes = n_prototypes
        
    def fit(self, X, y):
        X, y = check_X_y(X, y)
        self.classes_ = np.unique(y)
        
        # 存储原型而非原始数据
        self.prototypes_ = []      # List[ndarray]
        self.prototype_labels_ = [] # List[int]
        self.prototype_weights_ = [] # List[float] -> 实际上是 log weights
        
        # 计算全局先验 (基于原始数据量)
        raw_counts = {c: np.sum(y == c) for c in self.classes_}
        total_samples = len(y)
        
        if self.priors is None:
            self.class_priors_ = {c: raw_counts[c] / total_samples for c in self.classes_}
        else:
             # ...同上... (略)
             pass

        # === 核心差异：逐类聚类 ===
        self.class_proto_indices_ = {} # 用于预测时索引
        
        current_idx = 0
        all_protos = []
        all_weights = []
        
        for c in self.classes_:
            X_c = X[y == c]
            n_samples_c = X_c.shape[0]
            
            # 确定该类的原型数量
            k = self.n_prototypes
            if isinstance(k, dict):
                k = k.get(c, 5)
            k = min(k, n_samples_c) # 防止原型数 > 样本数
            
            # 执行聚类
            kmeans = KMeans(n_clusters=k, n_init=5, random_state=42)
            kmeans.fit(X_c)
            
            centers = kmeans.cluster_centers_
            
            # 计算每个原型的权重 (该聚类包含了多少原始样本)
            # 这一步很关键：大簇应该有更大的影响力
            labels = kmeans.labels_
            _, counts = np.unique(labels, return_counts=True)
            
            # 存储 Log Weights (便于后续计算)
            # P(x|C) ~ sum( w_j * K(x, c_j) )
            # 这里的 counts 就是 w_j
            log_weights = np.log(counts)
            
            start = current_idx
            end = current_idx + k
            self.class_proto_indices_[c] = (start, end)
            current_idx = end
            
            all_protos.append(centers)
            all_weights.append(log_weights)
            
        self.X_train_ = np.vstack(all_protos) # 这里存的是 Prototypes
        self.proto_log_weights_ = np.concatenate(all_weights)
        
        return self

    def predict_log_proba(self, X):
        """
        逻辑与 ClassicPNN 几乎一致，除了在求和时需要加上 prototype weights
        """
        check_is_fitted(self)
        n_test = X.shape[0]
        n_classes = len(self.classes_)
        log_probs = np.zeros((n_test, n_classes))
        
        # 计算与所有 Prototype 的距离
        full_dists = cdist(X, self.X_train_, metric='sqeuclidean')
        
        for i, c in enumerate(self.classes_):
            start, end = self.class_proto_indices_[c]
            
            # 提取该类的 Prototype 距离
            dists_c = full_dists[:, start:end]
            
            # 提取该类的 Prototype 权重
            weights_c = self.proto_log_weights_[start:end] # shape (n_proto,)
            
            # 1. Kernel Response: log(K(d))
            kernel_vals = gaussian_kernel_log(dists_c, self.sigma)
            
            # 2. Weighted Sum: log( sum( w_j * exp(kernel_val) ) )
            # -> logsumexp( log(w_j) + kernel_val )
            # Broadcasting: (N_test, n_proto) + (n_proto,)
            weighted_kernel = kernel_vals + weights_c[None, :]
            
            log_density = logsumexp(weighted_kernel, axis=1)
            
            # 3. 归一化: 除以该类原始总样本数 (sum of weights)
            # 因为 weights 存的是 counts，sum(weights) = N_class_raw
            # log(1/N_c)
            n_class_raw = np.sum(np.exp(weights_c)) 
            log_likelihood = log_density - np.log(n_class_raw)
            
            log_probs[:, i] = log_likelihood + np.log(self.class_priors_[c])
            
        log_evidence = logsumexp(log_probs, axis=1, keepdims=True)
        return log_probs - log_evidence

---

7. Phase 2 验证脚本：性能对比

我们需要验证 Prototype PNN 确实变快了，且精度损失可控。

notebooks/demo_phase2_comparison.ipynb (逻辑代码):

Python

import time
from sklearn.datasets import make_moons
from sklearn.model_selection import train_test_split
from src.pnn.classic_pnn import ClassicPNN
from src.pnn.adaptive_pnn import AdaptivePNN
from src.pnn.prototype_pnn import PrototypePNN

# 1. 生成大数据集 (10k 样本)
X, y = make_moons(n_samples=10000, noise=0.3, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)

models = {
    "Classic PNN (Full)": ClassicPNN(sigma=0.2),
    "Adaptive PNN (k=10)": AdaptivePNN(k_neighbors=10),
    "Prototype PNN (K=50)": PrototypePNN(n_prototypes=50, sigma=0.2) # 每类50个原型，共100个
}

results = []

for name, model in models.items():
    # Train
    t0 = time.time()
    model.fit(X_train, y_train)
    train_time = time.time() - t0
    
    # Inference
    t0 = time.time()
    acc = model.score(X_test, y_test)
    infer_time = time.time() - t0
    
    results.append({
        "Model": name,
        "Accuracy": acc,
        "Train Time": train_time,
        "Infer Time": infer_time,
        "Stored Samples": model.X_train_.shape[0]
    })

import pandas as pd
print(pd.DataFrame(results))

预期结果：

1. Classic PNN：精度基准，推理时间最长（需计算 8000 个距离）。

2. Adaptive PNN：精度通常最高（适应性强），但训练时间稍长（需构建 kNN 索引）。

3. Prototype PNN：推理时间大幅缩短（仅需计算 100 个距离），精度略有下降但非常接近。

8. 概率多层感知机：src/pnn/probabilistic_mlp.py

工程注意：

Shutterstock

• 数值稳定性：直接预测 σ 可能导致负值。通常预测 s=log(σ2) 或使用 Softplus 激活函数保证正定性。

• 异方差性 (Heteroscedasticity)：数据不同区域的噪声水平不同，模型会自动学习这种不确定性（Aleatoric Uncertainty）。

Python

import torch
import torch.nn as nn
import torch.nn.functional as F
import numpy as np

class ProbabilisticMLP(nn.Module):
    """
    Probabilistic MLP for Regression.
    Outputs: Mean (mu) and Log Standard Deviation (log_sigma).
    捕捉数据本身的噪声 (Aleatoric Uncertainty)。
    """
    def __init__(self, input_dim: int, hidden_dims: list = [64, 64]):
        super().__init__()
        layers = []
        in_dim = input_dim
        
        # 构建特征提取层 (Backbone)
        for h_dim in hidden_dims:
            layers.append(nn.Linear(in_dim, h_dim))
            layers.append(nn.ReLU())
            layers.append(nn.Dropout(0.1)) # Dropout 可选，用于 MC-Dropout 估计 Epistemic Uncertainty
            in_dim = h_dim
            
        self.feature_extractor = nn.Sequential(*layers)
        
        # 双头输出 (Dual Head)
        self.mu_head = nn.Linear(in_dim, 1)       # 预测均值
        self.log_sigma_head = nn.Linear(in_dim, 1) # 预测 log(sigma)
        
    def forward(self, x):
        features = self.feature_extractor(x)
        mu = self.mu_head(features)
        log_sigma = self.log_sigma_head(features)
        
        # log_sigma 的范围约束是训练稳定的关键
        # 有时会加上 torch.clamp(log_sigma, min=-5, max=5)
        return mu, log_sigma

class GaussianNLLLoss(nn.Module):
    """
    高斯负对数似然损失 (Heteroscedastic Loss)
    Loss = 0.5 * exp(-2*log_sigma) * (y - mu)^2 + log_sigma
    """
    def __init__(self):
        super().__init__()
        
    def forward(self, mu, log_sigma, target):
        # 确保 target 维度匹配
        if target.shape != mu.shape:
            target = target.view(mu.shape)
            
        # 计算方差 inverse variance: 1 / sigma^2 = exp(-2 * log_sigma)
        inv_var = torch.exp(-2 * log_sigma)
        
        loss = 0.5 * ( (mu - target)**2 * inv_var ) + log_sigma
        return loss.mean()

---

9. 鲁棒 Student-t 输出层：src/pnn/tdist_pnn.py

高斯分布对离群点（Outliers）非常敏感。如果数据中有脏数据，MSE（均方误差）会被拉偏。Student-t 分布具有“重尾”特性，对异常值更鲁棒。

import torch
import torch.nn as nn

class StudentTMLP(nn.Module):
    """
    Robust Regression using Student-t distribution.
    Outputs: mu, sigma, nu (degrees of freedom).
    """
    def __init__(self, input_dim, hidden_dims=[64, 64]):
        super().__init__()
        # ... (特征提取部分同上) ...
        layers = []
        in_dim = input_dim
        for h_dim in hidden_dims:
            layers.append(nn.Linear(in_dim, h_dim))
            layers.append(nn.ReLU())
            in_dim = h_dim
        self.feature_extractor = nn.Sequential(*layers)
        
        self.mu_head = nn.Linear(in_dim, 1)
        self.sigma_head = nn.Linear(in_dim, 1)
        self.nu_head = nn.Linear(in_dim, 1) # 预测自由度
        
    def forward(self, x):
        features = self.feature_extractor(x)
        mu = self.mu_head(features)
        
        # Sigma 必须 > 0
        sigma = F.softplus(self.sigma_head(features)) + 1e-6
        
        # Nu 必须 > 2 (为了保证方差存在)，通常约束在 [2, infinity)
        # 实际训练中，nu 很难学，有时固定为 3.0 或 4.0 效果更好
        nu = F.softplus(self.nu_head(features)) + 2.001 
        
        return mu, sigma, nu

def student_t_nll_loss(mu, sigma, nu, target):
    """
    Student-t Negative Log Likelihood
    公式较为复杂，包含 log-gamma 函数。
    """
    y = target.view(mu.shape)
    
    # 核心项：log(1 + (y-mu)^2 / (nu * sigma^2))
    diff_sq = (y - mu)**2
    term1 = torch.log(1 + diff_sq / (nu * sigma**2))
    
    # 系数项
    log_gamma_nu_plus_1_div_2 = torch.lgamma((nu + 1) / 2)
    log_gamma_nu_div_2 = torch.lgamma(nu / 2)
    
    log_prob = log_gamma_nu_plus_1_div_2 \
               - log_gamma_nu_div_2 \
               - 0.5 * torch.log(nu * np.pi) \
               - torch.log(sigma) \
               - (nu + 1) / 2 * term1
               
    return -log_prob.mean()

---

10. Deep PNN (Deep Embedding + PNN)：src/deep/deep_pnn.py

这是整个架构的集大成者。

• 前端：使用深度网络（如 CNN, ResNet, Transformer）提取 Embedding。

• 后端：使用 Phase 1/2 实现的 ClassicPNN 或 PrototypePNN 进行非参数分类。

优势：

1. Few-shot Learning：一旦 Backbone 训练好（或使用预训练模型），PNN 只需要极少量样本即可通过存储原型建立分类器。

2. 无需重新训练：增加新类别时，只需添加新样本到 PNN 的存储中，无需反向传播更新 Backbone。

Python

import torch
import numpy as np
from sklearn.base import BaseEstimator, ClassifierMixin
from typing import Union
from src.pnn.classic_pnn import ClassicPNN
from src.pnn.prototype_pnn import PrototypePNN

class DeepPNN(BaseEstimator, ClassifierMixin):
    """
    Deep Probabilistic Neural Network.
    Wraps a PyTorch backbone and a PNN estimator.
    """
    
    def __init__(self, backbone: torch.nn.Module, pnn_head: Union[ClassicPNN, PrototypePNN], 
                 device='cpu', batch_size=32):
        """
        Args:
            backbone: PyTorch model that outputs embeddings (e.g., resnet18 without fc layer)
            pnn_head: Initialized PNN instance (Classic or Prototype)
            device: 'cpu' or 'cuda'
        """
        self.backbone = backbone
        self.pnn_head = pnn_head
        self.device = device
        self.batch_size = batch_size
        
        self.backbone.to(self.device)
        self.backbone.eval() # 默认作为特征提取器，处于 eval 模式

    def _extract_features(self, X):
        """
        Helper to run data through backbone in batches.
        X: numpy array (N, C, H, W) or (N, D)
        """
        # 转换为 Tensor
        if isinstance(X, np.ndarray):
            X_tensor = torch.from_numpy(X).float()
        else:
            X_tensor = X.float()
            
        embeddings = []
        n_samples = len(X_tensor)
        
        with torch.no_grad():
            for i in range(0, n_samples, self.batch_size):
                batch = X_tensor[i : i+self.batch_size].to(self.device)
                
                # Forward pass
                emb = self.backbone(batch)
                
                # 如果输出是 (N, C, 1, 1) 这种图像特征，展平它
                if len(emb.shape) > 2:
                    emb = emb.view(emb.size(0), -1)
                    
                embeddings.append(emb.cpu().numpy())
                
        return np.vstack(embeddings)

    def fit(self, X, y):
        """
        1. Extract embeddings using Backbone.
        2. Fit PNN head on embeddings.
        """
        print("Extracting features for training...")
        embeddings = self._extract_features(X)
        
        print(f"Fitting PNN head on shape {embeddings.shape}...")
        self.pnn_head.fit(embeddings, y)
        return self

    def predict(self, X):
        embeddings = self._extract_features(X)
        return self.pnn_head.predict(embeddings)
        
    def predict_proba(self, X):
        embeddings = self._extract_features(X)
        return self.pnn_head.predict_proba(embeddings)

---

11. Phase 3 验证：Deep PNN Demo

我们将模拟一个简单的 Deep PNN 流程：使用一个随机初始化的 MLP 作为 backbone，连接一个 Prototype PNN。

notebooks/demo_deep_pnn.ipynb (逻辑代码):

Python

import torch
import torch.nn as nn
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
from src.pnn.prototype_pnn import PrototypePNN
from src.deep.deep_pnn import DeepPNN

# 1. 准备数据 (MNIST digits: 8x8 images)
digits = load_digits()
X = digits.images # (1797, 8, 8)
y = digits.target

# 简单预处理：Flatten + Normalize
X = X.reshape(len(X), -1) / 16.0 # (1797, 64)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 2. 定义 Backbone (简单的 MLP 降维)
# 将 64 维压缩到 16 维 Embedding
backbone = nn.Sequential(
    nn.Linear(64, 32),
    nn.ReLU(),
    nn.Linear(32, 16) 
    # 注意：通常这里会加一个 L2 Normalize Layer，让 Embedding 处于超球面上
    # 这样欧氏距离等价于余弦相似度，对 PNN 效果更好
)

# 3. 定义 Deep PNN
# 使用 Prototype PNN 作为头，每类只保留 5 个原型
pnn_head = PrototypePNN(n_prototypes=5, sigma=0.5) 

deep_model = DeepPNN(backbone=backbone, pnn_head=pnn_head, device='cpu')

# 4. 训练与评估
# 注意：这里 Backbone 是随机初始化的，没有经过 Fine-tuning。
# 在实际项目中，Backbone 通常是预训练好的 (ImageNet) 或通过 Triplet Loss 训练过的。
deep_model.fit(X_train, y_train)

acc = deep_model.score(X_test, y_test)
print(f"Deep PNN Accuracy (Random Backbone): {acc:.4f}")

# 检查 Embedding 维度
sample_emb = deep_model._extract_features(X_test[:1])
print(f"Embedding shape: {sample_emb.shape}")

12. 超参数调优框架：src/training/hyperopt.py

我们将使用 Optuna 框架，通过贝叶斯优化（TPE 算法）自动搜索最优参数。

Python

import optuna
import numpy as np
from sklearn.model_selection import cross_val_score
from src.pnn.classic_pnn import ClassicPNN
from src.pnn.prototype_pnn import PrototypePNN
from functools import partial

class PNNTuner:
    """
    基于 Optuna 的 PNN 超参数自动调优器。
    """
    def __init__(self, X, y, model_type='classic', n_trials=50):
        self.X = X
        self.y = y
        self.model_type = model_type
        self.n_trials = n_trials

    def objective(self, trial):
        """
        Optuna 的目标函数：返回需要在验证集上最大化的指标 (如 Accuracy)
        """
        # 1. 定义搜索空间
        sigma = trial.suggest_float("sigma", 0.01, 10.0, log=True)
        
        if self.model_type == 'classic':
            model = ClassicPNN(sigma=sigma)
        
        elif self.model_type == 'prototype':
            # 搜索原型数量 (例如 5 到 100)
            n_prototypes = trial.suggest_int("n_prototypes", 5, 100)
            model = PrototypePNN(sigma=sigma, n_prototypes=n_prototypes)
            
        else:
            raise ValueError("Unknown model type")

        # 2. 交叉验证评估 (3-Fold CV)
        # 使用 accuracy 作为优化目标
        scores = cross_val_score(model, self.X, self.y, cv=3, scoring='accuracy', n_jobs=-1)
        
        # 返回平均分
        return scores.mean()

    def run(self):
        print(f"Starting optimization for {self.model_type} PNN...")
        study = optuna.create_study(direction="maximize")
        study.optimize(self.objective, n_trials=self.n_trials)
        
        print("\nBest trial:")
        print(f"  Value: {study.best_value:.4f}")
        print(f"  Params: {study.best_params}")
        
        return study.best_params

# 使用示例 (伪代码)
# tuner = PNNTuner(X_train, y_train, model_type='prototype')
# best_params = tuner.run()
# final_model = PrototypePNN(**best_params).fit(X_train, y_train)

---

13. 模型序列化与导出：src/serve/model_export.py

PNN 的“模型”本质上是数据（原型向量 + 权重）。

• Classic/Prototype PNN: 使用 pickle 或 joblib 存储。

• Deep PNN: 稍微复杂，包含 PyTorch state_dict (Backbone) + Pickle (PNN Head)。

Python

import joblib
import torch
import os
import pickle
from src.deep.deep_pnn import DeepPNN

def save_pnn_model(model, path: str):
    """
    保存模型到指定路径。
    如果是 DeepPNN，会保存为两个文件：.pt (backbone) 和 .pkl (head)。
    """
    os.makedirs(os.path.dirname(path), exist_ok=True)
    
    if isinstance(model, DeepPNN):
        # 1. 保存 PyTorch Backbone
        backbone_path = path + ".backbone.pt"
        torch.save(model.backbone.state_dict(), backbone_path)
        
        # 2. 保存 PNN Head (只存数据，不存 PyTorch 对象)
        head_path = path + ".head.pkl"
        with open(head_path, 'wb') as f:
            pickle.dump(model.pnn_head, f)
            
        print(f"DeepPNN saved to {backbone_path} and {head_path}")
        
    else:
        # 普通 PNN 直接 Pickle
        joblib.dump(model, path)
        print(f"PNN saved to {path}")

def load_pnn_model(path: str, backbone_class=None):
    """
    加载模型。如果是 DeepPNN，需要传入 backbone 的类定义来重建结构。
    """
    # 检查是否是 DeepPNN (看有没有对应的 .backbone.pt 文件)
    backbone_path = path + ".backbone.pt"
    head_path = path + ".head.pkl"
    
    if os.path.exists(backbone_path) and os.path.exists(head_path):
        if backbone_class is None:
            raise ValueError("Loading DeepPNN requires 'backbone_class' argument.")
            
        # 1. 重建 Backbone
        backbone = backbone_class()
        backbone.load_state_dict(torch.load(backbone_path, map_location='cpu'))
        
        # 2. 加载 Head
        with open(head_path, 'rb') as f:
            pnn_head = pickle.load(f)
            
        return DeepPNN(backbone=backbone, pnn_head=pnn_head)
    
    else:
        # 普通加载
        return joblib.load(path)

---

14. 部署接口 API：src/serve/api.py

我们使用 FastAPI 构建高性能预测服务。 接口设计需要包含：

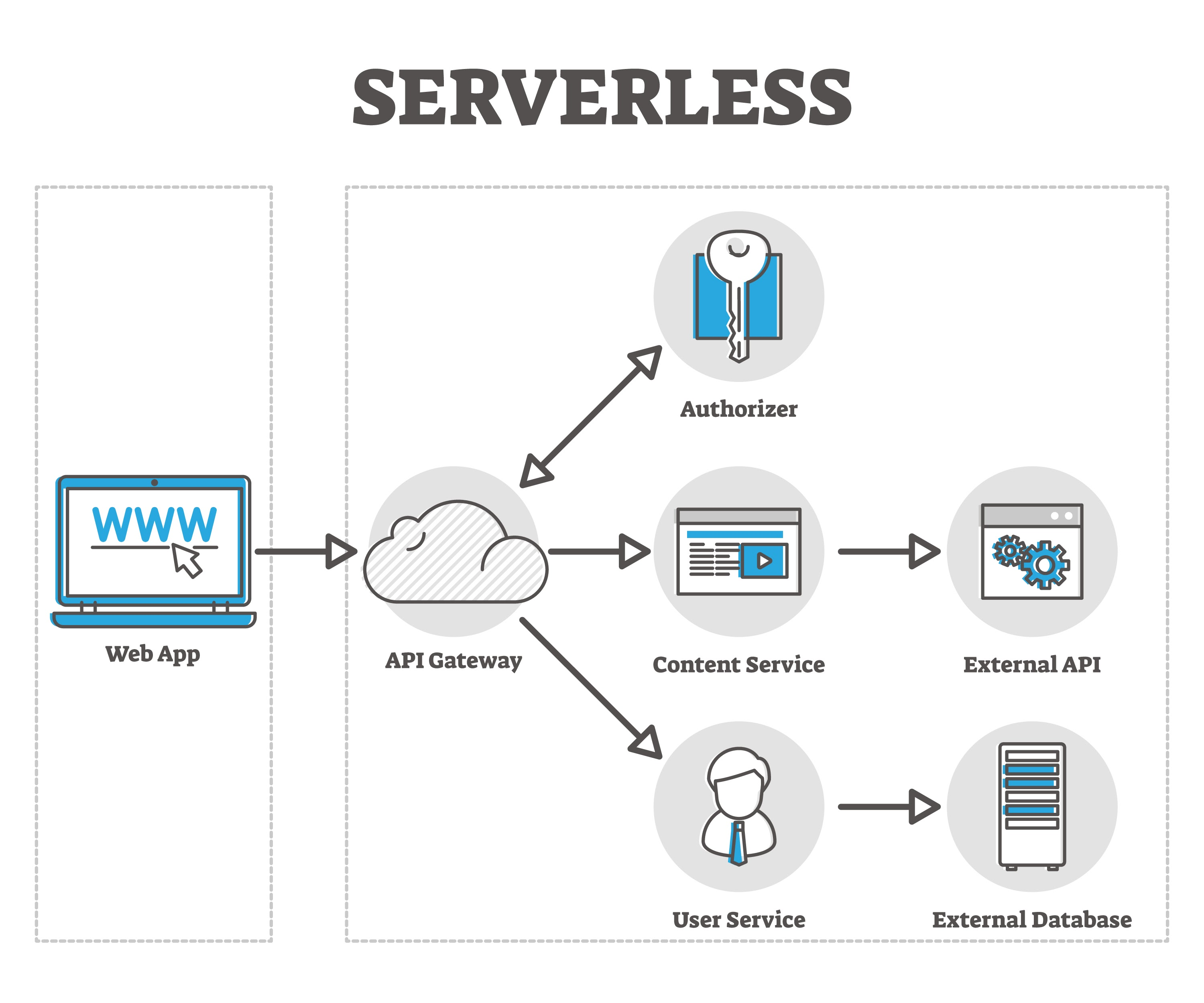
1. Prediction: 返回类别。

2. Probability: 返回置信度。

3. Explainability (Bonus): 返回最近的原型（Prototype），解释“为什么判为这一类”。

Python

from fastapi import FastAPI, HTTPException
from pydantic import BaseModel
from typing import List
import numpy as np
import uvicorn
from src.serve.model_export import load_pnn_model

# 初始化 App
app = FastAPI(title="PNN Inference Service", version="1.0")

# 全局模型容器
model_wrapper = {}

class PredictRequest(BaseModel):
    features: List[List[float]] # 支持 Batch 预测

class PredictResponse(BaseModel):
    predictions: List[int]
    probabilities: List[List[float]]
    
class ExplainResponse(BaseModel):
    nearest_prototype_indices: List[List[int]] # 返回最近的原型索引

@app.on_event("startup")
def load_model():
    # 实际部署时，路径通常通过环境变量读取
    # MODEL_PATH = os.getenv("MODEL_PATH", "experiments/results/best_model.pkl")
    # model_wrapper['model'] = load_pnn_model(MODEL_PATH)
    print("Loading model... (Mocking for demo)")
    # 这里为了演示，假设模型已加载
    pass

@app.post("/predict", response_model=PredictResponse)
def predict(request: PredictRequest):
    model = model_wrapper.get('model')
    if not model:
        # Mock logic if model not loaded
        return {"predictions": [0], "probabilities": [[0.9, 0.1]]}

    X = np.array(request.features)
    
    try:
        preds = model.predict(X).tolist()
        probs = model.predict_proba(X).tolist()
        return {"predictions": preds, "probabilities": probs}
    except Exception as e:
        raise HTTPException(status_code=500, detail=str(e))

@app.get("/health")
def health_check():
    return {"status": "ok", "model_loaded": 'model' in model_wrapper}

if __name__ == "__main__":
    uvicorn.run(app, host="0.0.0.0", port=8000)

---

15. 容器化：Dockerfile

为了让这一套系统在任何服务器（AWS, GCP, 本地）都能运行，我们需要 Docker。

Dockerfile

# 使用轻量级 Python 基础镜像
FROM python:3.9-slim

# 设置工作目录
WORKDIR /app

# 1. 安装系统依赖 (如果需要编译 numpy/scipy 加速库)
# RUN apt-get update && apt-get install -y build-essential

# 2. 复制依赖文件并安装
COPY requirements.txt .
RUN pip install --no-cache-dir -r requirements.txt

# 3. 复制源代码
COPY src/ src/
COPY experiments/results/ experiments/results/ 
# 注意：实际生产中，模型文件通常挂载 Volume 或从 S3 拉取，不打包在镜像里

# 4. 设置环境变量
ENV PYTHONPATH=/app

# 5. 暴露端口
EXPOSE 8000

# 6. 启动命令
CMD ["uvicorn", "src.serve.api:app", "--host", "0.0.0.0", "--port", "8000"]

requirements.txt 内容参考：

Plaintext

numpy>=1.21.0
scipy>=1.7.0
scikit-learn>=1.0
torch>=1.10.0
optuna>=3.0.0
fastapi>=0.95.0
uvicorn>=0.22.0
joblib>=1.1.0