
🎬 GitHub:Vect的代码仓库
1. 把字符串转成整数(atoi)
把字符串转成整数(atoi)
根据题目要求,把字符串转成32位有符号整数,需要考虑下列情况:
1. 首部空格: 直接删除
2. 符号位: 三种情况, + - “无符号”, 可以创建一个sign变量保存符号位,返回前判断一下正负就好
3. 非数字字符: 遇到第一个非数字字符就停止
4. 数字字符:
- 字符转数字:这个数字的
ascii- 0对应的ASCII - 数字拼接:转成十进制数,假设当前位字符是 c c c,当前位数字是 x x x,相加结果是 r e s res res,那么就有如下公式: r e s = 10 × r e s + x res = 10 \times res + x res=10×res+x
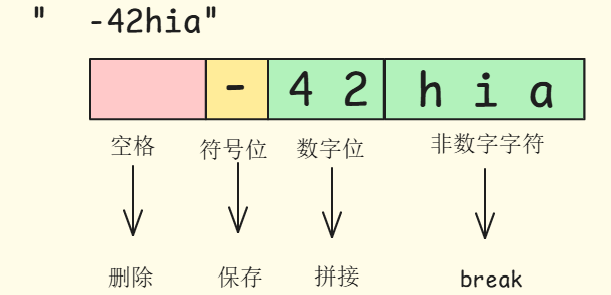
因为我们是从左到右按十进制把数字一位一位“接在末尾地构造整数。十进制是以 10 为底的位权制:每往左一位,权值就×10。因此当读到下一位数字x(0~9)时,现有结果 res 里所有位都要整体左移一位(位权×10),再把新的一位x加到个位上
如图所示:
- 越界检查:
[
−
2
31
,
2
31
−
1
]
[-2^{31}, 2^{31} - 1 ]
[−231,231−1],即是[-2,147,483,648,2,147,483,647]
我们在每轮数字拼接前都要判断 r e s res res在拼接后是否超过2,147,483,647,若超过边界就加上符号位直接返回即可
这里讨论一下越界情况:- r e s × 10 > 2 , 147 , 483 , 647 res \times 10 > 2,147,483,647 res×10>2,147,483,647,拼接的时候越界
-
r
e
s
=
2
,
147
,
483
,
640
,
r
e
s
+
x
>
2
,
147
,
483
,
647
res = 2,147,483,640 ,res + x > 2,147,483,647
res=2,147,483,640,res+x>2,147,483,647,这种情况
x
=
8
或者
x
=
9
x=8 或者 x=9
x=8或者x=9
解释一下:
r e s res res每次都要 × 10 \times 10 ×10,要确保 r e s × 10 res\times 10 res×10之后不能越界
r e s = 214748364 res = 214748364 res=214748364时, r e s × 10 = 214748640 res \times 10=214748640 res×10=214748640,没有越界
现在要加上数字位x,也要保证不能越界,所以 x < = 7 x<=7 x<=7
总结一下思路:
- 遇到空格删除
- 遇到符号保留
- 遇到数字进行拼接,并检查边界
- 遇到第一个非数字字符,
break
代码实现:
class Solution {
public:
int myAtoi(string str) {
int length = str.size(); // 原字符串长度
int idx = 0; // 当前扫描位置
int res = 0; // 逐位累积出来的“绝对值部分”(不带符号)
int sign = 1; // 记录符号,默认正
int border = INT_MAX / 10; // 溢出预判用的安全边界(214748364):
// 1. 处理空格和符号
// 跳过前导空格;这里仅忽略 ' ',不处理 \t \n 等
while (idx < length && str[idx] == ' ') ++idx;
// 如果全是空格,直接返回 0
if (idx == length) return 0;
// 读取一个可选符号位
if (str[idx] == '+' || str[idx] == '-') {
sign = (str[idx] == '-') ? -1 : 1; // 记录符号
++idx; // 移过符号
}
// 2. 拼接数字
// 从 idx 开始,连续读取数字字符;遇到第一个非数字就停止
for(int j = idx; j < length; j++){
// 非数字字符:结束数字段(只读第一段连续数字)
if(str[j] < '0' || str[j] > '9') break;
// 溢出预判
// res 代表当前已累积的正数部分,准备并入下一位 str[j]
// 两种会超上界(INT_MAX=2147483647)的情况:
// 1) res > 214748364(即 border),res*10 一定超
// 2) res == 214748364 且下一位 > 7(INT_MAX % 10),res*10 + x 会超
if(res > border || (res == border && str[j] > '7'))
// 一旦会超:根据 sign 返回相应端点(正:INT_MAX;负:INT_MIN)
return sign == 1 ? INT_MAX : INT_MIN;
// 安全:把当前位并入(十进制每进一位×10,再加本位数字)
res = 10 * res + (str[j] - '0');
}
// 乘上符号返回结果
return sign * res;
}
};
2. 字符串相加
字符串相加
思路:用一个新的数组存放相加后的结果,从后往前遍历两个字符串,将检索到的数字字符分别转换成int类型后,再相加,此时会出现两种情况:
1. 进位,保留个位数字,存到数组里,下一位多加1
2. 不进位,直接将结果存到数组
加完之后要判断最高位是否还要进位
最后逆转数组即可
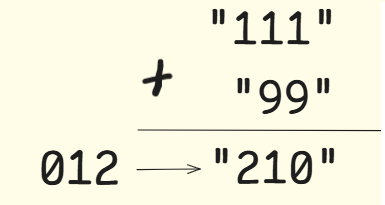
代码实现:
class Solution {
public:
// 思路:模拟竖式加法。从两个字符串末尾(最低位)开始逐位相加
// 用up记录进位,把每一轮的个位先 push 到结果字符串尾部
// 循环结束后若仍有进位再补 '1',最后整体 reverse 得到高位在前的正确结果
string addStrings(std::string num1, std::string num2) {
string numArr; // 结果暂存区:按低位→高位的顺序依次push字符 最终再反转
int up = 0; // 进位
// i/j 当前处理的位 从最右端开始
int i = num1.size() - 1;
int j = num2.size() - 1;
// 任一字符串还有未处理的位就继续
// 不用拆两段剩余位循环
while (i >= 0 || j >= 0) {
// 取 num1 当前位数字 a 若越界则取 0
int a = (i >= 0) ? (num1[i] - '0') : 0;
// 取 num2 当前位数字 b 若越界则取 0
int b = (j >= 0) ? (num2[j] - '0') : 0;
// 本轮求和
int ones = a + b + up;
// 更新本轮进位:十进制进位等于对 10 取整除(0 或 1)
up = ones / 10;
// 本位应当写入的“个位数”是对 10 取模的结果
ones %= 10;
// 把本位结果转成字符追加到 numArr 尾部
numArr.push_back('0' + ones);
--i;
--j;
}
// 所有位处理完毕后,如果还有进位(如 999 + 1),需要再补一个最高位 '1'
if (up) {
numArr.push_back('1');
}
// 当前 numArr 为逆序,反转成高位在前
reverse(numArr.begin(), numArr.end());
return numArr;
}
};
3. 字符串相乘
字符串相乘
思路和字符串相加类似:
- 开一个
ansArr数组存储相乘的结果
数组开多大?num1是 m m m大小,num2是 n n n大小
开 m + n m+n m+n(最大) 最小呢? m + n − 1 m+n-1 m+n−1
如图所示:
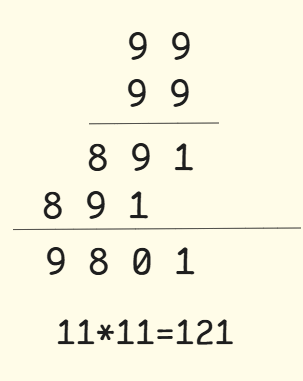
- 按照竖式乘法的习惯,
i是num1的索引,j是num2的索引,先固定j,从后往前遍历num1[i]与num2[j]分贝相乘,相乘结果有两种:
- 不用进位,结果存在
ansArr[i+j+1] - 需要进位,十位结果存在
ansArr[i+j]
- 不断循环,直到两个数组都遍历完成
- 判断是否有前导0,将数字转为字符串输出
具体过程如图所示:
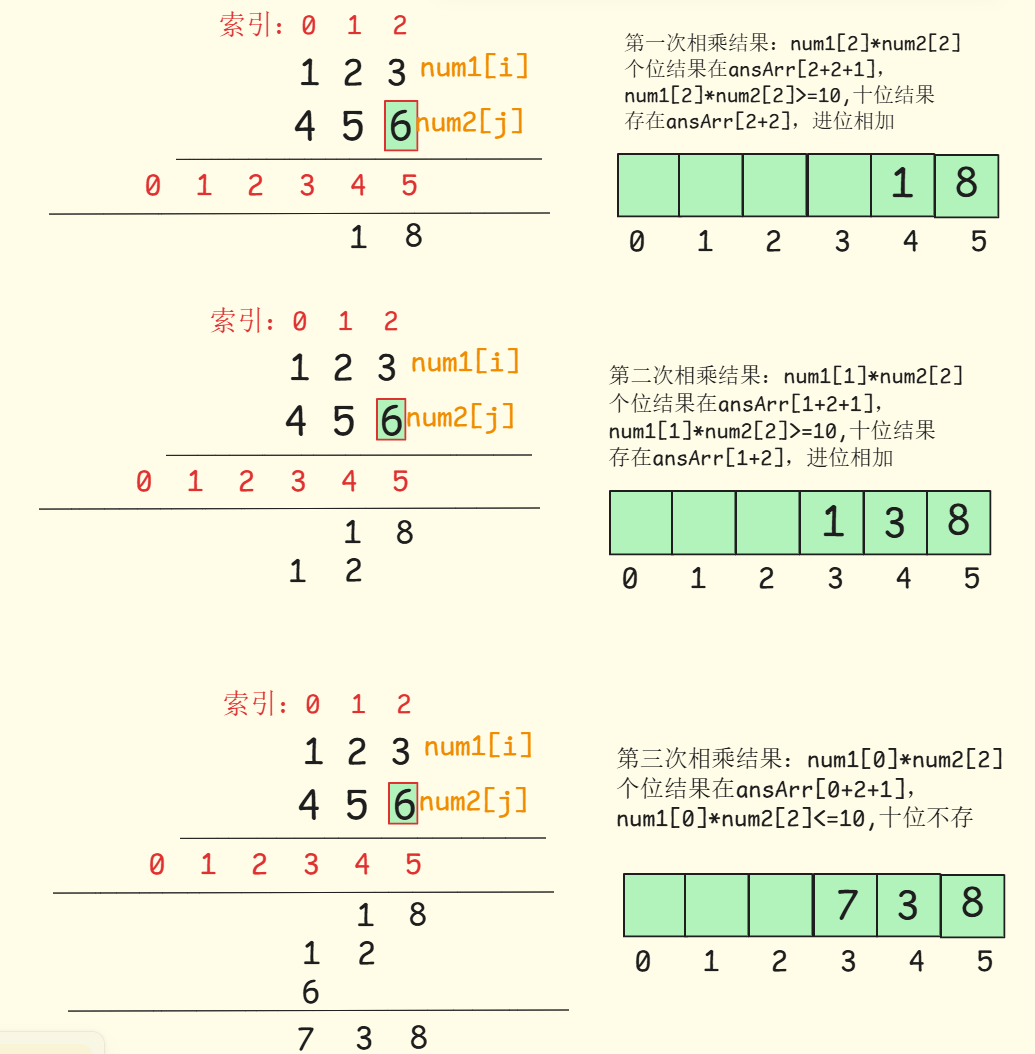
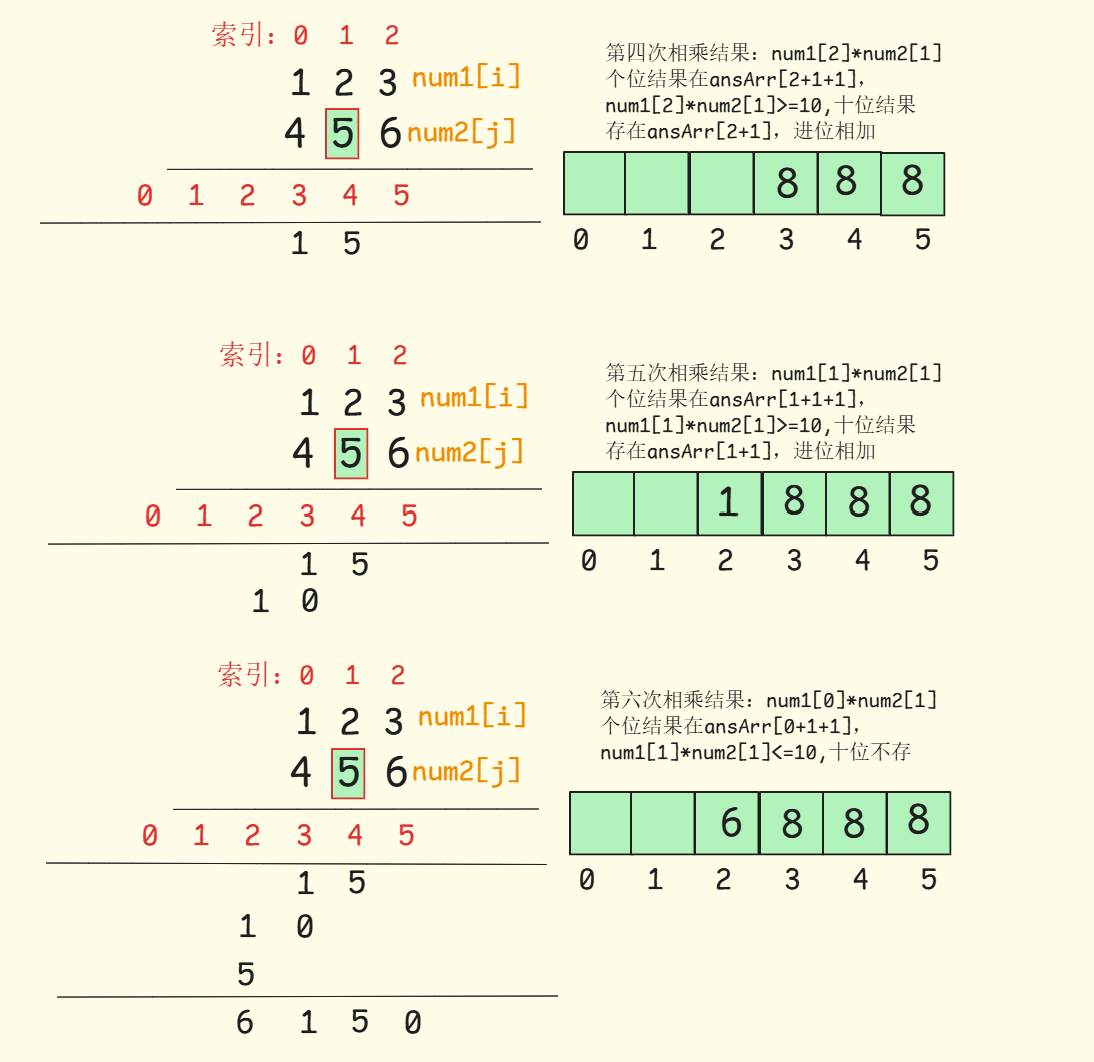
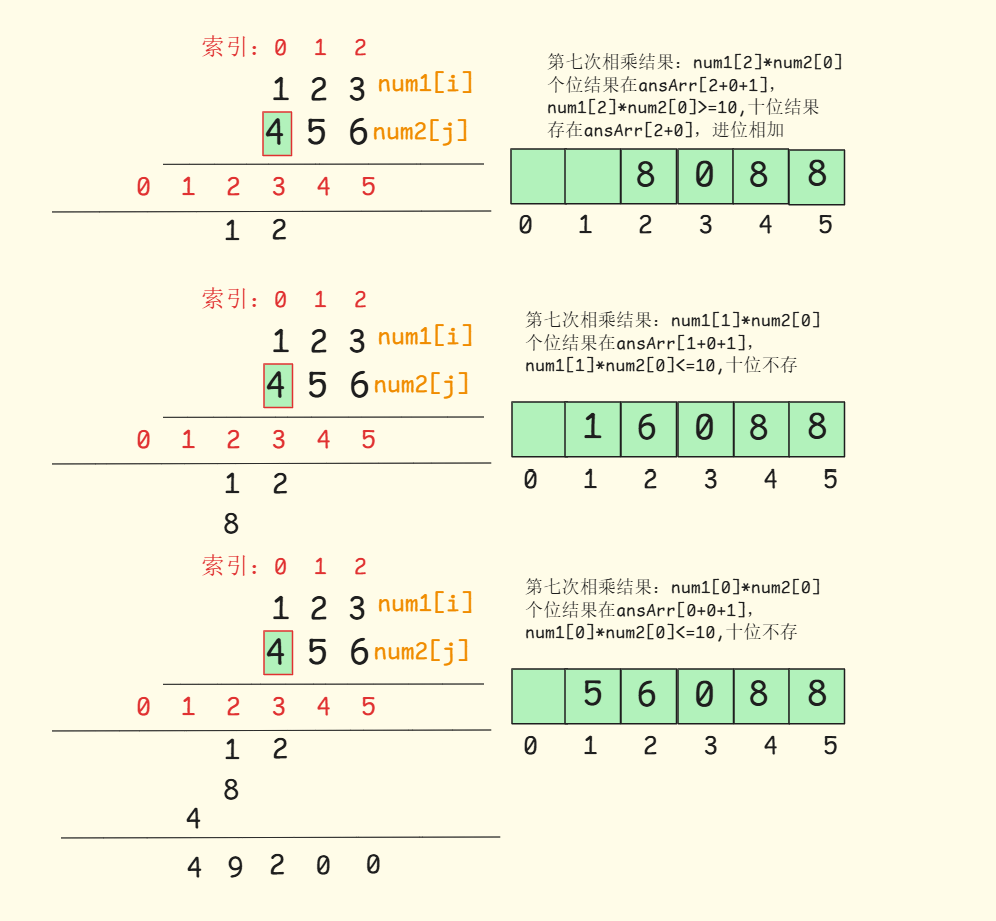
本质就是做了三次加法:
738
+
6150
+
49200
738+6150+49200
738+6150+49200
代码实现:
class Solution {
public:
string multiply(string num1, string num2) {
if(num1 == "0" || num2 == "0") return "0"; // 0*任何数都为0
int sizeNum1 = num1.size();
int sizeNum2 = num2.size();
// 结果最多为 m+n 位,因此开一个 m+n 的整型桶数组存每一位(高位在前,低位在后)
vector<int> ansArr(sizeNum1 + sizeNum2, 0); // 存相乘结果的数组
int res = 0; // 暂存“当前位置已有值 + 本次乘积”的和(便于取个位与进位)
// i/j 当前处理的位置,从最右端(最低位)开始向左
int i = sizeNum1 - 1, j = sizeNum2 - 1;
// 双层循环:num1 的每一位 × num2 的每一位
for(; i >= 0; i--){
int x = num1[i] - '0';
for(j = sizeNum2 - 1; j >= 0; j--){ // 每次外层循环都把 j 复位到末尾
int y = num2[j] - '0';
/* 对齐思路:x 位于 i,下标从 0 开始的话,x*y 的结果落在 ansArr 的
* “个位”位置 p2 = i + j + 1,“进位”位置 p1 = i + j
* ansArr[p2] 可能之前已累加过其他对齐到 p2 的乘积,所以要先加上
*/
res = ansArr[i + j + 1] + x * y;
// 把“和”的个位写回 p2(当前位置),把“和”的十位以上加到 p1(前一位,作为进位累加)
ansArr[i + j + 1] = res % 10; // 处理相乘的“个位”
ansArr[i + j] += res / 10; // 进位累加到前一位
}
}
// 去掉可能的前导 0(最高位为 0 时跳过它)
int tmp = ansArr[0] == 0 ? 1 : 0;
// 把整型数组转成字符串(此处先 push 数字,再统一加 '0' 转为字符)
string ansString;
while(tmp < sizeNum1 + sizeNum2){
ansString.push_back(ansArr[tmp++]);
}
// 把每个数字 + '0' 变成对应字符
for(auto& c : ansString){
c += '0';
}
return ansString;
}
};
4. 字符串中的第一个唯一字符
思路一
只有26个小写字母,那么就可以两遍线性扫描:
- 第一遍:记录每个字母出现的次数
- 第二遍:找第一个只出现一次的字母并返回索引
代码实现:
class Solution {
public:
int firstUniqChar(string s) {
array<int,26> cnt = {0};
// 遍历整个字符串,把每个字符出现次数 +1。
for(char c : s){
cnt[c - 'a']++;
}
// 从左到右再次遍历,遇到第一个出现次数为 1 的位置,直接返回其下标
for (int i = 0; i < s.size(); ++i) {
if (cnt[s[i] - 'a'] == 1) {
return i;
}
}
// 否则 返回-1
return -1;
}
};
思路二
用队列控制,一遍线性扫描即可,一边遍历一边:
1)更新该字符的计数;
2)把当前下标入队;
3)不断弹出队首中计数>1的下标,
保证队首始终是当前最左且仍唯一的候选。
遍历结束后,队首即答案(队空则 -1)
代码实现:
class Solution {
public:
int firstUniqChar(string s) {
array<int,26> cnt = {0};
queue<int> q;
for(int i = 0; i < s.size(); i++){
// 记录每个字母出现次数
cnt[s[i] - 'a']++;
// 当前索引入队列
q.push(i);
// 队列不为空才能出队
// 不断弹出队首,直到:
// 1) 队列空了(说明当前没有唯一字符),或者
// 2) 队首对应字符的计数 == 1(它就是当前最靠左仍唯一的)
while(!q.empty() && cnt[ s[q.front()] - 'a'] > 1){
q.pop();
}
}
// 循环体结束时:
// 如果 q 非空,q.front() 就是到目前为止最左的唯一字符下标
// 如果 q 为空,说明目前没有唯一字符
return q.empty() ? -1 : q.front();
}
};
5. 验证回文串
验证回文串
思路:
双指针,设 left=0, right=n-1,跳过两端非字母数字字符。将两端字符统一大小写(或统一映射)后比较;若不等返回 false,相等则 left++, right-- 继续,循环结束返回 true。
代码实现:
class Solution {
public:
// 判断是否为字母或数字
static inline bool isAlnum(char c) {
return (c >= '0' && c <= '9') ||
(c >= 'A' && c <= 'Z') ||
(c >= 'a' && c <= 'z');
}
// A-Z 映射到 a-z
static inline char toLower(char c) {
if (c >= 'A' && c <= 'Z') return c + ('a' - 'A');
return c;
}
bool isPalindrome(string s) {
int left = 0, right = (int)s.size() - 1;
while (left < right) {
// 跳过左侧非字母数字
while (left < right && !isAlnum(s[left])) ++left;
// 跳过右侧非字母数字
while (left < right && !isAlnum(s[right])) --right;
// 统一成小写再比较
char a = toLower(s[left]);
char b = toLower(s[right]);
if (a != b) return false;
++left;
--right;
}
return true;
}
};






























