从堆到TopK：一文吃透核心原理与实战应用

0. 前置知识

0.1. 树的概念

树是一种非线性的数据结构，它由$n(n>=0)$个有限节点组成一个具有层次关系的集合

如图，树是一棵倒挂的树，根朝上，叶朝下

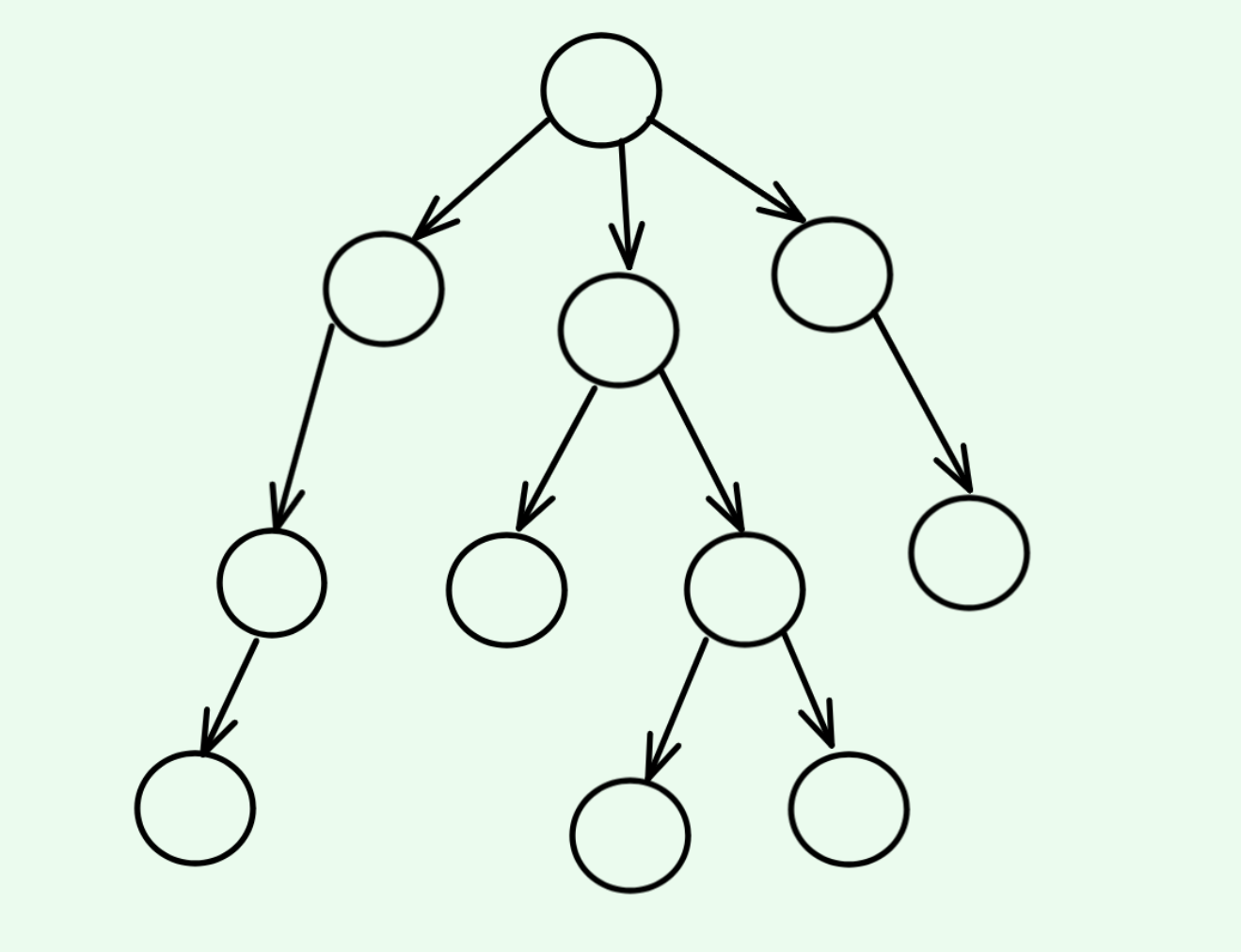
注意：树形结构中，子树之间不能有交集，换句话说，不能成环，否则不是树形结构

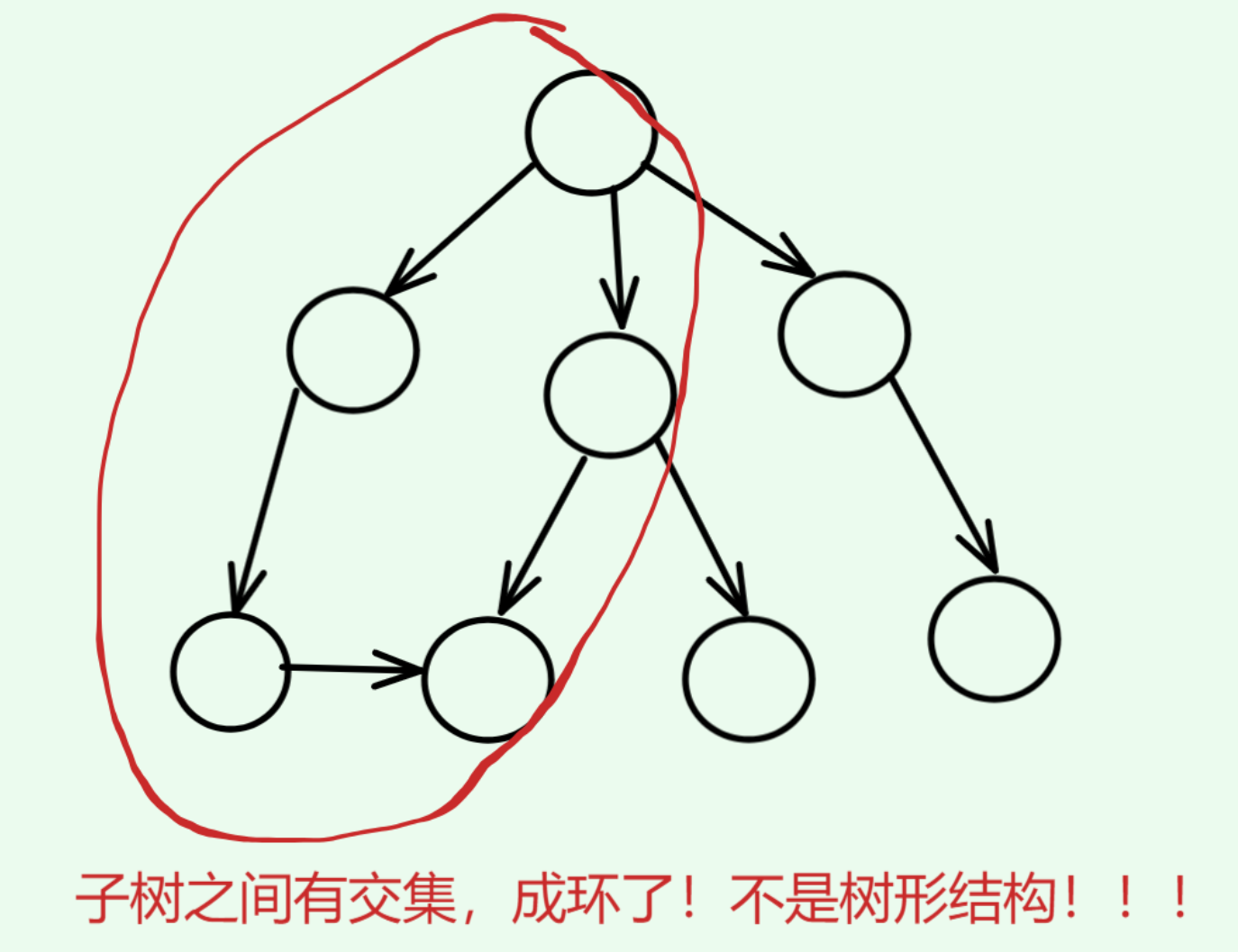
0.2. 树的常见术语

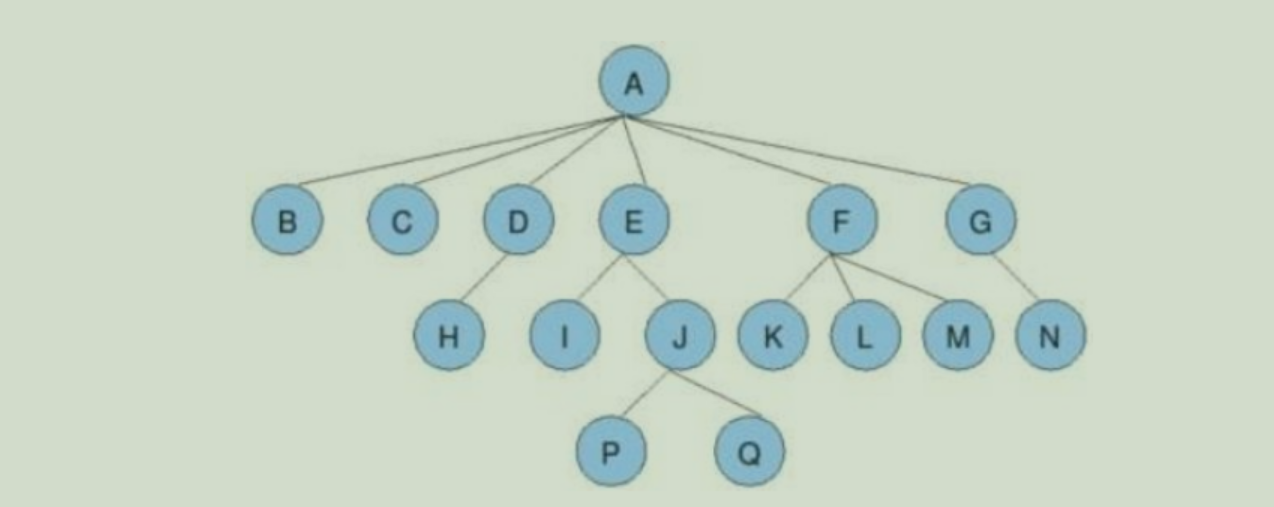
• 节点的度： 一个节点含有的子树的个数，如上图A的为6，E的为2

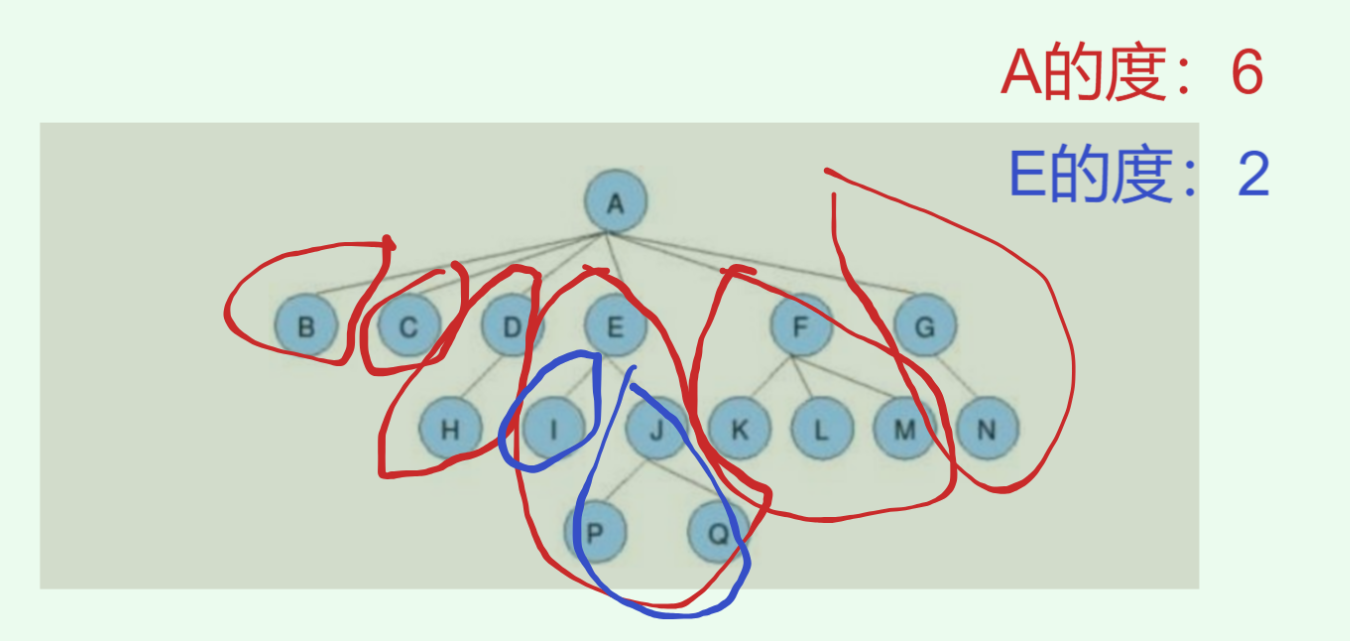
• 叶节点或终端节点： 度为0的节点，即没有孩子的节点，如上图的B C H I P Q K L M N
• 分支节点或非终端节点： 度不为0的节点，即有孩子的节点，如上图的A D E J F G
• 父节点： 有孩子的节点，如B的父节点是A
• 子节点： 如C是A的子节点，P是J的子节点
• 兄弟节点： 有相同父节点的节点互称兄弟节点，如K L M互为兄弟节点
• 树的度： 一棵树中，最大的节点的度是树的度，如上图这棵树，它的度为6
• 边： 连接两个节点的线段，即结点指针
• 节点的层次： 根节点为1，往下依次递增
• 树的高度或深度： 树中节点的最大层次
• 森林： 由$m(m>0)$棵不相交的树构成的集合

0.3. 二叉树

0.3.1. 概念

一棵二叉树是节点的一个有限集合，该集合满足两种情况（或的关系）：

• 可以为空
• 可以由一个根节点加上两棵分别称为左子树和右子树组成

如图：

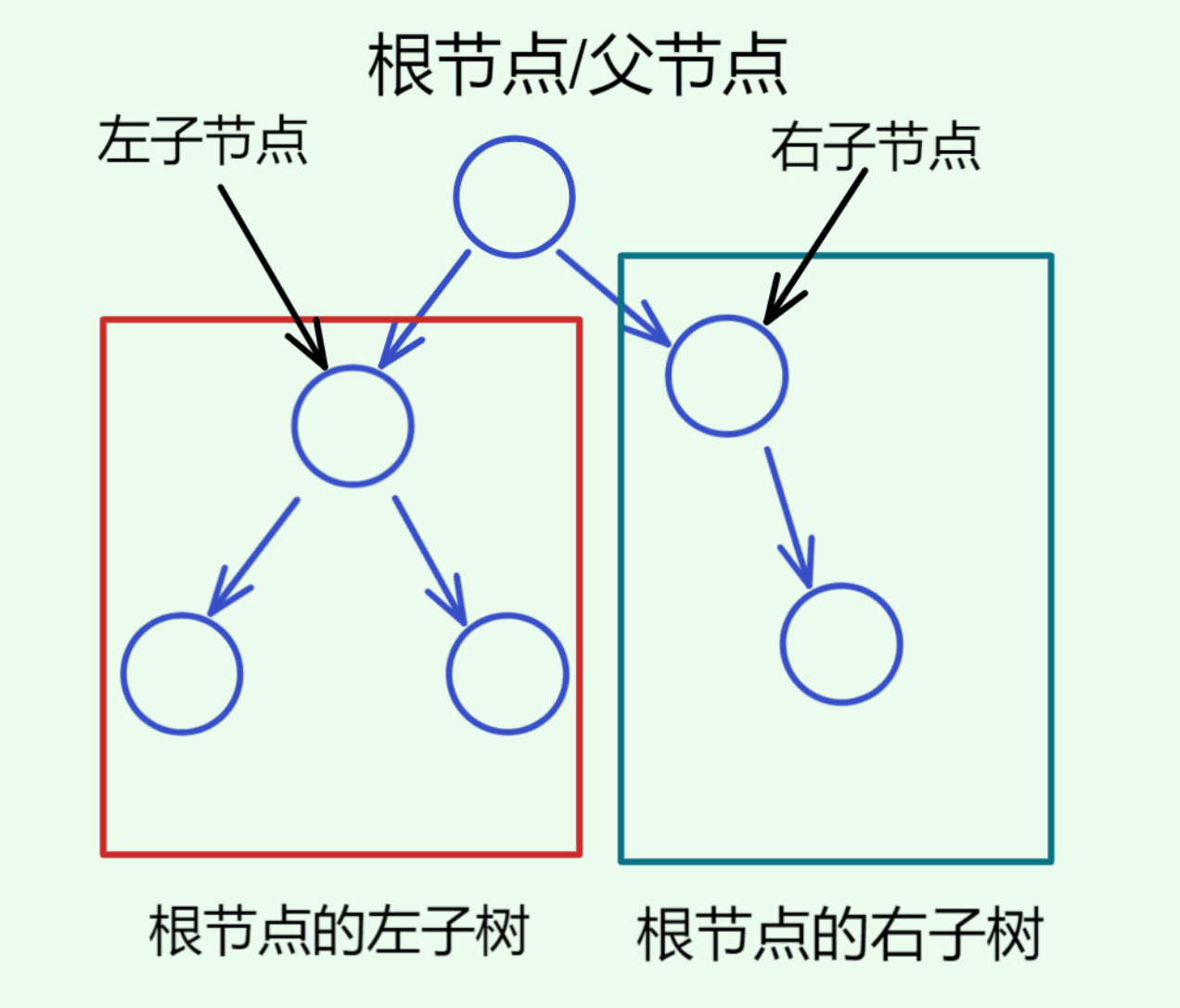
从上图可以看出：

• 二叉树不存在度大于2的节点
• 二叉树有左右之分，次序不能颠倒，所以二叉树是有序树

注意：任意的二叉树都是由以下情况复合而成的：

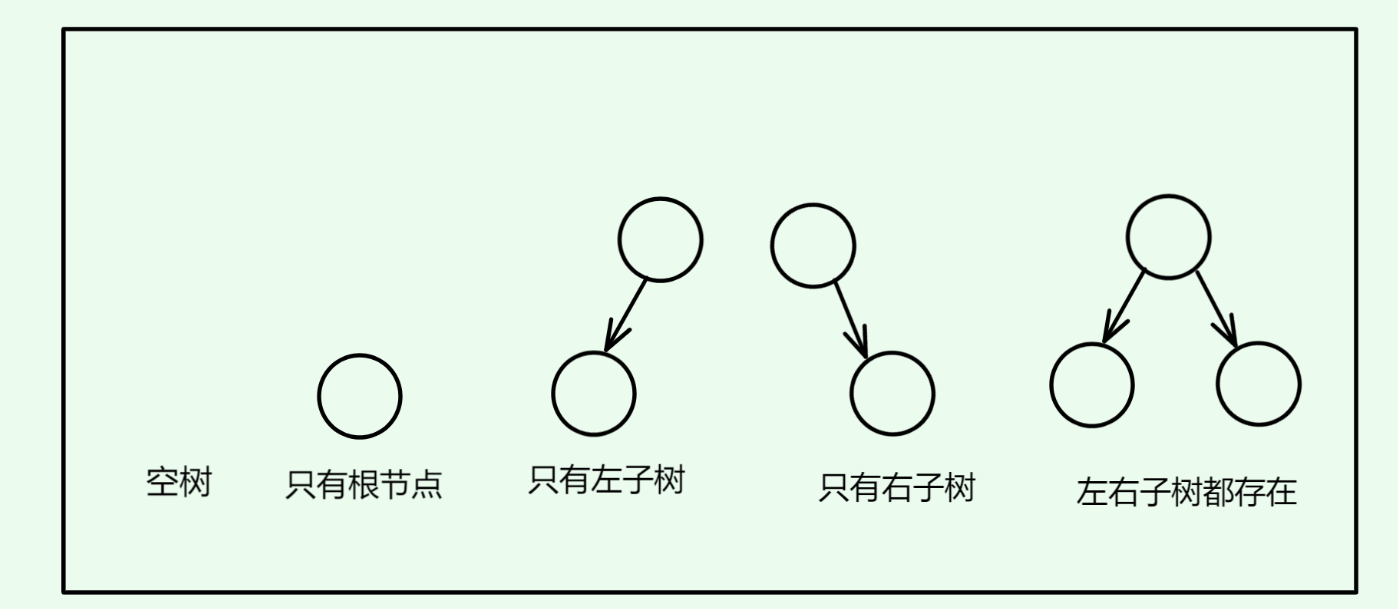
0.3.2. 特殊的二叉树

• 满二叉树： 一个二叉树每层的节点都达到最大值，叶节点的度为0，其余所有节点度为2，例如：一个二叉树的层次为$k$，节点总数是$2^k-1$，这棵树为满二叉树

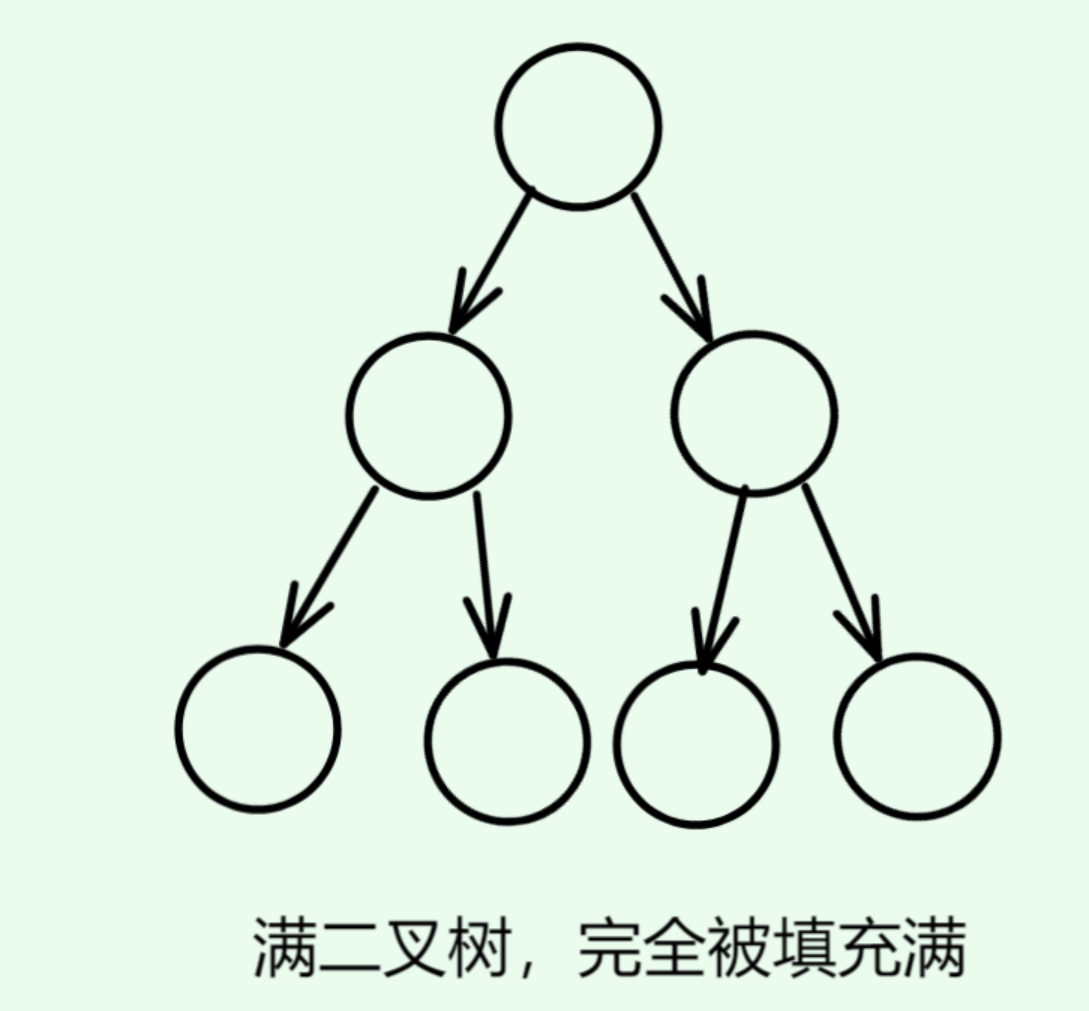
• 完全二叉树： 只有最底层的节点未被填满，且最底层的节点从左到右填充，没有跳跃的二叉树

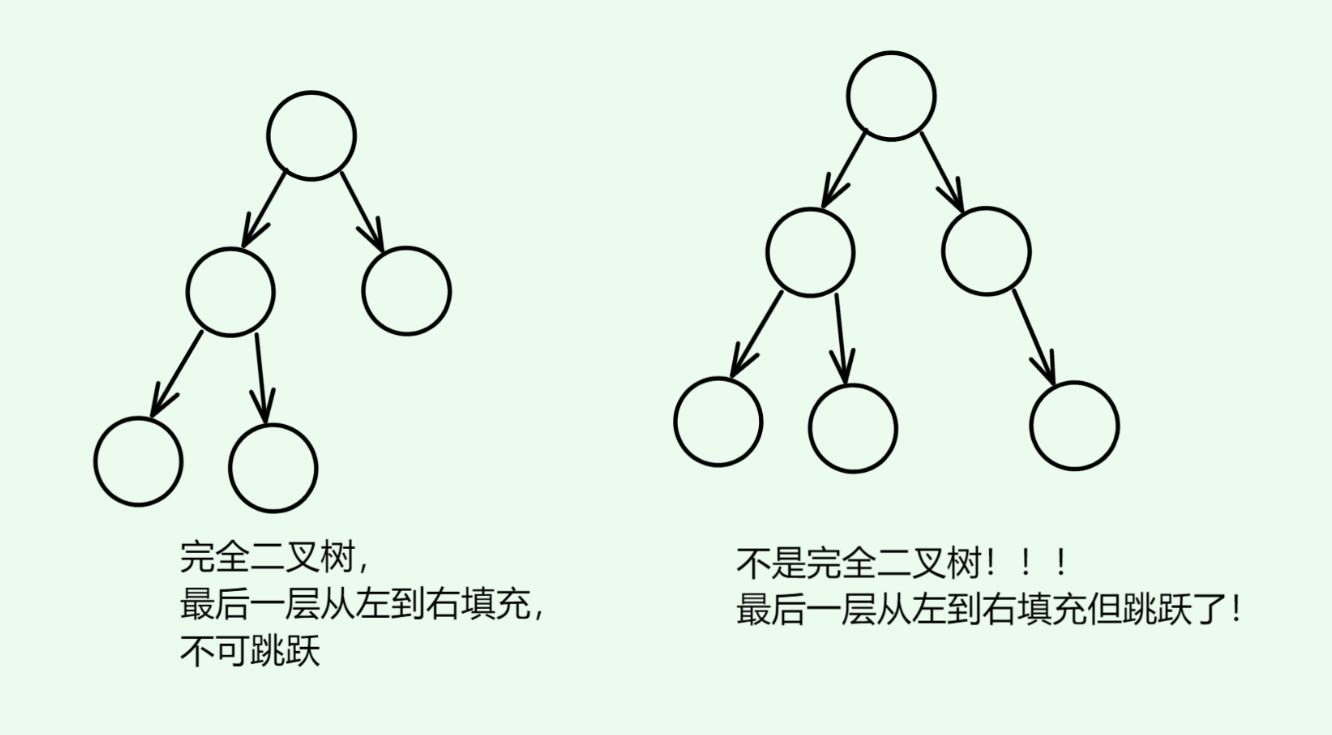
1. 堆的底层原理

堆(heap)是一种满足特定条件的完全二叉树，主要分为两种类型：

• 小顶堆（min heap）：任意节点的值<=其子节点的值
• 大顶堆（max heap）：任意节点的值>=其子节点的值

如图：

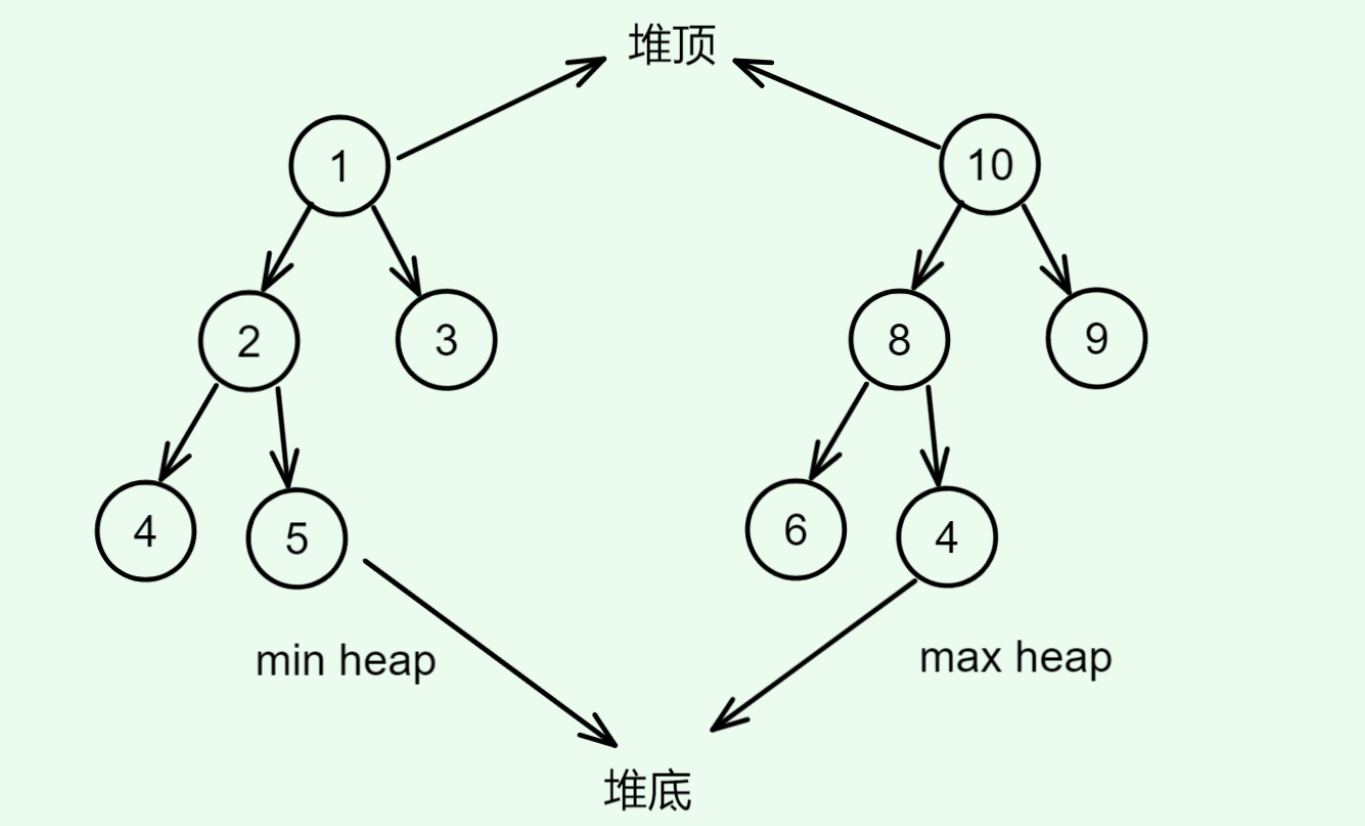
我们将二叉树的根节点称为“堆顶”，将底层最靠右的节点称为“堆底”

1.1. 堆的两个核心定义

1. **逻辑上是完全二叉树：**除了最后一层，每一层的节点数都满，最后一层节点从左到右连续（这样才能用数组紧凑存储，不浪费空间）。
2. **物理上用动态数组存储：**利用完全二叉树的索引规律，不用指针就能找到父节点和子节点，具体关系如下：

• 若父节点的索引为i，左子节点索引为2*i+1，右子节点索引为2*i+2
• 若子节点索引为j，则父节点索引为(j-1)/2（整数除法，会自动取整）
  

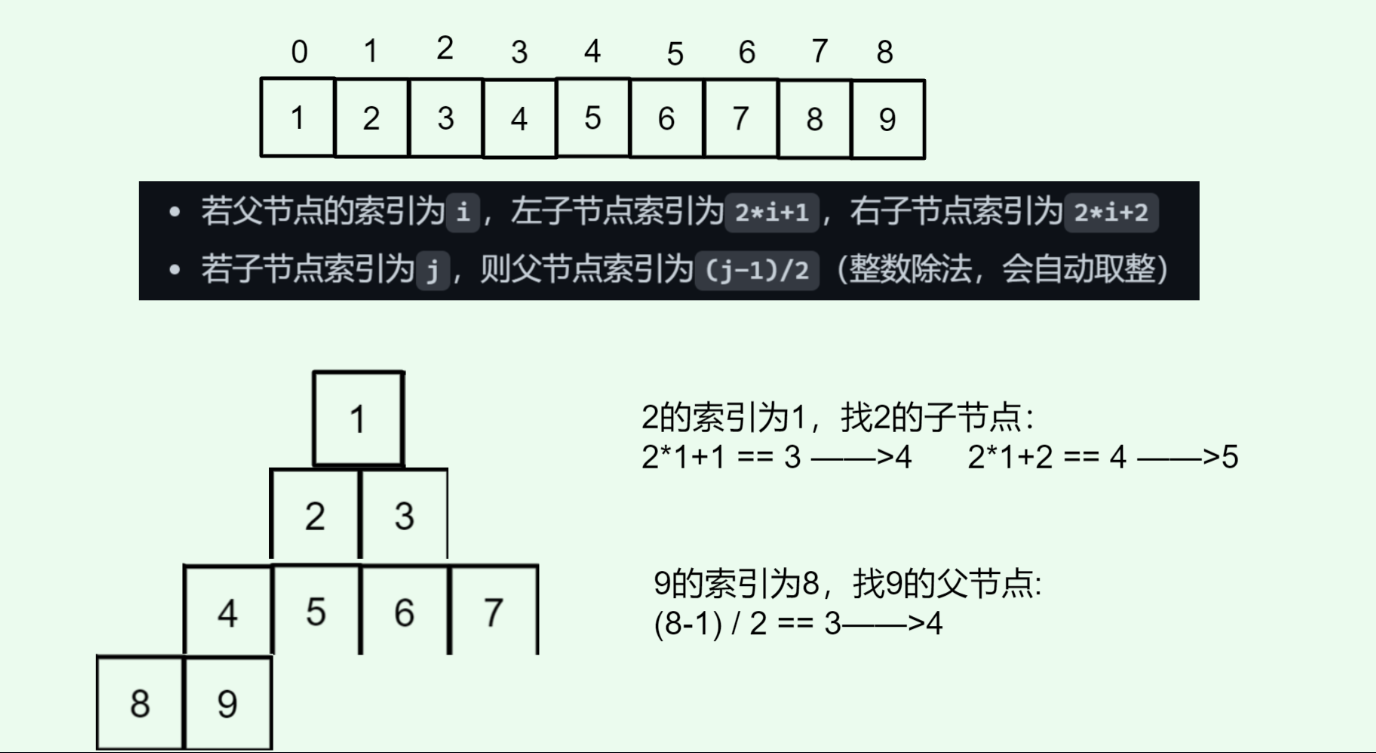
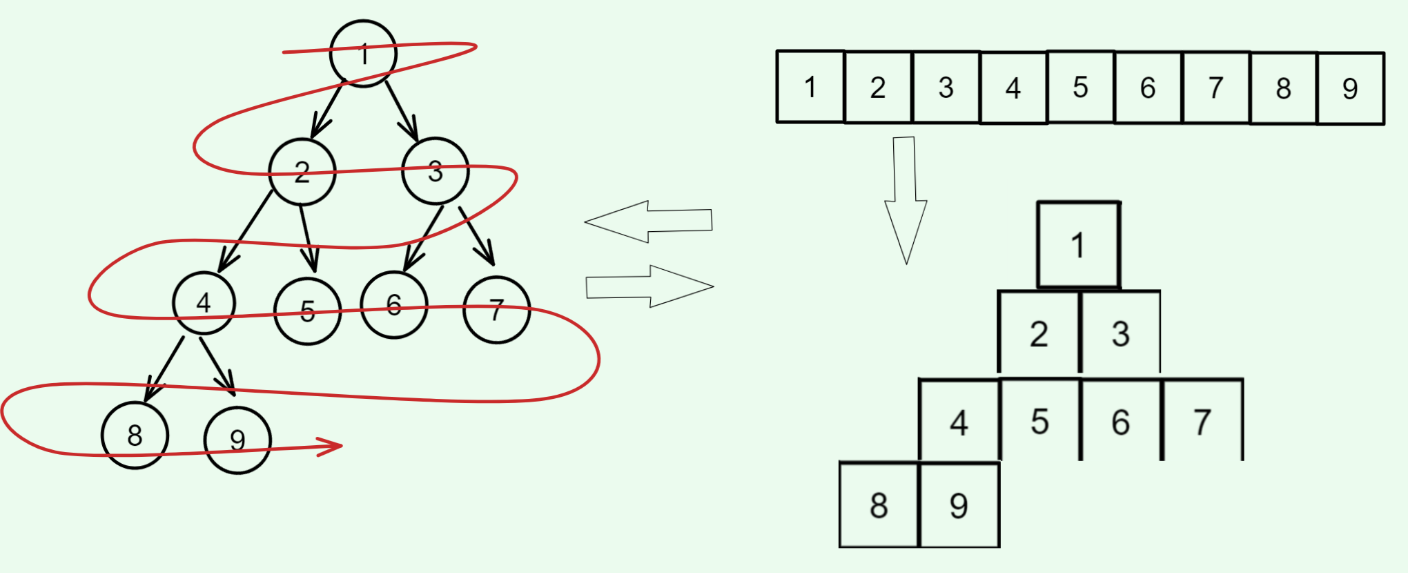
如何将逻辑结构抽象成物理结构（逐层放数据），如何将物理结构转换成逻辑结构（想象细胞分裂），如图：

1.2. 堆的三个核心操作

堆的所有接口（插入、删除堆顶）都依赖向上调整和向下调整，这两个操作能保证堆的结构不被破坏，始终满足两种堆类型的严格规则

(1) 向上调整（push时使用）

场景： 插入元素时，先把元素放到数组末尾（完全二叉树的最有一个叶节点），再通过向上调整把该元素移到正确位置，保证堆的性质。

步骤（以大根堆为例）：

1. 设插入的新元素索引为child，父节点的索引为(child-1)/2
2. 比较_arr[child]和_arr[parent]：若子>父，交换二者
3. 更新child = parent和parent = (child - 1) / 2，重复步骤2，直到child == 0（到根节点）或子 <= 父

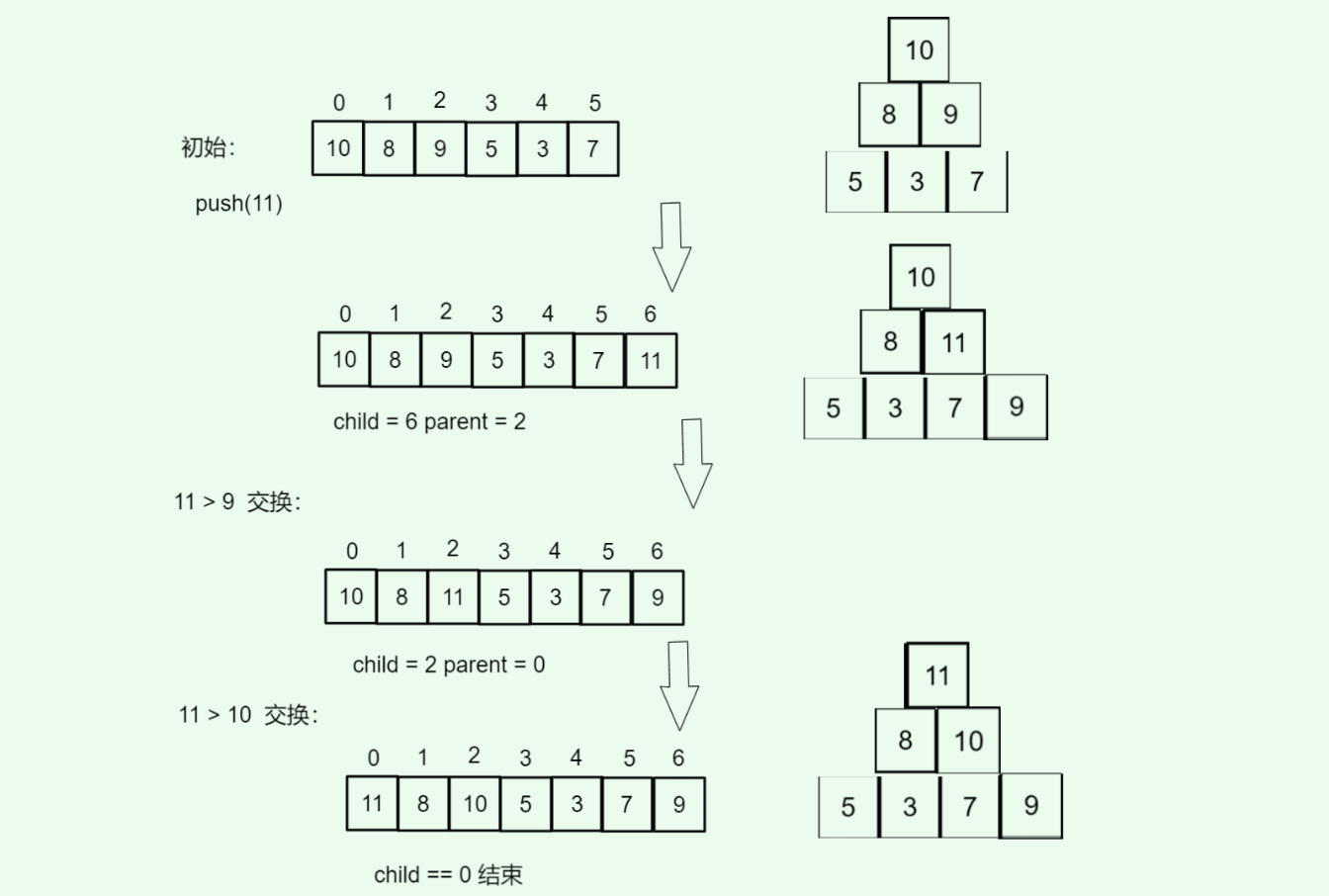
**例子：**往堆[10,8,9,5,3,7]插入11

• 先放入末尾：数组变为[10,8,9,5,3,7,11]

child = 6 , parent = (child - 1) / 2 == 5 / 2 == 2(值9)

• 11 > 9，交换：数组变为[10,8,11,5,3,7,9]

child = 2, parent = (2 - 1) / 2 = 0(值10)

• 11 > 10，交换：数组变为[11,8,10,5,3,7,9]

child == 0，调整结束

图示：

代码实现：

// 向上调整算法
void AdjustUp(size_t child_idx) {
	// 循环判断 维持堆的结构
	while (child_idx > 0) {
		// 找父节点索引
		size_t parent_idx = (child_idx - 1) / 2;

		if (_comp(_arr[parent_idx], _arr[child_idx])) {
			std::swap(_arr[parent_idx], _arr[child_idx]);
			child_idx = parent_idx;
		}
		else {
			break;
		}
	}
}

(2) 向下调整（pop时使用）

场景： 删除堆顶元素(0)时，先把堆顶和最后一个元素(_size - 1)交换，再删除最后一个元素(--_size),最后通过向下调整把新堆顶移到正确位置。

步骤（以大根堆为例）：

1. 设当前节点索引parent，左子节点索引left = 2*parent + 1 ，右子节点索引right = 2*parent + 2
2. 找parent、left、right中最大的值，记为max_idx（注意：若子节点索引>=_size，说明没有这个子节点）
3. 若max_idx != parent(最大值不是父节点)，交换_arr[parent]和_arr[max_idx]
4. 更新parent = max_idx，重复步骤2-3，直到left >= _size（无左子节点，到了叶节点）

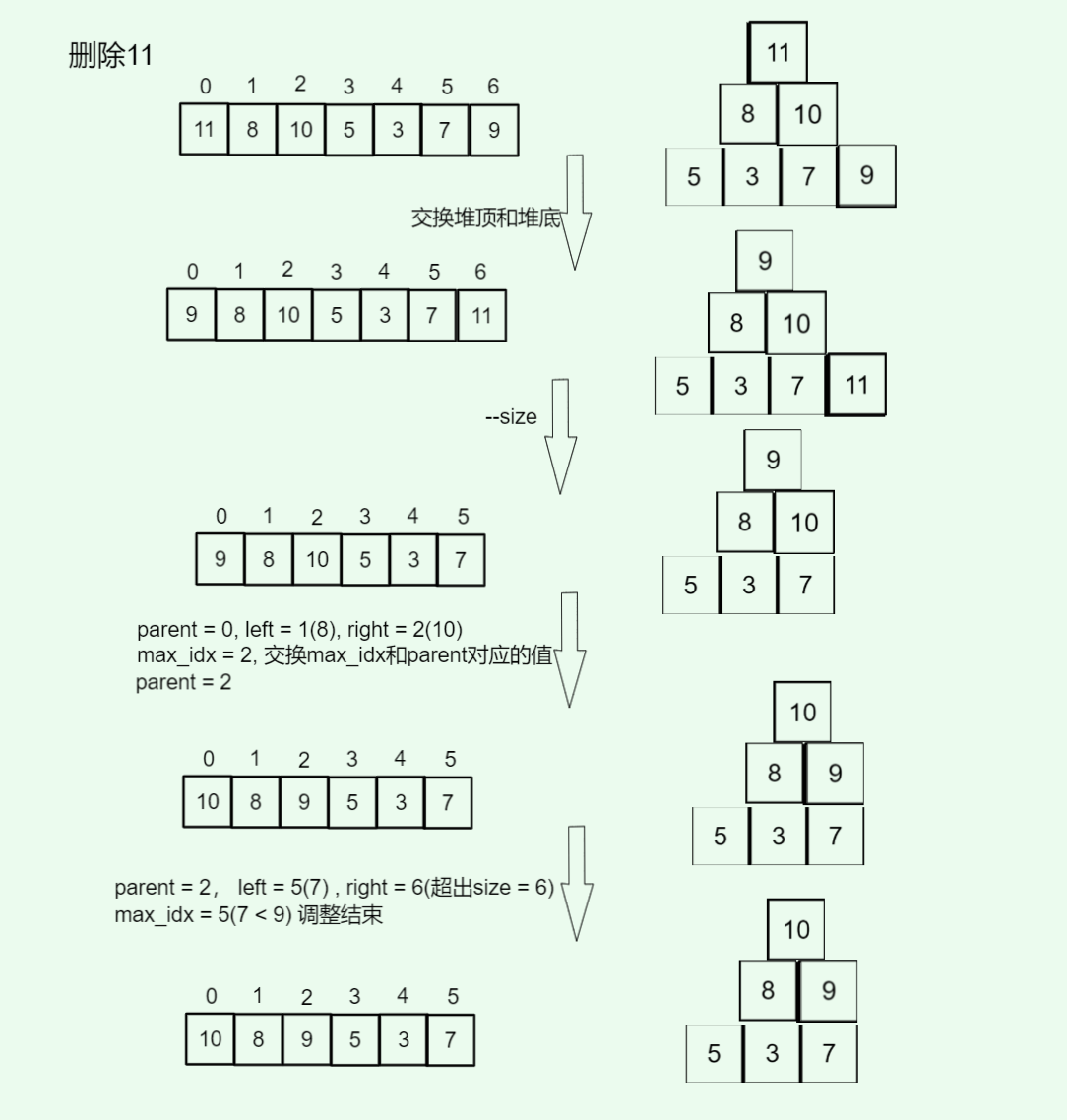
例子： 删除堆顶11[11,8,10,5,3,7,9]：

• 交换堆顶和堆底：数组变为[9,8,10,5,3,7,11],--_size后变为[9,8,10,5,3,7],parent = 0
• left = 1(值8)，right = 2(值10)，max_idx = 2，交换：数组变为[10,8,9,5,3,7],parent = 2
• left = 5 (值7)，right = 6(超出 _size = 6)，max_idx = 5，调整结束

图示：

代码实现：

// 向下调整算法
void AdjustDown(size_t parent) {
	// 假设左孩子是最大的值 先找到左孩子索引
	size_t max_idx = 2 * parent + 1;

	// 循环判断 维持堆的正确结构
	while (max_idx < _size) {
		// 验证假设是否成立
		if (max_idx + 1 < _size && _comp(_arr[max_idx], _arr[max_idx + 1])) {
			++max_idx;// 更新索引 右孩子才是更大的值
		}

		// 现在已经找出两个孩子中最大的一个了 和父节点比较
		if (_comp(_arr[parent], _arr[max_idx])) {
			// 交换二者位置
			std::swap(_arr[max_idx], _arr[parent]);
			// 更新索引
			parent = max_idx; // 父节点索引下移到孩子节点
			max_idx = parent * 2 + 1; // 还是先假设左孩子的值更大
		}
		else {
			break;
		}
	}
}

对于逻辑结构图和物理结构图，我们很容易找到两个孩子中值大的那个，但是计算机不知道怎么寻找，所以我们先假设左孩子的值更大，然后验证，选择出两个孩子中值大的那个

(3) 建堆操作

在某些情况下，我们希望使用一个列表的所有元素来构建一个堆，这个过程被称为“建堆操作”

1. 思路一:借助push实现

我们首先创建一个空堆，然后遍历列表，依次对每个元素执行“入堆操作”，即先将元素添加至堆的尾部，再对该元素执行“从底至顶”堆化。每当一个元素入堆，堆的长度就加一。由于节点是从顶到底依次被添加进二叉树的，因此堆的生长顺序是“自上而下”构建的。设元素数量为$n$，每个元素的入堆操作使用$O(logn)$时间，因此该建堆方法的时间复杂度为$O(nlogn)$

2. 思路二：通过遍历列表堆化实现

• 将列表所有元素原封不动添加到堆中，此时堆的性质没有得到满足
• 倒序遍历堆，依次对每个非叶子节点执行从顶至底堆化即向下调整

每当调整一个节点后，以该节点为根节点的子树就形成一个合法的子堆。而由于是倒序遍历，所以堆的生长顺序是“自下而上”构建的

选择倒序遍历，是能够保证当前节点之下的子树已经是合法的子堆，这样堆化前节点才是有效的

由于叶子节点没有子节点，因此天然就是合法的子堆，无需堆化，最后一个非叶子节点是最后一个节点的父节点，我们从它开始倒序遍历执行堆化：

将无序数组 [3, 1, 4, 1, 5, 9, 2, 6] 转化为大根堆：

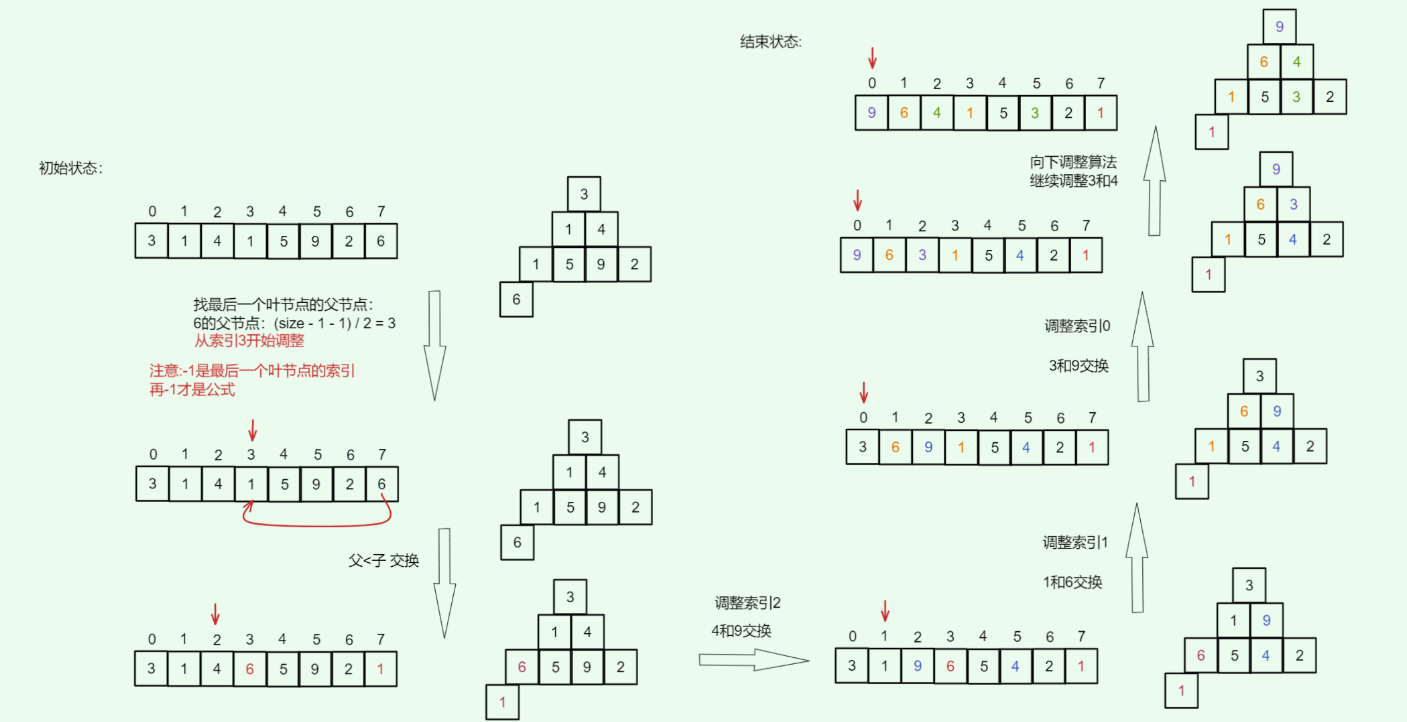
代码实现：

// 构造函数：通过数组初始化堆（核心建堆操作）
max_heap(const std::vector<T>& arr) {
	_arr = arr;
	_size = arr.size();
	if (_size <= 1) return;  // 空堆或单个元素无需调整

	// 从最后一个非叶子节点开始，向前依次调整每个节点
	// 最后一个非叶子节点 = (最后一个节点索引 - 1) / 2
	for (int i = (_size - 2) / 2; i >= 0; --i) {
		AdjustDown(i);  // 对每个非叶子节点执行向下调整
	}
}

2. 堆的核心接口实现

有着前面数组链表的经验，我们很容易实现一个大顶堆，包含插入、删除堆顶、取堆顶、建堆等核心接口，并且支持扩容

#include <iostream>
#include <cassert>
#include <vector>
#include <functional>

namespace Vect {
	template <class T,class Compare = std::less<T>>
	class heap {
	private:
		std::vector<T> _arr; // 底层是动态数组
		size_t _size; // 有效数据个数
		size_t _capacity; // 容量
		Compare _comp; // 决定大顶堆还是小顶堆


		// 向上调整算法
		void AdjustUp(size_t child_idx) {
			// 循环判断 维持堆的结构
			while (child_idx > 0) {
				// 找父节点索引
				size_t parent_idx = (child_idx - 1) / 2;

				if (_comp(_arr[parent_idx], _arr[child_idx])) {
					std::swap(_arr[parent_idx], _arr[child_idx]);
					child_idx = parent_idx;
				}
				else {
					break;
				}
			}
		}


		// 向下调整算法
		void AdjustDown(size_t parent) {
			// 假设左孩子是最大的值 先找到左孩子索引
			size_t max_idx = 2 * parent + 1;

			// 循环判断 维持堆的正确结构
			while (max_idx < _size) {
				// 验证假设是否成立
				if (max_idx + 1 < _size && _comp(_arr[max_idx], _arr[max_idx + 1])) {
					++max_idx;// 更新索引 右孩子才是更大的值
				}

				// 现在已经找出两个孩子中最大的一个了 和父节点比较
				if (_comp(_arr[parent], _arr[max_idx])) {
					// 交换二者位置
					std::swap(_arr[max_idx], _arr[parent]);
					// 更新索引
					parent = max_idx; // 父节点索引下移到孩子节点
					max_idx = parent * 2 + 1; // 还是先假设左孩子的值更大
				}
				else {
					break;
				}
			}
		}

		// 扩容
		void resize() {
			if (_size >= _capacity) {
				size_t new_cap = _capacity == 0 ? 4 : 2 * _capacity;
				_arr.resize(new_cap); // 直接调用vector的扩容接口 不用自己手动实现
				_capacity = new_cap;
			}
		}
	public:
		// 默认构造
		heap():_size(0),_capacity(0){}

		// 构造函数：通过数组初始化堆（核心建堆操作）
		heap(const std::vector<T>& arr) {
			_arr = arr;
			_size = arr.size();
			if (_size <= 1) return;  // 空堆或单个元素无需调整

			// 从最后一个非叶子节点开始，向前依次调整每个节点
			// 最后一个非叶子节点 = (最后一个节点索引 - 1) / 2
			for (int i = (_size - 2) / 2; i >= 0; --i) {
				AdjustDown(i);  // 对每个非叶子节点执行向下调整
			}
		}

		// 拷贝构造 vector自带深拷贝
		heap(const heap& other)
			:_size(other._size)
			,_capacity(other._capacity)
			,_arr(other._arr)
		{ }

		// 析构 vector自带
		~heap(){ }

		/*==================核心接口=========================*/

		// 插入元素（向上调整）
		void push(const T& val) {
			// 先扩容
			resize();         
			_arr[_size] = val; 

			// 向上调整新元素到正确位置
			AdjustUp(_size);   
			++_size;           
		}

		// 删除堆顶元素（向下调整）
		void pop() {
			// 确保不为空才能pop
			assert(!empty());

			// 交换堆顶和堆底元素 
			std::swap(_arr[0], _arr[_size - 1]);
			// 删除堆底元素
			--_size;

			// 向下调整
			AdjustDown(0);
		}

		// 获取堆顶元素
		const T& top()const { assert(!empty()); return _arr[0]; }

		// 判空
		const bool empty() const { return _size == 0; }

		// 获取元素个数
		const size_t size() const { return _size; }

		// 清空堆
		void clear() { _size = 0; }

		// 打印堆
		void PrintHeap() {
			if (empty()) {
				std::cout << "堆为空" << std::endl;
				return;
			}

			for (size_t i = 0; i < _size; i++)
			{
				std::cout << _arr[i] << " " ;
			}
			std::cout << "\n";
		}	
	};
    
    /*=================== 测试代码 =========================*/

void TestAPI() {
	std::cout << "===== 测试大根堆（int类型） =====" << std::endl;

	// 测试默认构造 + push + top
	heap<int> heap1;
	heap1.push(5);
	heap1.push(3);
	heap1.push(8);
	heap1.push(10);
	heap1.push(7);
	heap1.PrintHeap(); // 输出：堆的元素（数组存储）：10 8 5 3 7 （堆顶：10）

	// 测试pop（删除堆顶）
	heap1.pop();
	heap1.PrintHeap(); // 输出：堆的元素（数组存储）：8 7 5 3 （堆顶：8）

	// 测试string类型堆
	std::cout << "\n===== 测试string类型堆 =====" << std::endl;
	heap<std::string> heap3;
	heap3.push("apple");
	heap3.push("banana");
	heap3.push("cherry");
	heap3.push("date");
	heap3.PrintHeap(); // 输出：堆的元素（数组存储）：date cherry banana apple （堆顶：date）
	heap3.pop();
	std::cout << "Pop后堆顶：" << heap3.top() << std::endl; // 输出：cherry
 }
}

3. 堆相关操作的时间复杂度分析

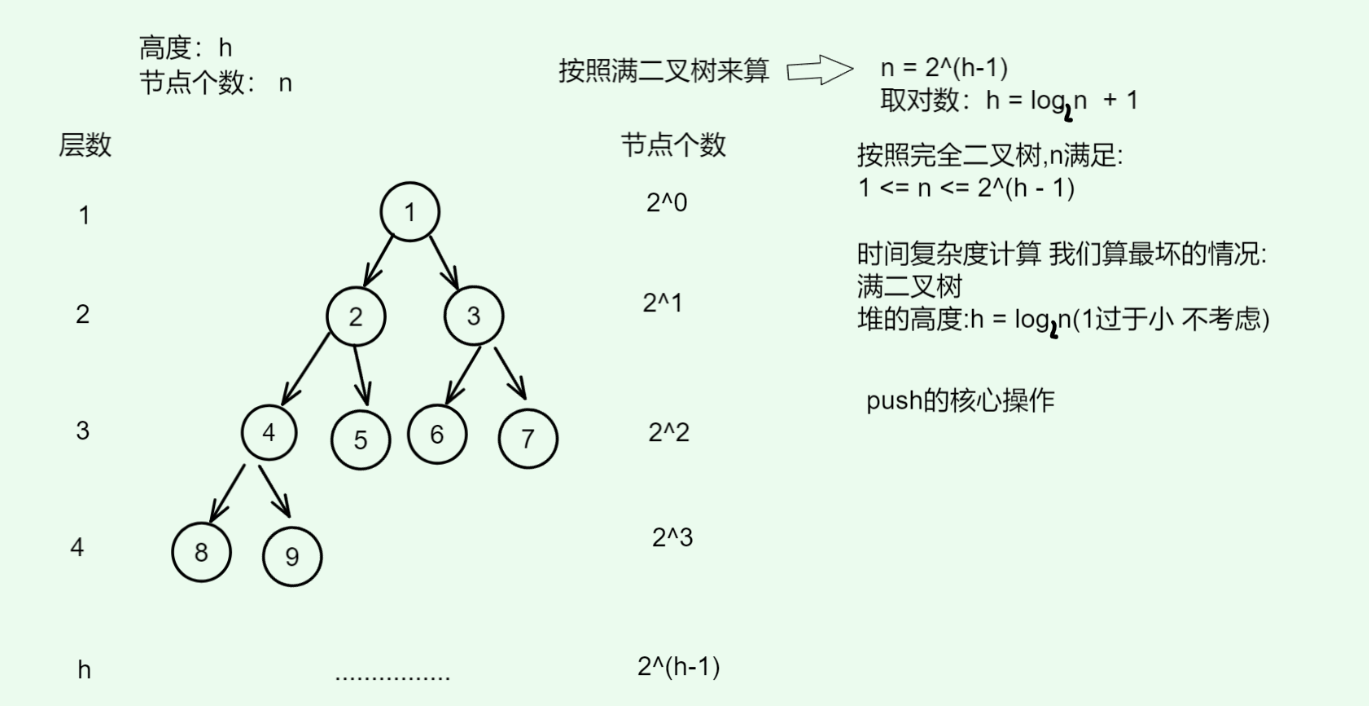
(1) 先明确堆的高度

堆是完全二叉树，设元素个数为$n$，堆的高度是$h$（从根到叶子的层数，根为第一层）满足：$1\le n\le 2^{h-1}$ 而时间复杂度我们考虑的是最坏的情况，即是满二叉树的情况，我们要将堆底元素移到堆顶的情况，此时$n=2^{h-1}$,两边同时取对数得到:$h=lo{g}_{2}n+1$

(2) push(核心向上调整)

向上调整的次数等于新元素从叶子节点到最终位置的路径长度，最长为堆的高度 $h=lo{g}_{2}n+1$，并且满足：

• 每次调整仅涉及一次交换和索引更新$O(1)$；
• 最多执行 $h$ 次调整，因此时间复杂度为 $O(logn)$

(3) pop(核心向下调整)

向下调整的次数等于新堆顶从根节点到最终位置的路径长度，最长为堆的高度 $h=lo{g}_{2}n+1$，并且满足：

• 每次调整涉及 1-2 次比较（找左右子节点最大值）和一次交换$O(1)$；
• 最多执行$h$次调整，因此时间复杂度为 $O(logn)$。

(4) 建堆操作

1. 错误计算!!!

• 假设满二叉树的节点数量为$n$,叶节点的数量为$(n+1)/2$,需要堆化的节点数量为$(n-1)/2$
• 从堆顶到堆底堆化的过程中,每个节点最多对话到叶节点,因此最大迭代次数是二叉树的高度$logn+1$
• 将上述两者相乘,这是一种错误的计算方式,我们没有考略到二叉树底层节点数量远多于顶层节点的特点

2. 正确计算方式

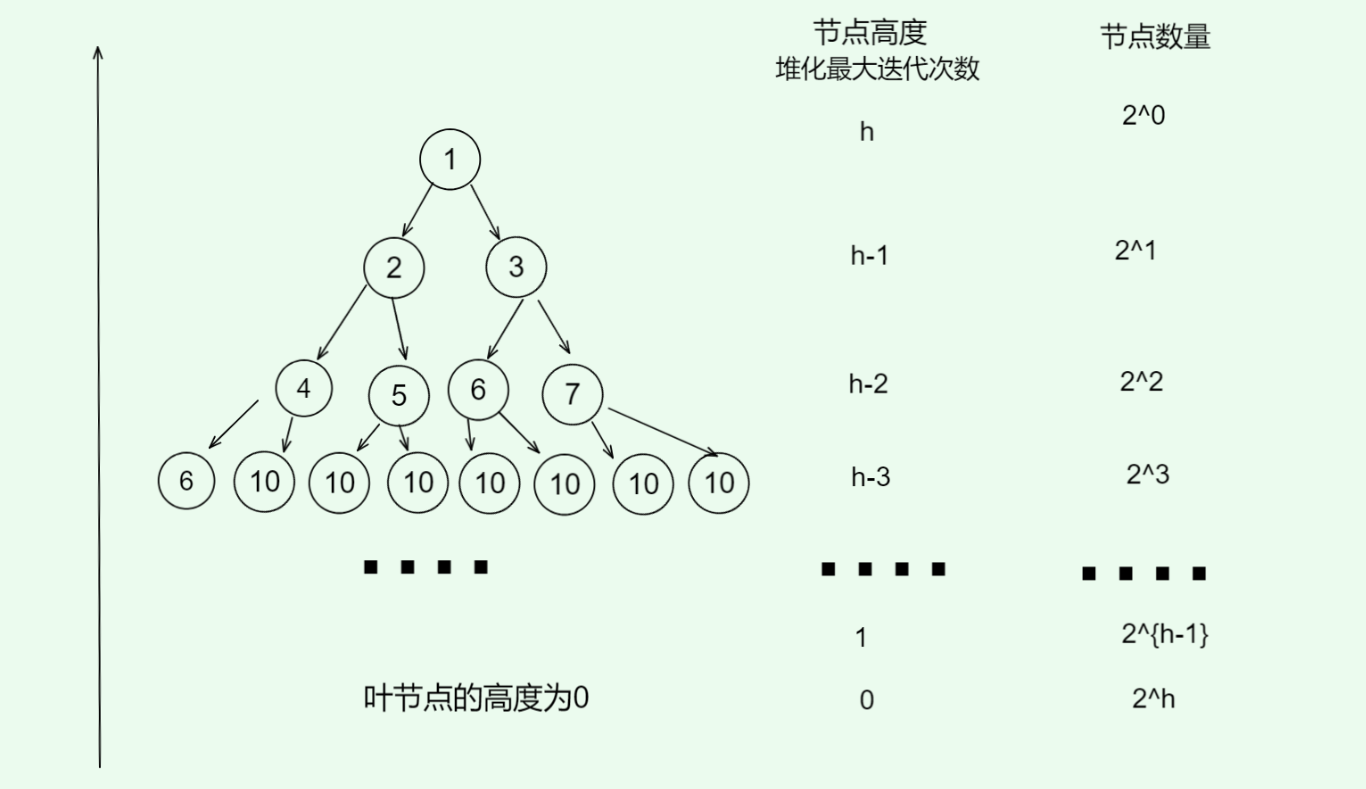
节点从堆顶到堆底的最大迭代次数等于该节点到叶节点的距离,这个距离正是节点高度,所以我们可以对各层的$节点数量\times 节点高度$ 求和,得到所有节点的堆化迭代次数总和

$T(h)=2^{0}h+2^1(h-1)+2^2(h-2)+...+2^{h-1}\times 1$

将$T(h)$乘以2,得到:

$T(h)=2^{0}h+2^1(h-1)+2^2(h-2)+...+2^{h-1}\times 1$

$2T(h)=2^{1}h+2^2(h-1)+2^3(h-2)+...+2^h\times 1$

下式减去上式得到:

$T(h)=-2^{0}h+2^1+2^2+...+2^{h-1}+2^h$

利用等比数列求和公式可以得到:

$T(h)=2^{h+1}-h-2=O(2^h)$

高度为h的满二叉树节点数量$n=2^h-1$,所以时间复杂度为:$ O(2^h)=O(n)$

4. TopK问题

TopK 问题是指从海量数据中高效找出前 K 个最大（或最小）的元素。其核心挑战是在数据量大（甚至无法全部加载到内存） 或 效率要求高的场景下，避免全量排序的高成本，用更优的时间和空间复杂度解决问题。

4.1. 为什么用堆解决？

TopK 问题的关键是 “筛选” 而非 “全量排序”。全量排序（如快排）的时间复杂度是$O(nlogn)$，但当n极大（如 10 亿）时，不仅耗时，还可能因内存不足无法执行。而堆的特性（高效维护最值）能完美适配这一场景，核心原理如下：

1. 找前K大元素：用小顶堆

• 核心逻辑： 用一个容量为K的小顶堆存储候选的前K大元素，堆顶是这些候选元素中的最小值
• 筛选规则： 遍历所有元素时，若当前元素比堆顶大，说明它比候选最小值更有资格成为前K大元素，因此替换堆顶并调整堆结构，否则跳过
• 最终结果： 遍历结束后，小顶堆中存储的就是前K大元素（堆顶存放的是前K大中的最小值）

为什么用小顶堆？

小顶堆的堆顶是最小值，意味着：

• 只要元素比堆顶大，就一定比堆中至少一个元素大，有资格进入候选集
• 堆的大小始终保持K，调整成本是$O(logK)$，远低于全量排序的$O(logn)$

2. 找前K小元素：用大顶堆

逻辑与找前 K 大对称：

• 用容量为 K 的大顶堆存储候选元素，堆顶是候选元素中的最大值；
• 遍历元素时，若当前元素比堆顶小，则替换堆顶并调整；
• 最终堆中元素即为前 K 小元素（堆顶是前 K 小中的最大值）。

4.2. 实现思路（以前K大元素为例）

数据：[5,3,8,10,7,1,9,2,6,4]，K=3：

1. 初始化小顶堆： 取前K个元素[5,3,8]，构建小顶堆。建堆后堆顶为3，堆结构：[3,5,8]
2. 遍历剩余元素: 从第K个元素开始,即[10,7,1,9,2,6,4]

• 元素 10：10 > 堆顶 3 → 替换堆顶为 10，调整后堆：[5,10,8]（堆顶 5）；
• 元素 7：7 > 堆顶 5 → 替换堆顶为 7，调整后堆：[7,10,8]（堆顶 7）；
• 元素 1：1 < 堆顶 7 → 跳过；
• 元素 9：9 > 堆顶 7 → 替换堆顶为 9，调整后堆：[8,10,9]（堆顶 8）；
• 元素 2：2 < 堆顶 8 → 跳过；
• 元素 6：6 < 堆顶 8 → 跳过；
• 元素 4：4 < 堆顶 8 → 跳过。

3. 提取结果: 小顶堆中剩余元素[8,10,9]即为前 3 大元素（排序后为[7,8,10]，注意堆的存储顺序不直接是排序结果，需额外处理）。

4.3. 使用场景

TopK 问题在工程中应用广泛，核心场景是 “海量数据 + 筛选最值”：

1. 日志分析：从千万级访问日志中找访问量前 10 的 IP 地址；
2. 电商平台：实时计算销量前 100 的商品、用户消费金额前 50 的客户；
3. 搜索引擎：根据关键词热度排序，返回前 10 的相关结果；
4. 大数据处理：在分布式系统中（如 Hadoop），对分片数据的局部 TopK 再聚合，得到全局 TopK。

这些场景的共性：数据量大（n极大）、K 较小（通常远小于n），需要高效（时间$O(nlogK)$）且低内存（空间$O(K)$）的解决方案。

4.4. 代码实现

// TopK问题

// 找前K大 小顶堆维护
static std::vector<int> TopK_max(const std::vector<int>& data, size_t K) {
	// 边界处理 K=0或者K>=数据量直接返回该数组
	if (K == 0 || K >= data.size()) {
		return data;
	}

	// 小顶堆（greater 父 < 子）
	heap<T, std::greater<T>> minHeap;

	// 遍历数组
	for (size_t i = 0; i < data.size(); i++)
	{
		if (minHeap.size() < K) {
			// 堆中不足K个元素 直接放进去
			minHeap.push(data[i]);
		}
		else if (data[i] > minHeap.top()) {
			// 当前元素比堆顶大
			// 说明堆顶的最小值不够资格进前K 要淘汰
			minHeap.pop(); // 淘汰堆顶
			minHeap.push(data[i]); // 插入新元素
		}
		// 否则 data[i] <= 堆顶 直接丢弃 连第K大都排不上
	}

	// 此时堆中正好保存了无序的前K大元素
	std::vector<T> ret_nums;
	while (!minHeap.empty()) {
		ret_nums.push_back(minHeap.top());
		minHeap.pop();
	}
	return ret_nums;
}


// 找前K小 用大顶堆维护
static std::vector<T> TopK_min(const std::vector<T>& data, size_t K) {
	if (K == 0 || K >= data.size()) return data;

	// 大顶堆（less 父 > 子）
	heap<T, std::less<T>> maxHeap;

	// 遍历数组
	for (size_t i = 0; i < data.size(); i++)
	{
		if(maxHeap.size() < K){
			// 堆中不足K个元素 直接放
			maxHeap.push(data[i]);
		}
		else if (data[i] < maxHeap.top()) {
			// 如果当前元素比堆顶还小
			// 说明堆顶最大值不够资格进前K小 淘汰
			maxHeap.pop(); // 淘汰堆顶
			maxHeap.push(data[i]); // 插入新元素
		}
		// 否则 如果data[i] >= 堆顶 直接丢弃 连第K小都排不上
	}

	// 此时堆中正好保存了无序的前K小元素
	std::vector<T> ret_nums;
	while (!maxHeap.empty()) {
		ret_nums.push_back(maxHeap.top());
		maxHeap.pop();
	}
	return ret_nums;
}

测试代码：

void TestTopK() {
	std::vector<int> nums = { 5, 3, 8, 10, 7, 2, 9 ,100,2058,60,102,5461};

	auto top3max = heap<int>::TopK_max(nums, 3);
	std::cout << "前3大：";
	for (auto e : top3max) std::cout << e << " ";
	std::cout << "\n";

	auto top3min = heap<int>::TopK_min(nums, 3);
	std::cout << "前3小：";
	for (auto e : top3min) std::cout << e << " ";
	std::cout << "\n";
}

5. 总结

到这里，我们其实已经把堆这一块的核心内容拆解得差不多了。从二叉树的铺垫，到堆的定义与调整操作，再到复杂度分析，最后结合 TopK 问题做了实战，其实就是一条“从理论到应用”的学习闭环。

回过头看：

• 堆的底层逻辑：本质上就是一个完全二叉树 + 数组存储的组合，用“父子索引关系”来做快速的上调、下调操作。看似抽象，其实实现起来很简洁。

• 堆的作用场景：你可以把它当成一种“随时能取出最大/最小值”的利器。像优先级队列、调度系统、实时统计 TopK 热点，堆都能派上用场。

• TopK 的思路：记住一句话就行——

  1. 前 K 大 → 用小顶堆守着最小值

  2. 前 K 小 → 用大顶堆守着最大值
     这样堆顶永远是“边界元素”，剩下的就是不停更新、维持堆的有序性。

一点小感悟：数据结构和算法，其实都像是在训练我们“换个角度思考”的能力。堆教会我们的，不只是怎么写一个优先队列，更是如何在“局部”维护“全局最优”。当你能把这种思维迁移到工程里，就会发现很多看似复杂的问题，思路一下就清晰了。