数据结构

图

邻接矩阵

• 定义

  用两个数组来表示图：一个一维数组存储图中顶点信息，一个二维数组（称为邻接矩阵）存储图中边（无向图）或弧（有向图）的信息

• 优点

容易获得每个顶点的度，特别是对于有向图，获得顶点i的度，即arc[i]的值，入度也只需遍历第i列，即arc【】【i】

• 缺点

  对于边数顶点相对较少的图，浪费了极大的存储空间

邻接表

• 定义

  对于顶点数组，每个数据元素需要存储指向第一个邻接点的指针

  每个顶点Vi的所有构成一个线性表，并用单链表存储，无向图成为顶点Vi的边表，有向图成为顶点Vi为弧尾的出边表

  顶点表的各个顶点由data和firstEdge两个域表示，data是数据域，存储顶点的信息，firstEdge是指针域，指向此顶点的第一个邻接点

  边表节点由adjvex和next两个域组成

  adjvex是邻接点域，存储某顶点的邻接点在顶点中的下标，next则存储下一个节点的指针

• 优点

  节省空间，只存储实际存在的边

• 缺点

  如果要求顶点的度，就可能要遍历一个链表

  对于无向图，如果要删除一个边，就需要在两个链表上查找并删除

十字链表

• 定义

  把邻接表和逆邻接表结合起来，就得到了十字链表，所以十字链表也是专门为有向图设计的。

  顶点表节点结构

  firstIn	firstOut	data
  入边表第一个节点	出边表第一个节点	数据

  边表顶点结构

  tailvex	headvex	headlink	taillink
  弧起点（弧尾）	弧终点（弧头）	入边表指针域，终点相同的下一条边	出边表指针域，起点相同的下一条边

• 优点

  可以同时访问出入度

• 缺点

  空间浪费，复杂

邻接多重表

• 定义

  边表节点结构 ，用来存储无向图

  ivex	ilink	jvex	jlink
  顶点在顶点表中的下标	顶点在顶点表中的下标	附顶点 ivex的下一条边	附顶点jvex的下一条边

  • 优点

    可以同时访问出入度

  • 缺点

    空间浪费，复杂

  邻接多重表和邻接表的差别，仅仅在于同一条边在邻接表中用两个结点表示，而在邻接多重表中只有一个结点。
  所以上述的删除（V0,V2）边，只需要把图中浅蓝色的边对应的链接指向改成^即可。

边集数组

• 定义

  begin	end
  边起点下标	边终点下标

  边集数组由两个一维数组组成，

  一个存储顶点的信息，【顶点数组】

  另一个存储边的信息，边数组的每个数据元素由一条边的起点下标和重点下表组成

• 优点

  有向图边操作简单

• 缺点

  统计出入度很难

齐老的顺口溜

邻接矩阵存密图，邻接链表存疏图

十字链表存有向，邻接多重存无向

边集数组很简单，统计出入很困难

最小生成树

定义

​ 一个有 n 个结点的连通图的生成树是原图的极小连通子图，且包含原图中的所有 n 个结点，并且有保持图连通的最少的边。最小生成树可以用kruskal（克鲁斯卡尔）算法或prim（普里姆）算法求出。

​ 在一给定的无向图G = (V, E) 中，(u, v) 代表连接顶点 u 与顶点 v 的边（即），而 w(u, v) 代表此边的权重，若存在 T 为 E 的子集（即）且为无循环图，使得

的 w(T) 最小，则此 T 为 G 的最小生成树。

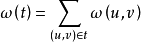
最小生成树其实是最小权重生成树的简称。

Prim算法【加点】

其中顶点集合为V，边集合为E；

重复下列操作，直到Vnew= V

在集合E中选取权值最小的边<u, v>，其中u为集合Vnew中的元素，而v不在Vnew集合当中，并且v∈V（如果存在有多条满足前述条件即具有相同权值的边，则可任意选取其中之一）；

b.将v加入集合Vnew中，将<u, v>边加入集合Enew中；

4).输出：使用集合Vnew和Enew来描述所得到的最小生成树。

Kruskal算法【加边】

假设 WN=(V,{E}) 是一个含有 n 个顶点的连通网，则按照克鲁斯卡尔算法构造最小生成树的过程为：先构造一个只含 n 个顶点，而边集为空的子图，若将该子图中各个顶点看成是各棵树上的根结点，则它是一个含有 n 棵树的一个森林。之后，从网的边集 E 中选取一条权值最小的边，若该条边的两个顶点分属不同的树，则将其加入子图，也就是说，将这两个顶点分别所在的两棵树合成一棵树；反之，若该条边的两个顶点已落在同一棵树上，则不可取，而应该取下一条权值最小的边再试之。依次类推，直至森林中只有一棵树，也即子图中含有 n-1条边为止。