图的常见存储结构及各自的优缺点

以下说法均建立在简单图上，即无环无重复边的图。

本文将介绍图的常见存储结构及各自的优缺点

1. 邻接矩阵
2. 邻接表
3. 十字链表
4. 邻接多重表
5. 边集数组

邻接矩阵

用两个数组来表示图：一个一维数组存储图中顶点信息，一个二维数组（称为邻接矩阵）存储图中边（无向图）或弧（有向图）的信息

若图有n个顶点，则邻接矩阵则为一个n*n的方阵
定义为：

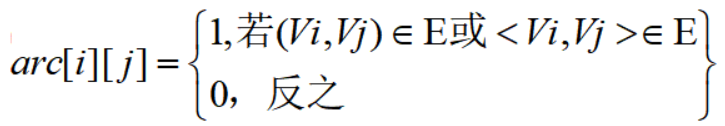
eg:

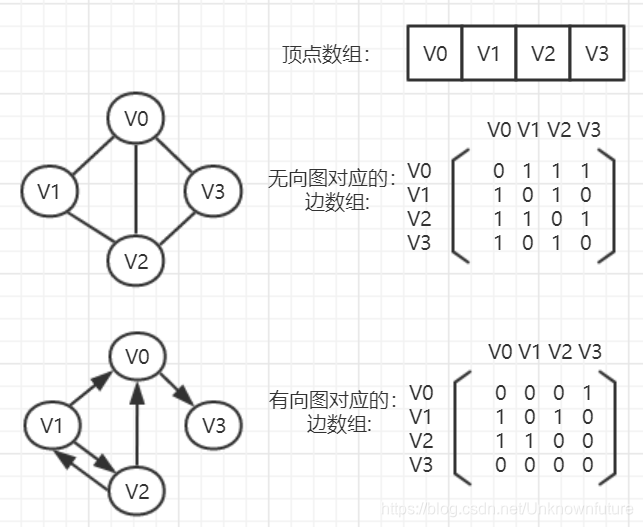
根据定义，可知对角线的值无论是无向图还是有向图均为0。
对于无向图，邻接矩阵是对称的，但有向图并无该特性。

优点：

容易获得每个顶点的度，特别是对于有向图，获得顶点i的出度，只需遍历第i行，即arc[i]的值，入度也只需遍历第i列，即arc[][i]。

缺点：

对于边数相对顶点较少的图，浪费了极大的存储空间。

邻接表

如上所述，顺序存储可能造成存储空间浪费的问题，所以就引出了链式存储结构。

• 对于顶点数组，每个数据元素需要存储指向第一个邻接点的指针。
• 每个顶点Vi的所有邻接点构成一个线性表，并用单链表存储；无向图称为顶点Vi的边表，有向图称为顶点Vi为弧尾的出边表
  
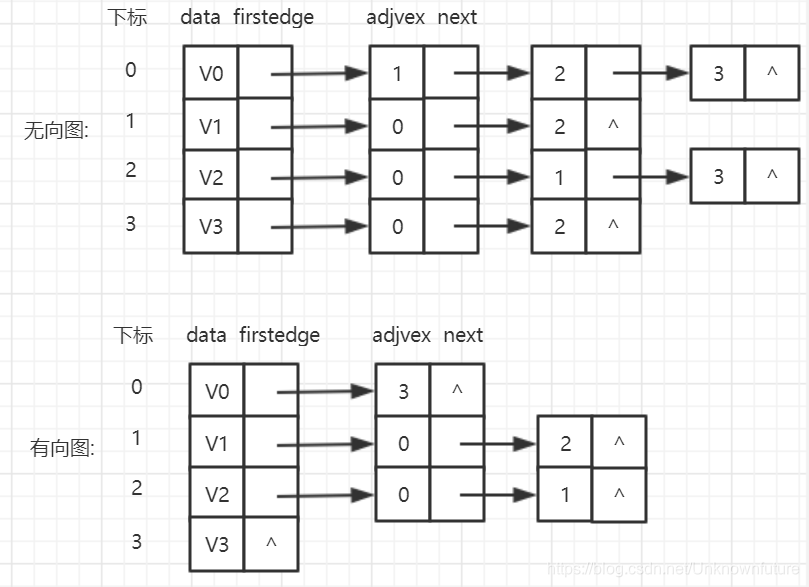
  如图
• 顶点表的各个结点由data跟firstedge两个域表示。
  data是数据域，存储顶点的信息，firstedge是指针域，指向此顶点的第一个邻接点。
• 边表结点由adjvex和next两个域组成。
  adjvex是邻接点域，存储某顶点的邻接点在顶点中的下标，next则存储指向边表中下一个结点的指针。

但正如定义，对于有向图，邻接表只存储了各顶点相应的出边，若要便利地获得入度，则可以同理建立一个逆邻接表：对每个顶点都建立一个链接为Vi为弧头的表

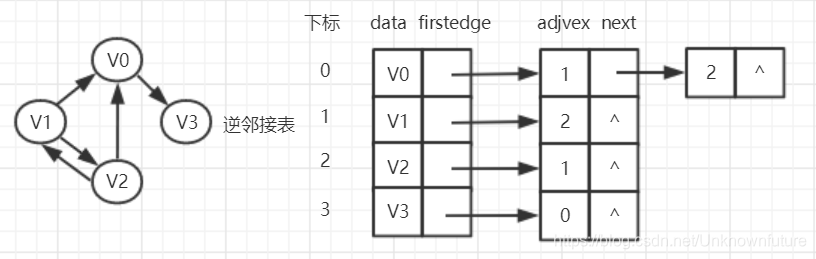
缺点：
对于有向图，出度入度是不兼得的，要两样都获得就只能分别建立、遍历对应的邻接表和逆邻接表。空间利用率和效率也不高。

十字链表

把邻接表和逆邻接表结合起来，就得到了十字链表。所以十字链表也是专门为有向图设计的。

• 重新定义顶点表结点结构为：
  
  firstin、firstout 分别指向入边表、出边表中的第一个结点

• 重新定义边表结点结构为：
  
  注意 tail、head分别指弧尾、弧头，不要混乱。
  tailvex、headvex分别指弧起点（即弧尾）、弧终点（即弧头）在顶点表中的下标。
  headlink是指入边表指针域，指向终点相同的下一条边（即弧头相同，所以命名为headlink）;
  taillink是指出边表指针域，指向起点相同的下一条边（即弧尾相同，所以命名为taillink）

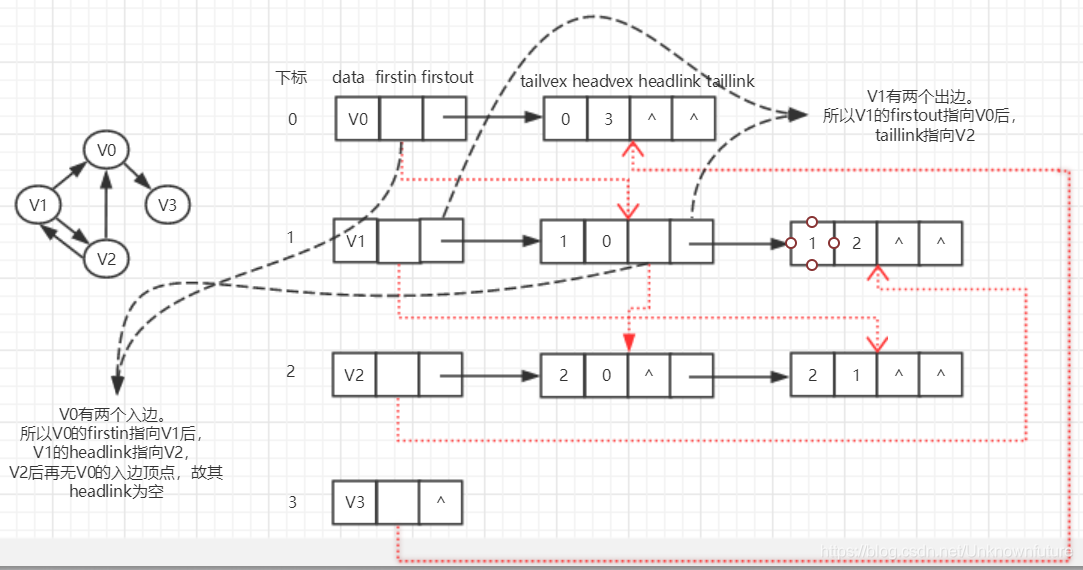
当然了，并不是说十字链表一定比邻接表好，也是看实际需求是否需要同时访问出入度。

邻接多重表

既然十字链表是有向图的优化存储结构，那邻接表对于无向图有没有什么缺点呢？答案是肯定的。

若我们关注的重点是顶点，那邻接表自然是不错的选择；
但如果更关注边的操作，比如删除边（V0,V2）

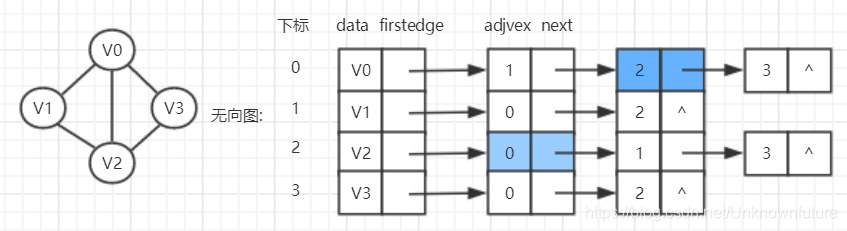
我们就需要删除图中的两个阴影结点，显然是比较麻烦的。

所以邻接多重表就应运而生了。

• 重新定义边表结点结构为：
  
  其中ivex、jvex是与某条边依附的两个顶点在顶点表中的下标，
  ilink指向依附顶点 ivex的下一条边，同理，
  jlink指向依附顶点 jvex的下一条边。

当然，因为是无向图，所以ivex跟jvex是什么顺序都是无所谓的，但为了绘图方便，此处将ivex值设置得与一旁顶点下标相同。

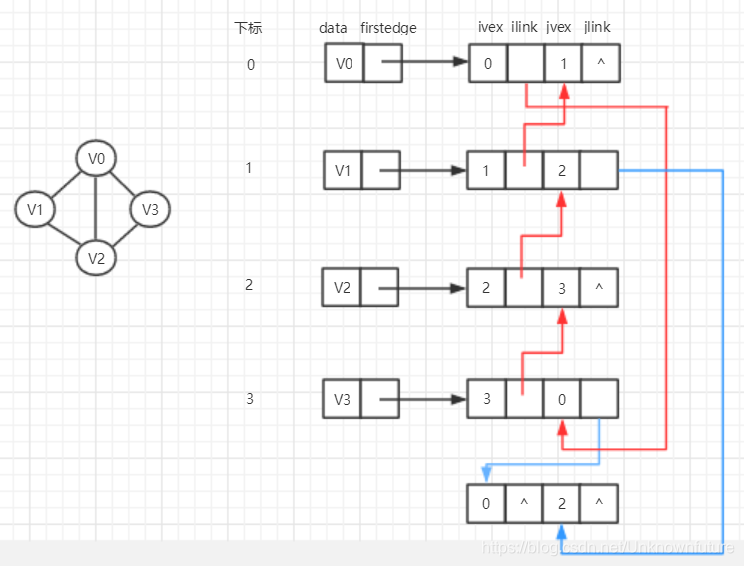
邻接多重表和邻接表的差别，仅仅在于同一条边在邻接表中用两个结点表示，而在邻接多重表中只有一个结点。
所以上述的删除（V0,V2）边，只需要把图中浅蓝色的边对应的链接指向改成^即可。

边集数组

邻接表关注的是顶点，十字链表则是对有向图的优化，但关注的重点仍然是顶点；邻接多重表则是对无向图的优化，关注重点是边。

那缺了什么了？没错，就是有向图的关注边的操作时所用的结构，就是本节所说的边集数组。

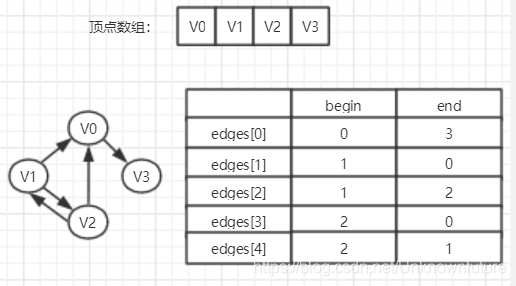
边集数组由两个一维数组构成。
一个存储顶点的信息（即顶点数组），
另一个是存储边的信息：边数组的每个数据元素由一条边的起点下表（begin）、终点下标（end）组成。

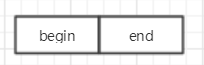
人如其名，边集数组关注的是边的集合。在边集数组中查找一个顶点的度需要扫描整个边数组，效率并不高。因此更适合与边相关的操作，而不适合对顶点相关的操作。

汇总

结构	优点	缺点	关注点
邻接矩阵	通用性强	需求空间大
邻接表	节省空间	对有向图无法兼备出度入度	顶点
十字链表	对有向图兼得出度入度		有向图、顶点
邻接多重表	无向图边操作简单		无向图、边
边集数组	有向图边操作简单		有向图、边

缺点为空并不代表没有缺点，关注点一列的对应的其实就是优点，反之则是缺点。

参考内容：《大话数据结构》
若有误欢迎指出。