博主参加了2023年10月1日的CSP-J复赛模拟赛，比赛中遇到四道题目，分别涉及字符串匹配、乘法算法、前缀和去重求和及点集操作。第一题和第二题在赛中完成，第三题和第四题赛中未解，赛后补题完成。总结中强调了比赛中思考的重要性，以及避免因失误和分心导致的扣分。
日期：2023年10月1日星期日
学号：S07731
姓名：魏仲毅
1.比赛概况：
比赛总分共4题，满分400。
赛时拿到130分，其中第一题100分，第二题30分，第三题0分，第四题0分。
2.比赛过程：
先想出第一题的思路,觉得第一题很简单,就把第一题写了。
第二题也很简单，但思路有一点问题（先加再乘，不是先乘再加）。
第三题用了前缀和来写，但是没有操作好桶与前缀和数组的关系。
第四题直接输出了一个样例，命运已经注定。
3.题解报告：
（每题下分重点，情况，题意，赛时想法，题解，AC代码。）
（1） 第一题：重复判断(repeat)
重点: 模拟。
情况：赛中AC（第一道AC，好棒）。
题意：小可需要判断一个字符串a，是否由另一个字符串b重复若干次得到的。
赛时本题做题想法：特判长度，模拟重复s2，判断是不是s1。
题解：考察基础的字符串匹配，j表示当前匹配到b字符串的第j位。i表示当前匹配到a字符串的第i位，两两比较，如果t=t.size()等于 ，说明一遍已经复制完了，从零开始重新匹配（题解中用取模表示这一效果）。
我的AC 代码：
#include<bits/stdc++.h>
using namespace std;
string s1,s2;
int main(){
//freopen("repeat.in","r",stdin);
//freopen("repeat.out","w",stdout);
int t;
cin>>t;
while(t--){
cin>>s1>>s2;
if(s1.size()%s2.size()!=0){
cout<<"NO"<<endl;
}
else{
string s3=s2;
while(s1.size()>s2.size()){
s2+=s3;
}
if(s1==s2){
cout<<"YES"<<endl;
}
else{
cout<<"NO"<<endl;
}
}
}
//fclose(stdin);
//fclose(stdout);
return 0;
}
题解代码：(可以对照题解来看)
#include<bits/stdc++.h>
using namespace std;
string a, b;
int main() {
int T;
cin >> T;
while(T--) {
bool flag = 0;
cin >> a >> b;
for(int i = 0, j = 0; i < a.size(); ++i) {
if(a[i] != b[j]) {
flag = 1;
break;
}
++j;
j %= b.size();
}
if(flag) puts("NO");
else puts("YES");
}
return 0;
}
（2） 第二题：歪果仁学乘法(multiplication)
重点：题目描述乘法思想。
情况：赛中30分，已补题。
题意：对于a × b：
1.将a，b的每一位上的数码画成线，不同位之间分隔开。
2.a 和 b 的方向垂直画出。
3.数出每个方向上交点的个数，即是 c 对应位置上的数码。
给出两个数字 a, b，求它们的乘积时交点的总个数是多少。
赛时本题做题想法：与正解有偏差，先乘再加，把a，b相乘，再数位分离（肯定是没好好看题。）
题解：先分解十位和个位，两两相乘后相加即可。
简单的AC 代码：
#include<bits/stdc++.h>
using namespace std;
int main(){
//freopen("multiplication.in","r",stdin);
//freopen("multiplication.out","w",stdout);
int a,b;
cin>>a>>b;
int q=a%10,w=b%10,e=a/10,r=b/10;
int sum=q*w+q*r+e*w+e*r;
cout<<sum;
//fclose(stdin);
//fclose(stdout);
return 0;
}
（3） 第三题：去重求和(summation)
重点：前缀和。
情况：赛中0分,已补题。
题意：小可有一个长度为 n 的序列ai。他定义sum(l,r),为a[l]~a[r],这些数去重之后的和。
请求出
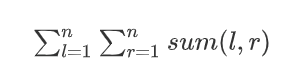
赛时本题做题想法：用前缀和去求，用桶去标记，遍历到多次出现就只加一次。
题解：开一个f数组求以i为终点的区间的和，求过一次就标记，最后累加起来即可。
本题AC 代码：
#include<bits/stdc++.h>
using namespace std;
const long long M=1e9+7;
map<long long,int> m;
long long n,a[1000005],f[1000005],sum;
int main(){
//freopen("summation.in","r",stdin);
//freopen("summation.out","w",stdout);
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<=n;i++){
f[i]=f[i-1]+a[i]*(i-m[a[i]]);
m[a[i]]=i;
}
for(int i=1;i<=n;i++) sum=(sum+f[i])%M;
cout<<sum;
//fclose(stdin);
//fclose(stdout);
return 0;
}
（4) 第四题：点集操作(point)
重点：邻接表。
情况：赛中0分，已补题。
题意：小可在学习图论，他有一个有向无环图，他想知道对这个图做任意次modify(i,j)操作之后的图中剩余的最小点数，其中1≤i,j≤n，其中modify(i,j)为一次操作：
1.任选不同的两个点i,j
2.称Ai为i能到达的所有点组成的点集，Aj为j能到达的所有点组成的点集 。（注意：每个点可以到达的点集包含这个点本身）
3.设 B 为一个最大的点集，满足B既是Ai的子集，又是Aj的子集 。
4.将 B 在图中变成一个新点，B 内的所有边全部删除。点集B以外的点与点集B以内的点的连边关系转移到新点上。
赛时本题做题想法：想暴力枚举，但是没有时间了。
题解：把有入度的相关点的重叠点，变成一个大点B，是一次modify操作。发现在一个单向链上，只需要让链头的两个点进行一次操作就可以将整个链变成两个点。所以每次操作可以在一条所含点数超过 2 的单向链上进行，直至不能继续操作，剩下的点的个数即为图中剩余的最小点数。
由上面操作的特殊性可以知道所有入度为 0 的点删不掉，所有满足所有入边对应点入度为 0 的点也删不掉，可以将这些点（所有满足所有入边对应点入度为 0 的点）看成新点。统计这些点个数即可。
以下为AC 代码：
#include<bits/stdc++.h>
using namespace std;
const int MAXN=1e6+5;
int n,m,x[MAXN*2],y[MAXN*2],in[MAXN];
int head[MAXN],num,ans;
bool b[MAXN],vis[MAXN];
vector<int>v;
struct node{
int to,next;
}e[MAXN*2];
void add(int u,int v){
e[++num].to=v;
e[num].next=head[u];
head[u]=num;
}
int main(){
cin >> n >> m;
for(int i=1;i<=m;++i){
cin >> x[i] >> y[i];
add(x[i],y[i])
in[y[i]]++;
}
for(int i=1;i<=n;++i){
if(!in[i]){
v.push_back(i);
ans++;
}
}
for(int i=1;i<=m;++i){
if(in[x[i]])b[y[i]]=1;
}
for(int i=0;i<v.size();++i){
for(int j=head[v[i]];j;j=e[j].next){
if(!b[e[j].to]){
b[e[j].to]=1;
ans++;
}
}
}
cout << ans;
return 0;
}
4. 赛后总结：
对这五天做一个小总结，结果如下：
1.考试时不要图快，要多花些时间思考，以防失误；
2.不要嘻嘻哈哈，容易错的很惨（比如第四天）；
3.集中注意力，不要分心，无论发生多搞笑的事都要专心作题，否则结果同第二条；
4.准备纸笔，打好草稿，不要空想；
5.上课好好学数学，否则模拟题完全没有思路（！！！）；
6.不要打字太快，谨防符号出差错；
7.不要乱搞电脑；
8.遇到自己写的代码中难以快速解释的，要注释，防止忘记和老师赛后让你讲题；
9.有别的方法，如果还有时间写的就写出来然后注释掉；
10.千万别抄答案，损人不利己的事别作；
11.实在想不出正解就骗分或者拿部分分，别耽误太多时间；
12.考试前先看卷子，按照难易程度决定写题顺序；
13.连骗分和拿部分分的方法都想不出来的话就先跳过；
14.如果想出正解但来不及写，就把能得分的最快方法写上；
15.超时不要紧，有分就行；
16.千万不要写旧版编译器不能用的代码，否则一旦算错申诉流程很长；
17.以认真的态度对待考试，不要不把考试当回事；
18.考不好别灰心，下次努力；
19.要积极，不要害怕考不好，发挥出你的真正实力；
20.以后的路还很长，不要紧张。
考试加油！
扫一扫
341
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
