【每日一题】【动态规划&二分】2022年2月9日-NC91 最长上升子序列(三)

描述
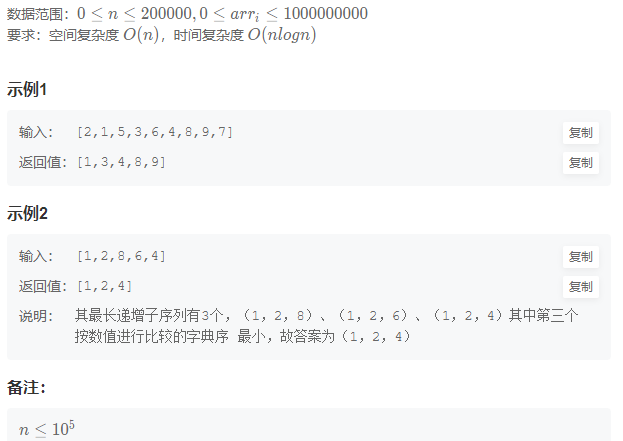
给定数组 arr ，设长度为 n ，输出 arr 的最长上升子序列。(如果有多个答案，请输出其中 按数值(注：区别于按单个字符的ASCII码值)进行比较的 字典序最小的那个)

方法1：双层循环实现动态规划-超时

import java.util.*;

public class Solution {
    /**
     * retrun the longest increasing subsequence
     * @param arr int整型一维数组 the array
     * @return int整型一维数组
     */
    public int[] LIS (int[] arr) {
        int n = arr.length;
        if (n == 0) {
            return null;
        }
        int[] dp = new int[n];
        int max = Integer.MAX_VALUE;
        int index = -1;
        Arrays.fill(dp, 1);
        for (int i = 1; i < n; i++) {
            for (int j = 0; j < i; j++) {
                if (arr[j] < arr[i]) {
                    dp[i] = Math.max(dp[i], dp[j] + 1);
                }
                if (dp[i] >= max) {
                    index = i;
                    max = dp[i];
                }
            }
        }
        //赋值
        int[] res = new int[max];
        for (int j = max, i = index; j > 0; i--) {
            if (dp[i] == j) {
                res[j--] = arr[i];
            }
        }
        return res;
    }
}

方法2：动态规划+二分查找，tail数组记录最小的数

import java.util.*;


public class Solution {
    /**
     * retrun the longest increasing subsequence
     * @param arr int整型一维数组 the array
     * @return int整型一维数组
     */
    public int[] LIS (int[] arr) {
        int n = arr.length;
        int[] dp = new int[n];
        int[] tail = new int[n + 1];
        int end = 0;
        tail[0] = Integer.MIN_VALUE; //存储对应位置元素的值
        for(int i = 0; i < n; i++) {
            int num = arr[i];
            if(tail[end] < num) {
                end++;
                tail[end] = num;
                dp[i] = end;
            } else {
                int low = 1, high = end;
                while(low <= high) {
                    int mid = low + ((high - low) >> 1);
                    if(tail[mid] >= num) {
                        high = mid - 1;
                    } else if(tail[mid] < num) {
                        low = mid + 1;
                    }
                }
                tail[low] = num;
                dp[i] = low;
            }
        }
        int[] res = new int[end];
        int len = end;
        for(int i = n - 1; i >= 0; i--) {
            if(dp[i] == len) {
                res[len - 1] = arr[i];
                len--;
            }
        }
        return res;
    }
}

方法3：方法2中二分查找使用工具类实现

import java.util.*;


public class Solution {
    /**
     * retrun the longest increasing subsequence
     * @param arr int整型一维数组 the array
     * @return int整型一维数组
     */
    public int[] LIS (int[] arr) {
        int n = arr.length;
        int[] dp = new int[n];
        int[] tail = new int[n + 1];
        int end = 0;
        tail[0] = Integer.MIN_VALUE; //存储对应位置元素的值
        for(int i = 0; i < n; i++) {
            int num = arr[i];
            if(tail[end] < num) {
                end++;
                tail[end] = num;
                dp[i] = end;
            } else {
                int site = Arrays.binarySearch(tail, 1, end, arr[i]);
                if(site >= 0) {
                    continue;
                }
                int ins = -(site + 1);
                tail[ins] = arr[i];
                dp[i] = ins;
            }
        }
        int[] res = new int[end];
        int len = end;
        for(int i = n - 1; i >= 0; i--) {
            if(dp[i] == len) {
                res[len - 1] = arr[i];
                len--;
            }
        }
        return res;
    }
}