P1908 逆序对 （归并排序，树状数组）

题目：https://www.luogu.com.cn/problem/P1908

solve1：归并排序
如何给一堆数字排序？
答：分成两半，先排左半边再排右半边，最后合并就行了，至于怎么排左边和右边，请重新阅读这句话。

归并排序就是递归将原来的序列不断二分，分到不能再分，然后将左右子区间排序合并（合并时左右区间各自都已经有序了）
得到逆序对的关键代码：
ans += mid - i + 1;

归并排序将左右区间合并时，左右区间已经是有序了的，所以只需要统计右区间中每一个数与左区间会产生多少逆序对就好了。
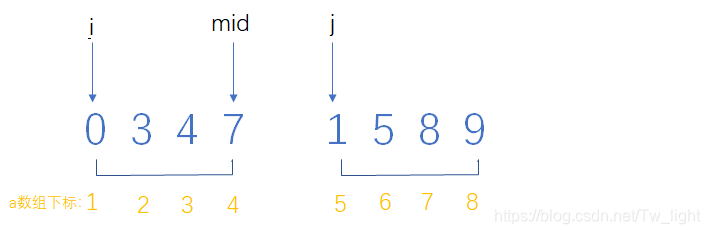
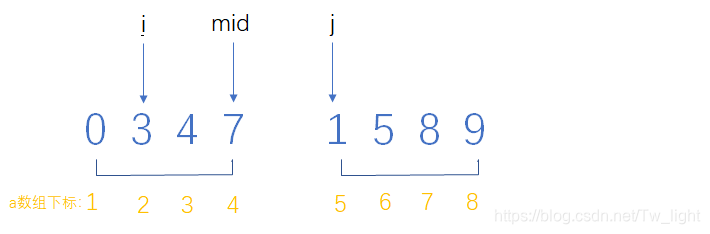
例如，将下面左右区间合并

i = 1， j = 5, mid = 4;

a[ i ] <= a[ j ]成立,（将a[ i ]放入temp数组）temp[ k++ ] = a[ i++ ]


i = 2;
a[ i ] <= a[ j ] 不成立，（将a[ j ]放入temp数组) temp[ k++ ] = a[ j++ ],
a[ j ] 与左区间形成的逆序对的对数 = mid - i + 1 = 4 - 2 + 1 = 3对，也就是a[ 5 ] 与 a [ 2 ], a [ 3 ], a [ 4 ] 分别会形成逆序对。

solve2:树状数组

我们要统计每一个数与前面所有的数会产生对少逆序对，最后相加就可以，但是怎么统计呢？

可以考虑建树状数组，树状数组是是一种用于高效处理对一个存储数字的列表进行更新及求前缀和的数据结构。

初始树状数组为0，每出现一个数字就更新树状数组，在相应的位置+1。当第i个数$a_i$出现时，前面 i-1 个数已经在树状数组中记录过了，树状数组内比$a_i$大的都会与之形成逆序对，由于前 i-1 个数一定先出现，所以产生的逆序对数为 i - query($a_i$)

code1:归并排序

#include<iostream>
#include<algorithm>
#include<cstring>
#include<string>
#include<cstdio>
using namespace std;
const int INF = 0x3f3f3f3f;
const int MAXN = 5e5 + 7;
#define ll long long int
ll ans;
int n;
int a[MAXN];
int temp[MAXN];
void mergSort(int l, int r)
{
    if(l == r) return ;
    int i, j, k;
    int mid = (l + r) >> 1;
    i = l, j = mid + 1, k = l;
    mergSort(l, mid); //左边有序
    mergSort(mid + 1, r);//右边有序

    while(i <= mid && j <= r) //左右合并
    {
        if(a[i] <= a[j])
            temp[k++] = a[i++];
        else
        {
            temp[k++] = a[j++];
            ans += mid - i + 1;
        }
    }
    while(i <= mid)
        temp[k++] = a[i++];
    while(j <= r)
        temp[k++] = a[j++];
    for(int u = l; u <= r; u++)
        a[u] = temp[u];
}
int main()
{
    scanf("%d", &n);
    for(int i = 1; i <= n; i++)
        scanf("%d", &a[i]);

    mergSort(1, n);
    printf("%lld\n",ans);
    return 0;
}

code2:树状数组

#include<iostream>
#include<algorithm>
#include<cstring>
#include<string>
#include<cstdio>
using namespace std;

const int INF = 0x3f3f3f3f;
const int MAXN = 5e5 + 7;
int c[MAXN], id[MAXN];
#define ll long long int
ll ans;
int n;
struct point
{
    int num, val;
}a[MAXN];
bool cmp(point p, point q)
{
    if(p.val == q.val) return p.num < q.num;
    return p.val < q.val;
}
void upData(int i, int v)
{
    for(; i <= n; i += (i & (-i)))
        c[i] += v;
}
int query(int i)
{
    int ans = 0;
    for(; i; i -= (i & (-i)))
        ans += c[i];
    return ans;
}
int main()
{
    scanf("%d", &n);
    for(int i = 1; i <= n; i++)
        scanf("%d", &a[i].val), a[i].num = i; //第几个输入的数

    sort(a + 1, a + 1 + n, cmp);
    for(int i = 1; i <= n; i++)
        id[a[i].num] = i; //第a[i].num个输入的数排序后是第几大

    ll ans = 0;
    for(int i = 1; i <= n; i++)
    {
        upData(id[i], 1);
        ans += i - query(id[i]);
    }
    printf("%lld\n", ans);
    return 0;
}