红黑树详解：性质、插入操作与AVL树对比-优快云博客

本文链接：https://blog.youkuaiyun.com/TryMyBestToDo_/article/details/131640043

红黑树

红黑树是一种自平衡的二叉查找树，是一种高效的查找树。它是由 Rudolf Bayer 于1972年发明，在当时被称为对称二叉 B 树(symmetric binary B-trees)。后来，在1978年被 Leo J. Guibas 和 Robert Sedgewick 修改为如今的红黑树。红黑树具有良好的效率，它可在 O(logN) 时间内完成查找、增加、删除等操作。

红黑树的性质

学过二叉查找树的同学都知道，普通的二叉查找树在极端情况下可退化成链表，此时的增删查效率都会比较低下。为了避免这种情况，就出现了一些自平衡的查找树，比如 AVL，红黑树等。这些自平衡的查找树通过定义一些性质，将任意节点的左右子树高度差控制在规定范围内，以达到平衡状态。
红黑树是每个结点都带有颜色属性的二叉查找树，颜色或红色或黑色。在二叉查找树强制一般要求以外，对于任何有效的红黑树有如下额外要求:

节点是红色或黑色。
根是黑色。
所有叶子都是黑色（NIL 即 NULL节点）。
每个红色节点必须有两个黑色的子节点。（从每个叶子到根的所有路径上不能有两个连续的红色节点。）
从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点（简称黑高）。

有了上面的几个性质作为限制，即可避免二叉查找树退化成单链表的情况。
保证了任意节点到其每个叶子节点路径最长不会超过最短路径的2倍
当某条路径最短时，这条路径必然都是由黑色节点构成。当某条路径长度最长时，这条路径必然是由红色和黑色节点相间构成（性质4限定了不能出现两个连续的红色节点）。而性质5又限定了从任一节点到其每个叶子节点的所有路径必须包含相同数量的黑色节点。此时，在路径最长的情况下，路径上红色节点数量 = 黑色节点数量。该路径长度为两倍黑色节点数量，也就是最短路径长度的2倍。举例说明一下，请看下图：

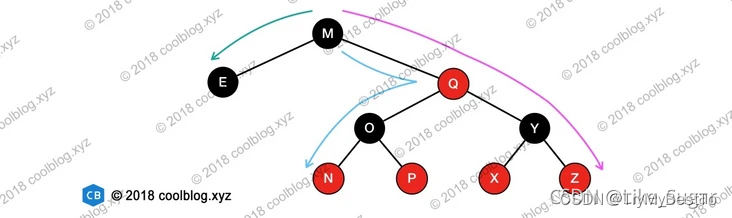
红黑树操作

旋转操作

旋转操作分为左旋和右旋，左旋是将某个节点旋转为其右孩子的左孩子，而右旋是节点旋转为其左孩子的右孩子。
针对M右旋转步骤（左旋转相反即可）：
- 将节点 M 的左孩子引用指向节点 E 的右孩子
- 将节点 E 的右孩子引用指向节点 M，完成旋转

private void rightRotate(RedBlackTreeNode node) {
    RedBlackTreeNode left = node.getLeft();
    RedBlackTreeNode parent = node.getParent();
    node.setLeft(left.getRight());
    if(left.getRight() != null){
        left.getRight().setParent(node);
    }
    node.setParent(left);
    left.setRight(node);
    if(parent == null){
        root = left;
        left.setParent(null);
    }else{
        left.setParent(parent);
        if(parent.getLeft() != null && parent.getLeft() == node){
            parent.setLeft(left);
        }else{
            parent.setRight(left);
        }
    }
}

插入操作

插入节点的默认颜色为红色，原因：
- 如果插入的节点是黑色，那么这个节点所在路径比其他路径多出一个黑色节点，这个调整起来会比较麻烦（参考红黑树的删除操作，就知道为啥多一个或少一个黑色节点时，调整起来这么麻烦了）。
- 如果插入的节点是红色，此时所有路径上的黑色节点数量不变，仅可能会出现两个连续的红色节点的情况。这种情况下，通过变色和旋转进行调整即可，比之前的简单多了。
插入过程和二叉查找树插入过程基本类似。
检测新节点插入后，红黑树的性质是否造到破坏（两个连续红色节点的情况）：
- 约定：cur为当前节点，p为父节点，g为祖父节点，u为叔叔节点。
  - 此处g祖父节点一定不为空：parent是红色的，则parent一定不是根节点，parent的双亲一定是存在的。

情况一：u叔叔节点存在且为红

注意:此处所看到的树，可能是一棵完整的树，也可能是一棵子树
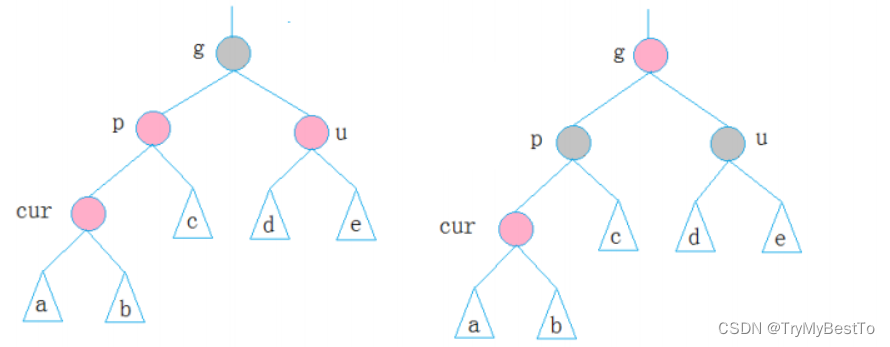
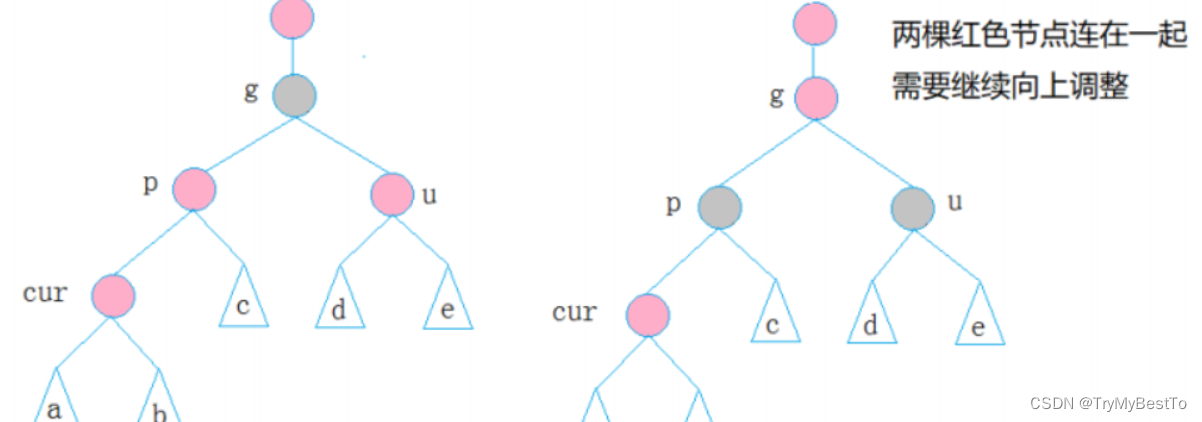
如果g是根节点，调整完成后，需要将g改为黑色
如果g是子树，g一定有双亲，且g的双亲如果是红色，需要继续向上调整

if(uncle != null && isRed(uncle)){
    setBlack(parent);
    setBlack(uncle);
    setRed(grandFather);
    node = grandFather;
    continue;
}

情况二：u不存在或为黑，p,g,cur在同一侧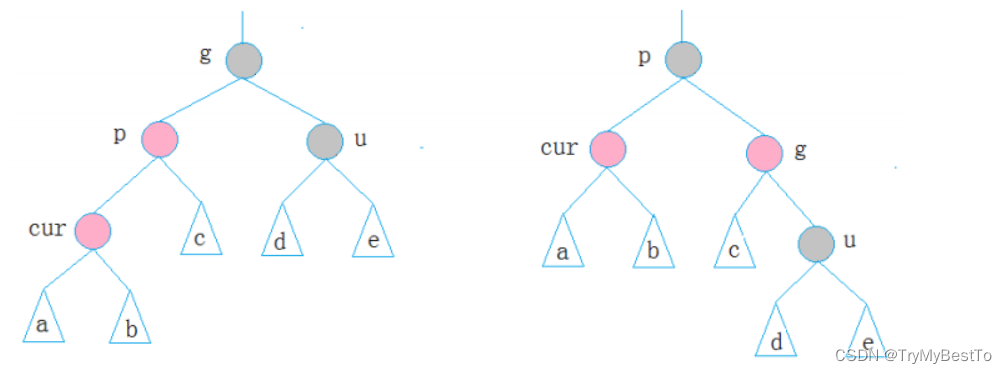

若都在左侧，则针对g进行右旋转，否则针对g进行左旋转
p、g变色=》p变黑，g变红

rightRotate(grandFather);
setBlack(parent);
setRed(grandFather);

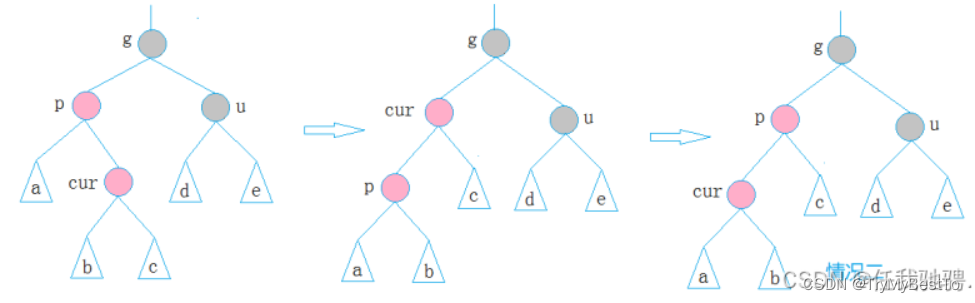
情况三：u不存在或为黑，p,g,cur不在同一侧

若cur为p的右子节点，则进行将左旋转
若cur为p的左子节点，则进行右旋转
此时就转换成了情况二

if(parent.getRight() == node){
    //插入节点为父节点的右子树
    //左旋
    leftRotate(parent);
    //将旋转后的parent看作插入节点
    RedBlackTreeNode tmp = node;
    node = parent;
    parent = tmp;
}

红黑树的验证

检测其是否满足二叉搜索树（中序遍历是否为有序序列）
检测其是否满足红黑树的性质

红黑树与AVL树的比较

红黑树和AVL树都是高效的平衡二叉树，增删改查的时间复杂度都是O(log2N)
红黑树不追求绝对平衡，只需保证最长路径不超过最短路径的2倍，相对而言，降低了插入和旋转的次数，所以在经常进行增删的结构中性能比AVL树更优。
而且红黑树实现比较简单，所以实际运用中红黑树更多。
完整Java代码：

public class RedBlackTree {
    //根节点
    private RedBlackTreeNode root;

    @Data
    class RedBlackTreeNode {
        public static boolean Red = false;
        public static boolean Black = true;
        //节点颜色
        private boolean color;
        private int data;
        private RedBlackTreeNode left;
        private RedBlackTreeNode right;
        private RedBlackTreeNode parent;

        public RedBlackTreeNode(int data){
            this.data = data;
            color = Red;
        }
    }

    /**
     * 插入节点
     * @param data
     * @return
     */
    public RedBlackTreeNode insert(int data){
        RedBlackTreeNode insert = new RedBlackTreeNode(data);
        if(root == null){
            root = insert;
            setBlack(insert);
        }else{
            RedBlackTreeNode parent = null;
            RedBlackTreeNode node = root;
            while(node != null){
                parent = node;
                if(node.getData() >= data){
                    //左子树
                    node = node.getLeft();
                }else{
                    //右子树
                    node = node.getRight();
                }
            }

            //跳出循环则说明找到插入位置
            if(parent.getData() >= data){
                parent.setLeft(insert);
            }else{
                parent.setRight(insert);
            }
            insert.setParent(parent);

            //旋转和调整节点颜色保持红黑树平衡
            insertFix(insert);
        }
        return insert;
    }

    /**
     * 旋转和调整节点颜色保持红黑树平衡
     * @param node 插入节点
     */
    private void insertFix(RedBlackTreeNode node) {
        while(node.getParent() != null && isRed(node.getParent())){
            RedBlackTreeNode parent = node.getParent();
            RedBlackTreeNode grandFather = parent.getParent();
            if(grandFather.getLeft() == parent){
                //F为G左儿子的情况
                RedBlackTreeNode uncle = grandFather.getRight();
                if(uncle != null && isRed(uncle)){
                    setBlack(parent);
                    setBlack(uncle);
                    setRed(grandFather);
                    node = grandFather;
                    continue;
                }
                if(parent.getRight() == node){
                    //插入节点为父节点的右子树
                    //左旋
                    leftRotate(parent);
                    //将旋转后的parent看作插入节点
                    RedBlackTreeNode tmp = node;
                    node = parent;
                    parent = tmp;
                }
                rightRotate(grandFather);
                setBlack(parent);
                setRed(grandFather);
                break;
            }else{
                //F为G的右儿子的情况，对称操作
                RedBlackTreeNode uncle = grandFather.getLeft();
                if(uncle != null && isRed(uncle)){
                    setBlack(parent);
                    setBlack(uncle);
                    setRed(grandFather);
                    node = grandFather;
                    continue;
                }
                if(parent.getLeft() == node){
                    //插入位置为父节点的左子树
                    //右旋
                    rightRotate(parent);
                    RedBlackTreeNode tmp = node;
                    node = parent;
                    parent = tmp;
                }
                setBlack(parent);
                setRed(grandFather);
                leftRotate(grandFather);
                break;
            }
        }
        setBlack(root);
    }

    /**
     * 删除节点
     * @param data
     * @return
     */
    public RedBlackTreeNode delete(int data){
        RedBlackTreeNode node = query(data);
        if(node == null){
            return null;
        }
        deleteNode(node);
        return node;
    }

    /**
     * 查询节点
     * @param data
     * @return
     */
    public RedBlackTreeNode query(int data){
        if(root == null){
            return null;
        }
        RedBlackTreeNode node = root;
        while(node != null){
            if(node.getData() == data){
                return node;
            }else if(node.getData() >= data){
                node = node.getLeft();
            }else {
                node = node.getRight();
            }
        }
        return null;
    }

    private void deleteNode(RedBlackTreeNode node) {
        if (node == null){
            return;
        }
        //替换节点
        RedBlackTreeNode replaceNode = null;
        if(node.getLeft() != null && node.getRight() != null){
            //存在左右子树
            RedBlackTreeNode tmp = node.getRight();
            while(tmp != null){
                replaceNode = tmp;
                tmp = tmp.getLeft();
            }
            //将替换节点的值放到原本需要删除的节点
            node.setData(replaceNode.getData());
            //删除替换节点
            node = replaceNode;
        }

        if(node.getLeft() != null){
            replaceNode = node.getLeft();
        }else{
            replaceNode = node.getRight();
        }
        RedBlackTreeNode parent = node.getParent();
        if(parent == null){
            root = replaceNode;
            if(replaceNode != null){
                replaceNode.setParent(null);
            }
        }else{
            if(parent.getLeft() == node){
                parent.setLeft(replaceNode);
            }else{
                parent.setRight(replaceNode);
            }
            if(replaceNode != null){
                replaceNode.setParent(parent);
            }
        }
        if(isBlack(node)){
            //replaceNode为了保持平衡，多了一个黑色，需修复
            removeFix(parent, replaceNode);
        }
    }

    /**
     * 修复
     * @param parent
     * @param node 多了一个黑色
     */
    private void removeFix(RedBlackTreeNode parent, RedBlackTreeNode node) {
        while(isBlack(node) && node != root){
            if(parent.getLeft() == node){
                //S是P的左儿子
                RedBlackTreeNode brother = parent.getRight();
                if(isRed(brother)){
                    setBlack(brother);
                    setRed(parent);
                    leftRotate(parent);
                    brother = parent.getRight();
                }
                if(brother == null || (isBlack(brother.getLeft()) && isBlack(brother.getRight()))){
                    setRed(brother);
                    node = parent;
                    parent = node.getParent();
                    continue;
                }
                if(isRed(brother.getLeft()) && isBlack(brother.getRight())){
                    setRed(brother);
                    setBlack(brother.getLeft());
                    rightRotate(brother);
                    brother = parent.getRight();
                }
                brother.setColor(parent.isColor());
                setBlack(parent);
                setBlack(brother.getRight());
                leftRotate(parent);
                node = root;
            }else{
                //S是P的右儿子
                RedBlackTreeNode brother = parent.getLeft();
                if(isRed(brother)){
                    setBlack(brother);
                    setRed(parent);
                    rightRotate(parent);
                    brother = parent.getLeft();
                }
                if(brother == null || (isBlack(brother.getLeft()) && isBlack(brother.getRight()))){
                    setRed(brother);
                    node = parent;
                    parent = node.getParent();
                    continue;
                }
                if(isRed(brother.getRight()) && isBlack(brother.getLeft())){
                    setBlack(brother.getRight());
                    setRed(brother);
                    leftRotate(brother);
                    brother = parent.getLeft();
                }
                brother.setColor(parent.isColor());
                setBlack(parent);
                setBlack(brother.getLeft());
                rightRotate(parent);
                node = root;
            }
        }
        if(node != null){
            setBlack(node);
        }
    }

    /**
     * 左旋
     * @param node
     */
    private void leftRotate(RedBlackTreeNode node) {
        RedBlackTreeNode right = node.getRight();
        RedBlackTreeNode parent = node.getParent();

        node.setRight(right.getLeft());
        if(right.getLeft() != null){
            right.getLeft().setParent(node);
        }
        node.setParent(right);

        right.setLeft(node);
        if(parent == null){
            root = right;
            right.setParent(null);
        }else{
            right.setParent(parent);
            if(parent.getLeft() != null && parent.getLeft() == node){
                parent.setLeft(right);
            }else{
                parent.setRight(right);
            }
        }
    }

    /**
     * 右旋
     * @param node
     */
    private void rightRotate(RedBlackTreeNode node) {
        RedBlackTreeNode left = node.getLeft();
        RedBlackTreeNode parent = node.getParent();

        node.setLeft(left.getRight());
        if(left.getRight() != null){
            left.getRight().setParent(node);
        }
        
        node.setParent(left);
        left.setRight(node);
        if(parent == null){
            root = left;
            left.setParent(null);
        }else{
            left.setParent(parent);
            if(parent.getLeft() != null && parent.getLeft() == node){
                parent.setLeft(left);
            }else{
                parent.setRight(left);
            }
        }
    }

    /**
     * 设置颜色为黑
     * @param node
     */
    public static void setBlack(RedBlackTreeNode node) {
        if(node == null){
            return;
        }else{
            node.setColor(RedBlackTreeNode.Black);
        }
    }

    /**
     * 设置颜色为红
     * @param node
     */
    public static void setRed(RedBlackTreeNode node) {
        if(node == null){
            return;
        }else{
            node.setColor(RedBlackTreeNode.Red);
        }
    }

    /**
     * 是否是黑色节点
     * @param node
     * @return
     */
    public static  boolean isBlack(RedBlackTreeNode node){
        if(node == null){
            return true;
        }else{
            return node.isColor() == RedBlackTreeNode.Black;
        }
    }

    /**
     * 是否是红色节点
     * @param node
     * @return
     */
    public static  boolean isRed(RedBlackTreeNode node){
        if(node == null){
            return false;
        }else{
            return node.isColor() == RedBlackTreeNode.Red;
        }
    }

    /**
     * 层级遍历
     * @param root
     */
    public static void levelTraversal(RedBlackTreeNode root){
        if(root == null){
            return;
        }
        Queue<RedBlackTreeNode> queue = new LinkedList<>();
        queue.offer(root);
        while(!queue.isEmpty()){
            RedBlackTreeNode poll = queue.poll();
            String color = "Black";
            if(isRed(poll)){
                color = "Red";
            }
            System.out.print(poll.getData()+"(" + color + ") ");
            if(poll.getLeft() != null){
                queue.offer(poll.getLeft());
            }
            if(poll.getRight() != null){
                queue.offer(poll.getRight());
            }
        }
    }

    /**
     * 前序遍历
     * @param node
     */
    public static void recursivelyPreTraversal(RedBlackTreeNode node){
        if(node == null){
            return;
        }
        String color = "Black";
        if(isRed(node)){
            color = "Red";
        }
        System.out.print(node.getData()+"(" + color + ") ");
        recursivelyPreTraversal(node.getLeft());
        recursivelyPreTraversal(node.getRight());
    }

    /**
     * 中序遍历
     * @param node
     */
    public static void recursivelyInTraversal(RedBlackTreeNode node){
        if(node == null){
            return;
        }
        recursivelyInTraversal(node.getLeft());
        String color = "Black";
        if(isRed(node)){
            color = "Red";
        }
        System.out.print(node.getData()+"(" + color + ") ");
        recursivelyInTraversal(node.getRight());
    }

    /**
     * 后序遍历
     * @param node
     */
    public static void recursivelyPostTraversal(RedBlackTreeNode node){
        if(node == null){
            return;
        }
        recursivelyPostTraversal(node.getLeft());
        recursivelyPostTraversal(node.getRight());
        String color = "Black";
        if(isRed(node)){
            color = "Red";
        }
        System.out.print(node.getData()+"(" + color + ") ");
    }
}