代码随想录算法训练营第三十六天 | 435. 无重叠区间，763. 划分字母区间，56. 合并区间

原创已于 2024-10-30 16:50:45 修改 · 608 阅读

4 ·

CC 4.0 BY-SA版权

文章标签：

#算法

于 2024-04-06 09:51:38 首次发布

文章讲述了三道编程题目，涉及重叠区间问题的解决方案，包括无重叠区间、划分字母区间和合并区间。重点介绍了左边界排序和贪心策略的应用，通过实例展示了如何利用这些方法优化处理区间问题。

今天的三道题目，都算是重叠区间问题，大家可以好好感受一下。都属于那种看起来好复杂，但一看贪心解法，惊呼：这么巧妙！

还是属于那种，做过了也就会了，没做过就很难想出来。

不过大家把如下三题做了之后，重叠区间基本上差不多了

435. 无重叠区间

题目讲解：代码随想录

重点：

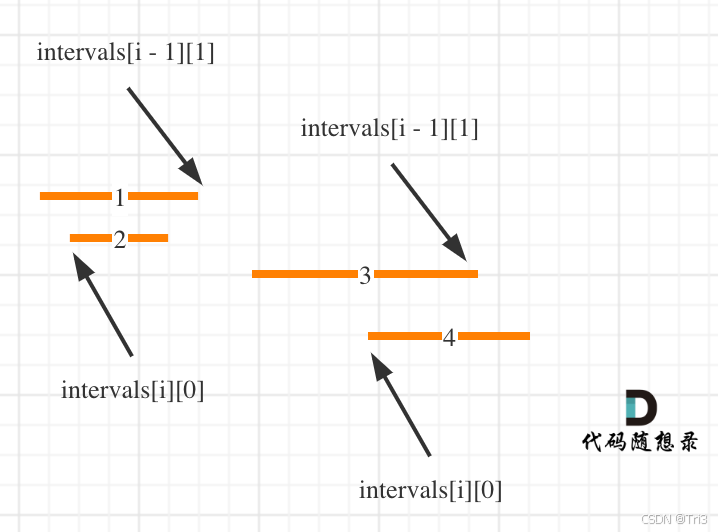
左边界排序我们就是直接求重叠的区间，count为记录重叠区间数。

贪心算法：

局部最优：把最长的移除。全局最优：移除了最少数量的重叠区间。

思路：

1. 按左边界排序
Arrays.sort(intervals, Comparator.comparingInt(a -> a[0]));
2. 遍历区间数组，发生了重叠就result++，更新最小右边界
int result = 0;
for (int i = 1; i < intervals.length; i++) {
    // 当前区间与上一个区间发生了重叠
    if (intervals[i][0] < intervals[i - 1][1]) {
        result++;
        // 把当前区间右边界更新为最小右边界
        intervals[i][1] = Math.min(intervals[i][1], intervals[i - 1][1]);
    }
}

public int eraseOverlapIntervals(int[][] intervals) {
    // 没必要给右边界排序，因为重叠的时候会按照最小的右边界取
    Arrays.sort(intervals, Comparator.comparingInt(a -> a[0]));
    int result = 0;
    for (int i = 1; i < intervals.length; i++) {
        // 当前区间与上一个区间发生了重叠
        if (intervals[i][0] < intervals[i - 1][1]) {
            result++;
            // 把当前区间右边界更新为最小右边界
            intervals[i][1] = Math.min(intervals[i][1], intervals[i - 1][1]);
        }
    }
    return result;
}

763. 划分字母区间

题目讲解：代码随想录

重点：

1. 在遍历的过程中相当于是要找每一个字母的边界，如果找到之前遍历过的所有字母的最远边界，说明这个边界就是分割点了。此时前面出现过所有字母，最远也就到这个边界了。

可以分为如下两步：

统计每一个字符最后出现的位置
从头遍历字符，并更新字符的最远出现下标，如果找到字符最远出现位置下标和当前下标相等了，则找到了分割点

思路：

1. 记录每个字母的最远下标
int[] lastIndex = new int[27];
for (int i = 0; i < s.length(); i++) {
    lastIndex[s.charAt(i) - 'a'] = i;
}
2. 遍历，寻找当前区间的起始和终止下标
for (int i = 0; i < s.length(); i++) {
    // 寻找当前区间的最大的最远下标
    endIndex = Math.max(endIndex, lastIndex[s.charAt(i) - 'a']);
    // 到当前区间末尾
    if (i == endIndex) {
        result.add(endIndex - startIndex + 1);
        startIndex = endIndex + 1;
    }
}

public List<Integer> partitionLabels(String s) {
    // 记录每个字母的最远下标
    int[] lastIndex = new int[27];
    for (int i = 0; i < s.length(); i++) {
        lastIndex[s.charAt(i) - 'a'] = i;
    }
    ArrayList<Integer> result = new ArrayList<>();
    // 记录当前区间的起始和终止下标
    int startIndex = 0, endIndex = 0;
    for (int i = 0; i < s.length(); i++) {
        // 寻找当前区间的最大的最远下标
        endIndex = Math.max(endIndex, lastIndex[s.charAt(i) - 'a']);
        // 到当前区间末尾
        if (i == endIndex) {
            result.add(endIndex - startIndex + 1);
            startIndex = endIndex + 1;
        }
    }
    return result;
}

56. 合并区间

本题相对来说就比较难了。

题目讲解：代码随想录

重点：

本题的本质其实还是判断重叠区间问题。本题是判断区间重贴后要进行区间合并。

思路：

1. 按照左边界排序，并且初始化记录合并区间的左边界和右边界
List<int[]> res = new LinkedList<>();
Arrays.sort(intervals, Comparator.comparingInt(a -> a[0]));

int curStart = intervals[0][0];
int curRightMostBound = intervals[0][1];
2. 遍历区间数组，没有发现重叠则加入res并更新记录的左边界和右边界，发现重叠则只更新记录的右边界
for (int i = 1; i < intervals.length; i++) {
    if (intervals[i][0] > curRightMostBound) {
        res.add(new int[]{curStart, curRightMostBound});
        curStart = intervals[i][0];
        curRightMostBound = intervals[i][1];
    } else {
        curRightMostBound = Math.max(curRightMostBound, intervals[i][1]);
    }
}

public int[][] merge(int[][] intervals) {
    List<int[]> res = new LinkedList<>();
    // 按照左边界排序
    Arrays.sort(intervals, Comparator.comparingInt(a -> a[0]));
    // 记录正在合并区间的左区间和右区间
    int curStart = intervals[0][0];
    int curRightMostBound = intervals[0][1];
    for (int i = 1; i < intervals.length; i++) {
        // 如果当前遍历到的区间已经不重叠
        if (intervals[i][0] > curRightMostBound) {
            // 把上一个区间保存进res，并重置合并区间的记录
            res.add(new int[]{curStart, curRightMostBound});
            curStart = intervals[i][0];
            curRightMostBound = intervals[i][1];
        // 如果当前遍历到的区间还是重叠，更新合并区间的右区间为最大区间
        } else {
            curRightMostBound = Math.max(curRightMostBound, intervals[i][1]);
        }
    }
    // 把最后一个合并区间加入res
    res.add(new int[]{curStart, curRightMostBound});
    return res.toArray(new int[res.size()][]);
}