网络流四·最小路径覆盖

最新推荐文章于 2024-05-08 19:14:17 发布

原创最新推荐文章于 2024-05-08 19:14:17 发布 · 3.9k 阅读

9 ·

CC 4.0 BY-SA版权

常用简单算法专栏收录该内容

23 篇文章

订阅专栏

H市一共有N个旅游景点(编号1..N)，由M条单向游览路线连接。在一个景点游览完后，可以顺着游览线路前往下一个景点。

为了避免游客重复游览同一个景点，游览线路保证是没有环路的。

每一个调查团可以从任意一个景点出发，沿着计划好的游览线路依次调查，到达终点后再返回。每个景点只会有一个调查团经过，不会重复调查。

举个例子：

上图中一共派出了3个调查团：

1. 蓝色：调查景点；2

2. 橙色：调查景点；1->3->4->6

3. 绿色：调查景点；5->7

当然对于这个图还有其他的规划方式，但是最少也需要3个调查团。

由于小组内的人数有限，所以大家希望调查团的数量尽可能少，同时也要将所有的景点都进行调查。

输入

第1行：2个整数N,M。1≤N≤500,0≤M≤20,000。

第2..M+1行：2个数字u,v，表示一条有向边(u,v)。保证不会出现重复的边，且不存在环。

输出

第1行：1个整数，表示最少需要的调查团数量。

样例输入

样例输出

提示：最小路径覆盖

对于一条路径，起点的入度为0，终点的出度为0，中间节点的出入度都为1。

每一个点最多只能有1个后继，同时每一个点最多只能有1个前驱。

假如我们选择了一条边(u,v)，也就等价于把前驱u和后继v匹配上了。这样前驱u和后继v就不能和其他节点匹配。

利用这个我们可以这样来构图：

将每一个点拆分成2个，分别表示它作为前驱节点和后继节点。将所有的前驱节点作为A部，所有后继节点作为B部。

接下来进行连边，若原图中存在一条边(u,v)，则连接A部的u和B部的v。

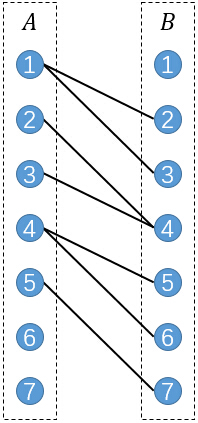
在这个上面做一个最大二分匹配：

其中实线表示被选中的匹配，虚线表示未被选中的。

有没有发现，和原图刚好有着对应的关系。

这样在匹配结束的时候，我们就可以直接通过匹配的情况来确定选中的路径。

但是如何保证这样就能得到最小的路径覆盖呢？

如果一个点是路径起点的话，它在B部的节点一定是没有匹配上的。

经过最大匹配算法后，B部剩下没有被匹配的点一定是最少的，也就对应了最小需要的路径数。

所以最小路径覆盖的结果才是N-最大匹配数。

正是这样，这样问题也就解决了。接下来第二个问题，怎么用网络流来解决二分匹配呢？

上一次我们讲了二分多重匹配，二分匹配不就是它的简化版么。

只需要把源点s到A部的边和B部到汇点t的边容量限定为1就可以了！

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
#define MAX 1010
#define MAXCF 101
#define min(a,b) (a)>(b)?(b):(a)
using namespace std;

int cf[MAX][MAX];//存储图
int queue[MAX];//搜索队列
int path[MAX];//保存路径
int capacity[MAX];//流量数组，保存经过该点的最小流量
bool visited[MAX];//记录访问数组

int findAugmentPath(int T)
{
	int i = 0, tail = 0;
	memset(visited, 0, sizeof(visited));

	queue[tail] = 1;//将源点加入队列
	capacity[1] = MAXCF;
	visited[1] = true;
	while (i <= tail)
	{
		int u = queue[i];
		if (u == T)
			return capacity[T];//找到一条增广路径，返回该路径最小流量
		for (int v = 2; v <= T; v++)
		{
			if (!visited[v] && cf[u][v] > 0)
			{
				path[v] = u;
				capacity[v] = min(cf[u][v], capacity[u]);//记录路径上的最小残余流量
				visited[v] = true;
				tail++;
				queue[tail] = v;
			}
		}
		i++;
	}
	return 0;
}

void modifyGraph(int T)
{
	int flow = capacity[T];
	int now = T;
	while (now != 1)
	{
		int fa = path[now];
		cf[fa][now] -= flow;
		cf[now][fa] += flow;
		now = fa;
	}
}

int main()
{
	int N, M;
	int i, j;
	int u, v;

	while (cin >> N >> M)
	{
		int S = 1;
		int E = S + N + N + 1;
		int result = 0;
		memset(cf, 0, sizeof(cf));
		for (i = 0; i < N; ++i)
		{
			cf[S][S + i + 1] = 1;
			cf[S + N + i + 1][E] = 1;
		}
		for (i = 0; i < M; ++i)
		{
			cin >> u >> v;
			cf[S + u][S + N + v] = 1;
		}

		int maxFlow = 0;
		int delta = 0;
		while (delta = findAugmentPath(E))
		{
			maxFlow += delta;
			modifyGraph(E);
		}
		cout << N - maxFlow << endl;
		
	}
	return 0;
}