智能优化算法
遗传算法
Genetic Algorithm,简称GA
-
基本思想:
- 根据问题的目标函数构造适值函数Fitness Function
- 产生一个初始种群
- 根据适值函数的好坏,不断的进行选择繁殖
- 若干代后得到适值函数最好的个体即为最优解。
-
构成要素:
-
种群 population 种群大小 pop-size
-
种群表达法 – 编码方法
-
遗传算子 genetic operator
交叉 crossover 变异 mutation
交叉率高,解空间大,但计算时间较长
-
选择策略
一般为正比选择
选择种群中适值高的个体,适者生存
-
停止准则
一般是指定最大迭代次数
-
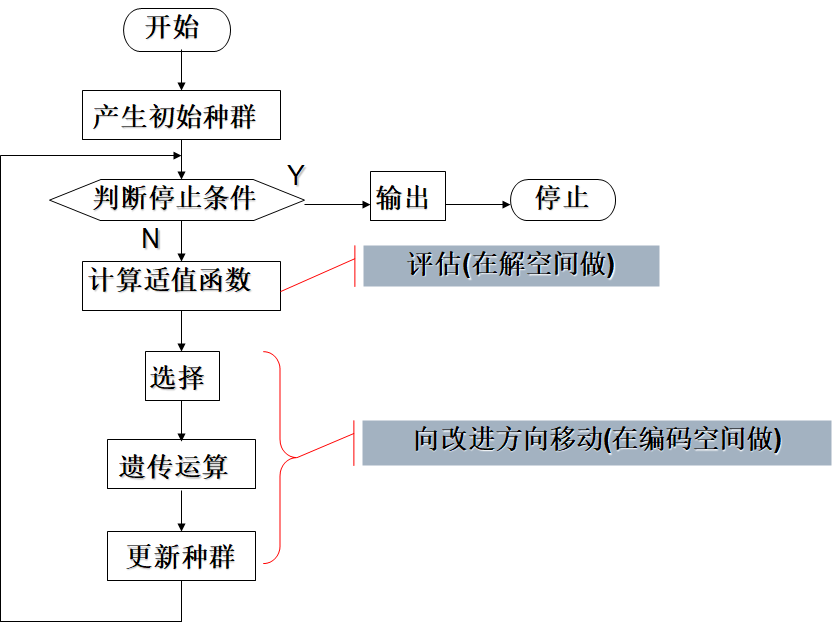
-
解空间与编码空间的转换
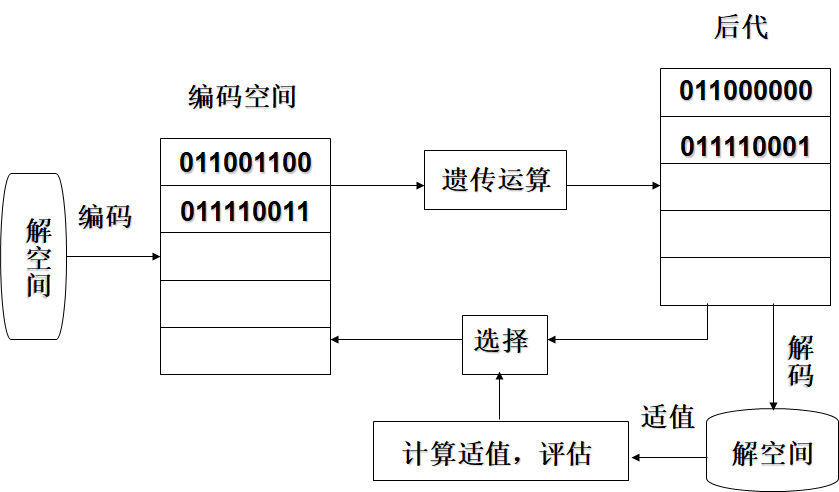
各个步骤实现
- 初始种群的产生
- 编码方法
- 适值函数
- 遗传算法
- 选择策略
- 停止准则
Δ\DeltaΔ 初始种群的产生
随机产生(依赖于编码方法);种群的大小(依赖于计算机的计算能力和计算复杂度)。
例:0,1编码
产生ζi∈U(0,1)\zeta_i\in U(0,1)ζi∈U(0,1)
ζi>0.5,xi=1;\zeta_i>0.5,\quad x_i=1;ζi>0.5,xi=1;
ζi<0.5,xi=0;\zeta_i<0.5,\quad x_i=0;ζi<0.5,xi=0;
Δ\DeltaΔ 编码方法 --二进制编码
二进制编码,用0,1字符串表达
背包问题:0表示不取,1表示取
特点:
精度高时编码较长,一般不采用此法而用实值函数
编码长不利于计算
便于位值计算,包括的实数范围大
Δ\DeltaΔ 适值函数–根据目标函数设计
用适值函数F(x)F(x)F(x)标定目标函数f(x)f(x)f(x)采用 **-minf(x)**和 manf(x)
Δ\DeltaΔ 遗传运算–选择、交叉、变异
★\bigstar★ 交叉 Crossover
♡\heartsuit♡ 单切点交叉
随机产生一个断点 [1,n−1][1,n-1][1,n−1]
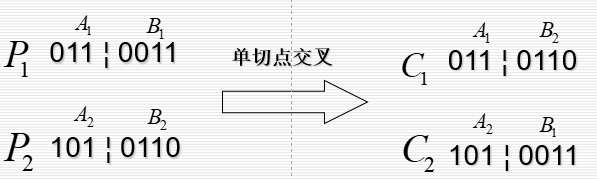
♡\heartsuit♡ 双切点交叉

★\bigstar★ 变异 Mutation
初始种群中没有需要的基因,在种群中按变异概率 Pm\ P_m Pm任选若干位基因改变位值0→1或1→0,
有意想不到的结果, Pm\ P_m Pm一般设定得比较小,在5%以下。
★\bigstar★ 选择
最常用的正比选择
对于个体iii,适值FiF_iFi,选择概率如下公式计算
Pi=Fi∑1NPFi
P_i={F_i \over{\sum_{1}^{NP}F_i}}
Pi=∑1NPFiFi
NP−−NumberofPopulation NP--Number of Population NP−−NumberofPopulation
之后采用轮盘赌的方法进行选择:
令PP0=0,PPi=∑j=1iPjPP_0=0,PP_i=\sum_{j=1}^{i} P_jPP0=0,PPi=∑j=1iPj
随机产生 εi∈U(0,1)\varepsilon_i \in U(0,1)εi∈U(0,1)
当 PPi≤εi≤PPiPP_i \le \varepsilon_i \le PP_iPPi≤εi≤PPi,选择个体 iii,
粒子群算法
Particle Swarm Optimization
-
基本思想
-
粒子群算法q粒子群算法的思想源于对鸟群捕食行为的研究
-
模拟鸟集群飞行觅食的行为,鸟之间通过集体的协作使群体达到最优目的,是一种基于Swarm Intelligence的优化方法。
-
马良教授在他的著作《蚁群优化算法》一书的前言中写到:
“自然界的蚁群、鸟群、鱼群、羊群、牛群、蜂群等,其实时时刻刻都在给予我们以某种启示,只不过我们常常忽略了大自然对我们的最大恩赐!…”
-
-
算法介绍
- 每个寻优的问题解都被想像成一只鸟,称为“粒子”。所有粒子都在一个D维空间进行搜索。
- 所有的粒子都由一个fitness function 确定适应值以判断目前的位置好坏。
- 每一个粒子必须赋予记忆功能,能记住所搜寻到的最佳位置。
- 每一个粒子还有一个速度以决定飞行的距离和方向。这个速度根据它本身的飞行经验以及同伴的飞行经验进行动态调整。
细说PSO
D维空间中,有N个粒子;
粒子iii位置:xi=(xi1,xi2,⋯xiD)x_i=(x_{i1},x_{i2},\cdots x_{iD})xi=(xi1,xi2,⋯xiD),将xix_{i}xi代入适应函数f(xi)f(x_i)f(xi)求适应值;
粒子iii速度:vi=(vi1,vi2,⋯viD)v_i=(v_{i1},v_{i2},\cdots v_{iD})vi=(vi1,vi2,⋯viD)
粒子iii个体经历过的最好位置:pbesti=(pi1,pi2,…piD)pbest_i=(p_{i1},p_{i2},…p_{iD})pbesti=(pi1,pi2,…piD)
种群所经历过的最好位置:gbest=(g1,g2,…gD)gbest=(g_1,g_2,…g_D)gbest=(g1,g2,…gD)
通常,在第d(1≤d≤D)d(1≤d≤D)d(1≤d≤D)维的位置变化范围限定在[Xmin,d,Xmax,d][X_{min, d},X_{max,d}][Xmin,d,Xmax,d]内,速度变化范围限定在[−Vmin,d,Vmax,d][-V_{min,d},V_{max,d}][−Vmin,d,Vmax,d]内(即在迭代中若vid,xidv_{id},x_{id}vid,xid超出了边界值,则该维的速度或位置被限制为该维最大速度或边界位置)
-
粒子iii的第ddd维速度更新公式:
vidk=ωvidk−1+c1r1(pbestid−xidk−1)+c2r2(gbestd−xidk−1) v_{id}^{k}=\omega v_{id}^{k-1}+c_1r_1(pbest_{id}-x_{id}^{k-1})+c_2r_2(gbest_d-x_{id}^{k-1}) vidk=ωvidk−1+c1r1(pbestid−xidk−1)+c2r2(gbestd−xidk−1) -
粒子iii的第ddd维位置更新公式
xidk=xidk−1+vidk−1 x_{id}^{k}=x_{id}^{k-1}+v_{id}^{k-1} xidk=xidk−1+vidk−1
vidkv_{id}^{k}vidk–表示第kkk次迭代粒子iii飞行速度的矢量的第ddd维分量xidkx_{id}^{k}xidk–表示第kkk次迭代粒子iii位置矢量的第ddd维分量
c1,c2c_1,c_2c1,c2–表示加速度常数,调节学习最大步长
r1,r2r_1,r_2r1,r2–表示两个随机函数,取值范围为[0,1][0,1][0,1],以增加搜索随机性
www–表示惯性 权重,非负数,调节对解空间的搜索范围
算法流程
1.Initial:
初始化粒子群体(群体规模为n),包括随机位置和速度。
2.Evaluation:
根据fitness function ,评价每个粒子的适应度。
3.Find the Pbest:
对每个粒子,将其当前适应值与其个体历史最佳位置(pbest)对应的适应值做比较,如果当前的适应值更高,则将用当前位置更新历史最佳位置pbest。
4.Find the Gbest:
对每个粒子,将其当前适应值与全局最佳位置(gbest)对应的适应值做比较,如果当前的适应值更高,则将用当前粒子的位置更新全局最佳位置gbest。
5.Update the Velocity:
根据公式更新每个粒子的速度与位置。
6.如未满足结束条件,则返回步骤2
通常算法达到最大迭代次数GmaxG_{max}Gmax或者最佳适应度值的增量小于某个给定的阈值时算法停止。
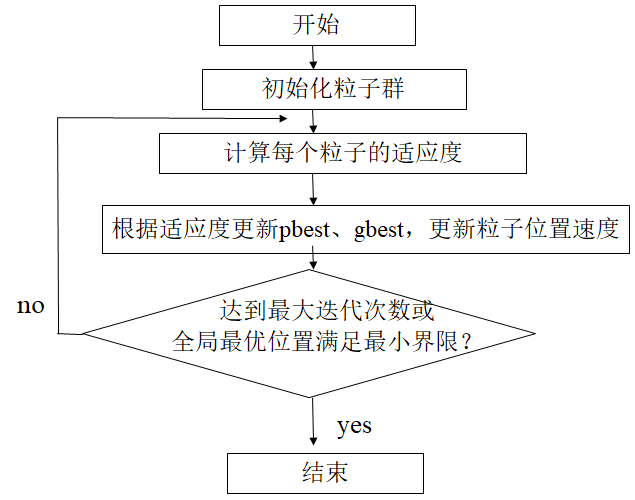
-
构成要素 群体大小mmm
mmm是一个整型参数,mmm很小时,陷入局部最优解的可能性就越大;mmm很大时,pso的优化能力很好。当群体数目增长至一定水平时,再增长将不再有显著的作用。
-
权重因子

-
最大速度 VmV_mVm
在于维护算法的探索能力与开发能力的平衡
VmV_mVm较大时额,探索能力增强,但粒子容易飞过最优解;VmV_mVm较小时,开发能力增强,但容易陷入局部最优解;因此VmV_mVm一般设为每维变量变化范围的10%−20%10\%-20\%10%−20%
-
邻域的拓扑结构
-
将群体内所有个体都作为粒子的邻域
-
只将群体中的部分个体作为粒子的邻域
邻域拓扑结构→决定\rightarrow^{决定}→决定群体历史最优解
因此,将粒子群算法分为 全局粒子群算法和局部粒子群算法
-
全局粒子群算法
- 粒子自己历史最优解
- 粒子群体的全局最优解
-
局部粒子群算法
- 粒子自己历史最优解
- 粒子邻居内粒子的最优解
邻域随迭代次数的增加线性变大,最后邻域拓展到整个粒子群。
-
-
-
粒子空间的初始化
较好地选择粒子空间的初始化空间,将大大缩短收敛时间,初始化空间根据具体问题的不同而不同,也就是说这是问题依赖的。
算法流程
-
在初始化范围内,对粒子群进行随机初始化,包括随机位置和速度
-
计算每个粒子的适应值
-
更新粒子个体的历史最优位置
-
更新粒子群体的历史最优位置
-
更新粒子的速度和位置,公式如下:
vk+1=c0vk+c1ξ(pk−xk)+c2η(pk−xk) v_{k+1}=c_0v_k+c_1\xi (p_k-x_k)+c_2\eta(p_k-x_k) vk+1=c0vk+c1ξ(pk−xk)+c2η(pk−xk)xk+1=xk+vk+1 x_{k+1}=x_k+v_{k+1} xk+1=xk+vk+1
-
若未达到终止条件,则转第二步
惯性权重 $\omega $
描述的是粒子上一代速度对当前速度的影响,ω\omegaω较大时,全局寻优能力强,局部寻优能力弱;反之,则局部寻优能力强。当问题空间较大时,为了在搜索速度沙河搜索精度之间达到平衡,通常是使算法在前期有较高的全局搜索能力以得到合适的种子,而在后期有较高的局部搜索能力以提高收敛精度。
w=wmax−(wmax−wmin)×runrunmax
w=w_{max}-(w_{max-w_{min}})\times {run\over run_{max}}
w=wmax−(wmax−wmin)×runmaxrun
wmax最大惯性权重,wmin最小惯性权重,run当前迭代次数,runmax为算法迭代总次数w_{max}最大惯性权重,w_{min}最小惯性权重,run当前迭代次数,run_{max}为算法迭代总次数wmax最大惯性权重,wmin最小惯性权重,run当前迭代次数,runmax为算法迭代总次数






















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










