【BZOJ - 3832】[Poi2014] Rally

---

@Description@

给定一个N个点M条边的有向无环图，每条边长度都是1。
请找到一个点，使得删掉这个点后剩余的图中的最长路径最短。

Input
第一行包含两个正整数$N,M(2<=N<=500000,1<=M<=1000000)$，表示点数、边数。
接下来M行每行包含两个正整数$A[i],B[i](1<=A[i],B[i]<=N,A[i]̸=B[i])$，表示A[i]到B[i]有一条边。

Output
包含一行两个整数x,y，用一个空格隔开，x为要删去的点，y为删除x后图中的最长路径的长度，如果有多组解请输出任意一组。

Sample Input
6 5
1 3
1 4
3 6
3 4
4 5
Sample Output
1 2

@Solution - Part 1@

【先膜拜想出来这道题的大佬们 orz】
【太神了，要我一辈子都想不出来这种题QAQ】
首先处理图不连通的情况：建立超级源点 s 向所有入度为 0 的点连边，建立超级汇点 t 使所有出度为 0 的点向 t 连边。

然后看一张图：

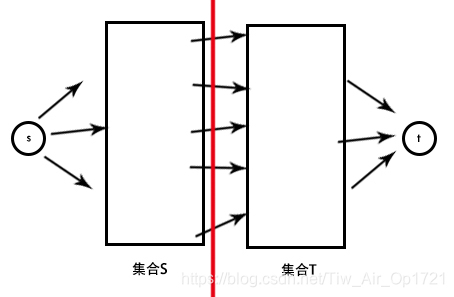
红线是该图的一个“割”：将红线上的边删除过后，原图形成两个连通块且两个连通块分别包含源点 s 与汇点 t 。
我们令包含源点 s 的连通块为集合 S，包含汇点 t 的为集合 T。

为什么要画这样一条“割”呢？可以发现有这样一个性质：原图中 s 到 t 的每一条路径恰好包含“割”上的一条边。
反过来，我们可以令一条边的 tag = “经过这条边的路径长度的最大值”，再用一个数据结构存储“割”上的所有边的 tag。
然后——假如我们要求解删去某一条“割”边的最长路，等价于在数据结构中删除这条边的 tag 后，求数据结构中的最大 tag。

删去某一个点，等价于删除它所有的入边。

这个数据结构应该支持（1）加入与删除（2）求最大值。
可以用堆，也可以像我一样直接用 multiset【常数大但好写www】。

也就是说：我们只需要使得“割”经过一个点的所有入边，就可以在 O(log n) 时间内求解删去某一个点的答案。

@Solution - Part 2@

具体来讲，我们怎么使得“割”经过一个点的入边呢？
可以用拓扑序来进行这个过程。

我们按照拓扑序，依此遍历每一个结点。
对于一个结点 i：先将它所有的入边从“割”中删除，求“割”中的最大值，再将它所有的出边加入“割”。

为什么这样是对的？

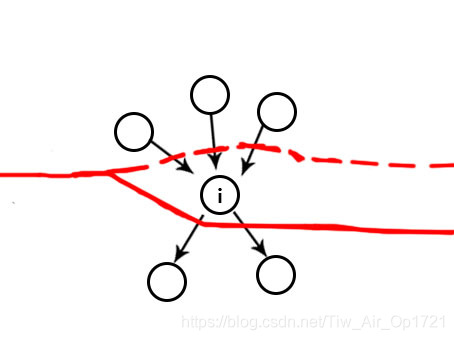
首先：可以发现这样操作以后，“割”仍然合法。
然后：因为是按照拓扑序进行的，所以 i 的入边连接的点 j 在之前一定已经处理过了。i 的入边作为 j 的出边，在处理 j 的时候就会加入“割”，所以 i 的所有入边此时肯定是在“割”内的。

所以这样是正确的。

@Some Details@

怎么求解一条边(u, v)的 tag？
可以用 DAG 上 dp 处理出 s 到 u 的最长路与 v 到 t 的最长路。

记住 s, t 是虚点，所以要消除它们对答案的影响。

可能出现这种情况：删除一个点所有的入边后，s 和 t 不连通了！
这时候的最长路 = max(s到集合S中的点的最长路, 集合T中的点到t的最长路)
【还记得集合S和T吗？不记得往上翻一翻】
再开两个堆来维护即可。

@Code@

在 bzoj 上能过，但是在本地 T 得很惨。
建议大家还是写一写带删除的堆吧。

#include<set>
#include<queue>
#include<cstdio>
#include<vector>
#include<algorithm>
using namespace std;
const int MAXN = 500000;
const int MAXM = 1000000;
const int INF = (1<<30);
int read() {
	int x = 0, f = 1; char ch = getchar();
	while( (ch > '9' || ch < '0') && ch != '-' ) ch = getchar();
	if( ch == '-' ) {f = -1; ch = getchar();}
	while( '0' <= ch && ch <= '9' ) {x = x*10 + ch-'0'; ch = getchar();}
	return x * f;
}
struct edge{
	int to;
	edge *nxt;
}edges[2*MAXM + 5], *adj[MAXN + 5], *ecnt;
int n, m, idg[MAXN + 5], odg[MAXN + 5];
int tp[MAXN + 5], tcnt = 0;
vector<int>G[MAXN + 5];
multiset<int, greater<int> >S, T, E;
void init() {
	ecnt = &edges[0];
	for(int i=0;i<=n+1;i++) {
		adj[i] = NULL;
		G[i].clear();
		idg[i] = odg[i] = 0;
	}
	S.clear(); T.clear(); E.clear();
}
void addedge(int u, int v) {
	edge *p = (++ecnt);
	p->to = v, p->nxt = adj[u], adj[u] = p;
	G[v].push_back(u);
}
void tpsort() {
	tcnt = 0;
	for(int i=0;i<=n+1;i++)
		idg[i] = 0;
	for(int i=0;i<=n+1;i++)
		for(edge *p=adj[i];p!=NULL;p=p->nxt)
			idg[p->to]++;
	queue<int>que; que.push(0);
	while( !que.empty() ) {
		int f = que.front(); que.pop(); tp[tcnt++] = f;
		for(edge *p=adj[f];p!=NULL;p=p->nxt)
			if( !(--idg[p->to]) ) que.push(p->to);
	}
}
int f[MAXN + 5], g[MAXN + 5];
int GetAnswer() {
	int ret = 0;
	if( !S.empty() )
		ret = max(ret, *S.begin());
	if( !T.empty() )
		ret = max(ret, *T.begin());
	if( !E.empty() )
		ret = max(ret, *E.begin());
	return ret;
}
void solve() {
	n = read(), m = read(); init();
	for(int i=1;i<=m;i++) {
		int u, v;
		u = read(), v = read();
		addedge(u, v);
		idg[v]++; odg[u]++;
	}
	for(int i=1;i<=n;i++) {
		if( !idg[i] ) addedge(0, i);
		if( !odg[i] ) addedge(i, n+1);
	}
	tpsort(); f[0] = g[n+1] = 0;
	for(int i=1;i<=n+1;i++) {
		f[tp[i]] = 0;
		for(int j=0;j<G[tp[i]].size();j++)
			f[tp[i]] = max(f[tp[i]], f[G[tp[i]][j]] + 1);
	}
	for(int i=n;i>=0;i--) {
		g[tp[i]] = 0;
		for(edge *p=adj[tp[i]];p!=NULL;p=p->nxt)
			g[tp[i]] = max(g[tp[i]], g[p->to] + 1);
	}
	for(int i=0;i<=n+1;i++)
		T.insert(g[i]-1);
	int ans = INF, num;
	for(int i=0;i<=n+1;i++) {
		for(int j=0;j<G[tp[i]].size();j++)
			E.erase(E.find(f[G[tp[i]][j]]+g[tp[i]]-1));
		T.erase(T.find(g[tp[i]]-1));
		if( tp[i] != 0 && tp[i] != n+1 ) {
			int x = GetAnswer();
			if( x < ans ) ans = x, num = tp[i];
			else if( x == ans && num > tp[i] ) num = tp[i];
		}
		for(edge *p=adj[tp[i]];p!=NULL;p=p->nxt)
			E.insert(f[tp[i]]+g[p->to]-1);
		S.insert(f[tp[i]]-1);
	}
	printf("%d %d\n", num, ans);
}
int main() {
	solve();
}

@End@

就是这样，新的一天里，也请多多关照哦(ノω<。)ノ))☆.。