6.2 感知器

感知器的概念由 罗森布拉特·弗兰克 在1957年提出，它是一种监督训练的二元分类器。

一、单层感知器

考虑一个只包含一个神经元的神经网络。

这个神经元有两个输入x1，x2，权值为w1，w2。其激活函数为符号函数：

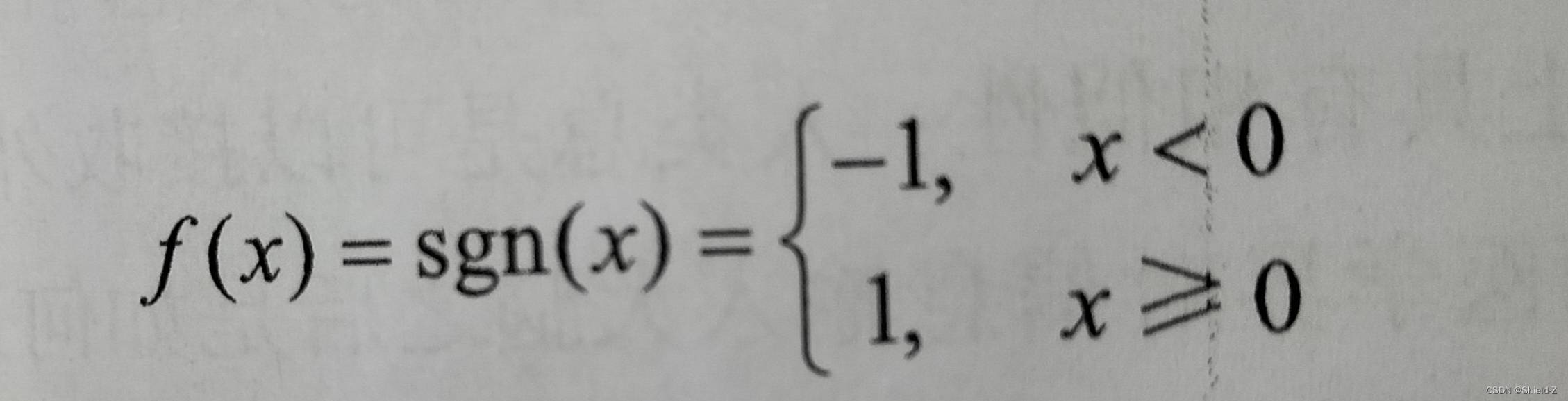
根据感知器训练算法，在训练过程中，若实际输出的激活状态 o 与预期输出的激活状态 y 不一致，则权值按以下方式更新：

w ' ← w + α · ( y - o ) · x

其中，w ' 为更新后的权值，

w为原权值，

y为预期输出，

x为输入，

α为学习率。

学习率既可以为固定值，也可以在训练中进行适应性的调整。

例如：

我们设定学习率 α = 0.01，把权值初始化为 w1 = -0.2，w2 = 0.3

若有训练样例 x1 = 5、x2 = 2；y=1，则实际输出与期望输出不一致：

 o = sgn（-0.2 * 5 + 0.3 * 2）= -1

因此对权值进行调整：

w1 = -0.2 + 0.01 * 2 * 5 = -0.1

w2 = 0.3 + 0.01 * 2 * 2 = 0.34

直观上来说，权值更新向着损失减小的方向进行，即网络的实际输出 o 越来越接近预期的输出 y 。在这个例子中我们看到，经过以上一次权值更新之后，这个样例输入的实际输出 

0 = sgn（-0.1 * 5 + 0.34 * 2）= 1，已经与正确的输出一致。

我们只需要对所有的训练样例重复以上的步骤，直到所有的样本都得到正确的输出即可。

二、多层感知器

单层感知器可以拟合一个超平面 y = ax₁ + bx₂，适合于线性可分的问题，而对于线性不可分的问题则无能为力。考虑异或函数作为函数的情况：

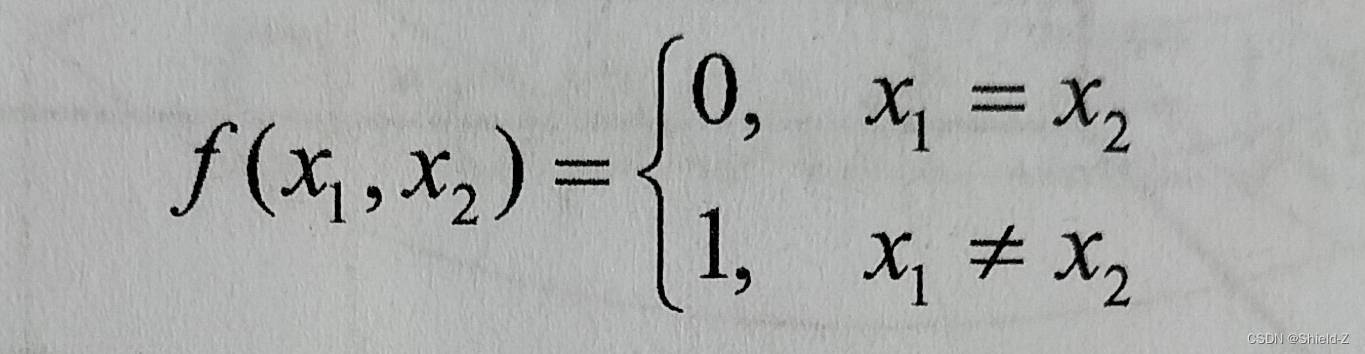
异或函数需要两个超平面才能进行划分。由于单层感知器无法克服线性不可分的问题，引入了多层感知器（Multi-Layer Perceptron，MLP），实现了异或运算，如图：

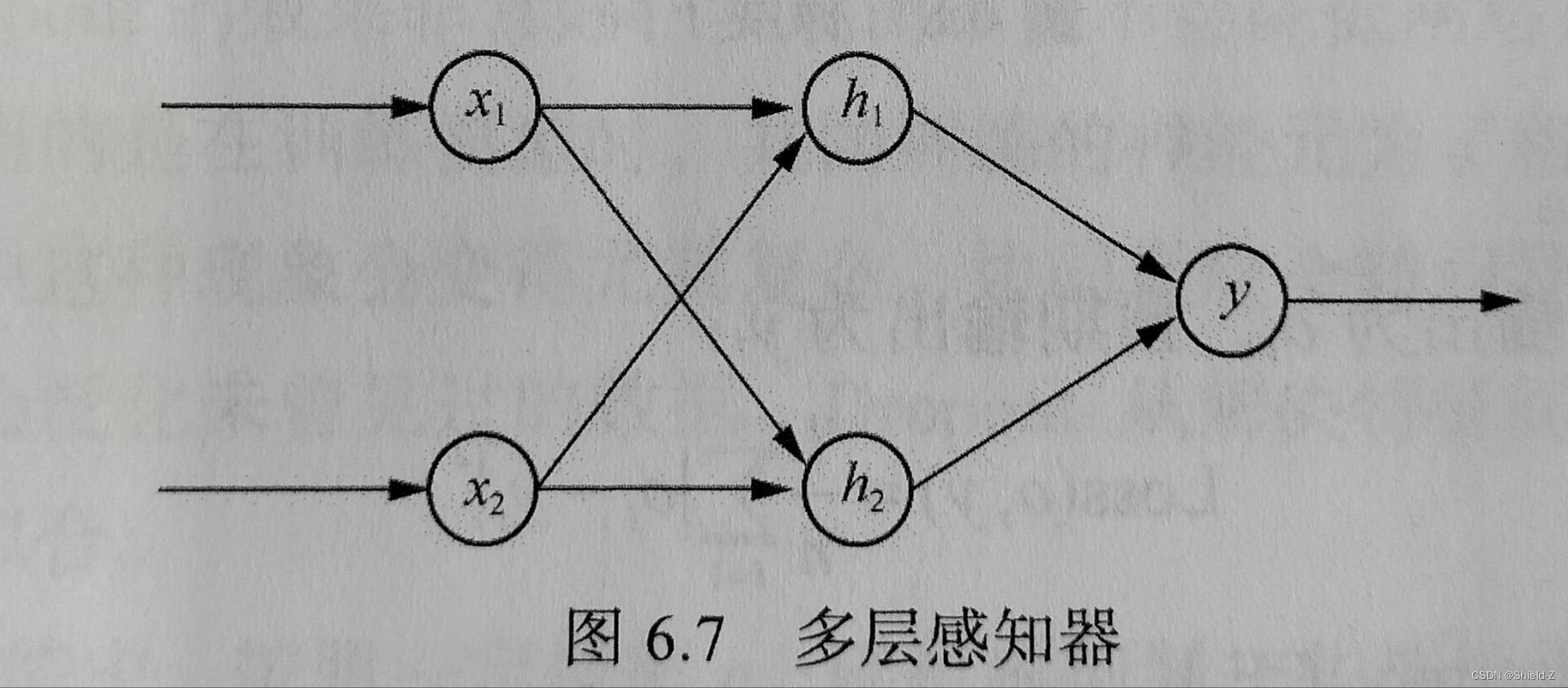
图中的隐藏层神经元 h₁ ，h₂ 相当于两个感知器，分别构造一个超平面