2.1 Perceptron Hypothesis Set 感知假说集及演算
感知假说集这部分,林老师主要是举了个线性回归的例子,来帮我们感性地认识了 h 这个东西到底是什么。
比如说线性回归:
以上说明了h是一个假设空间集,我们希望在h里面能找到一个g,使它最接近f。
这里f是指存在的一种理想化的规律或模式,是我们不知道的,但是我们的data都是依照这种模式产生的;因为f我们不知道,但是我们有data,所以我们可以根据data来找一个g,使g这个函数在我们已知的data上表现的尽可能像f这个理想化的函数。
那么如何用几何的方式来描述上述过程呢?
我们知道w,x都可以描述成向量形式,尽管他们可能不是二维的,我们为了方便起见,假设它们都是二维的。
当实际的为+1,而预测的
为-1时,我们更新
,

可以看到,这里的向量加法,是让,更新后的
,更偏向x这条向量线(
与更新后的
的夹角变小)。
当实际的为-1,而预测的
为+1时,我们更新
,

可以看到,这里的向量加法,是让,更新后的
,更远离
这条向量线(
与更新后的
的夹角变大)。
2.2 PLA算法流程
1、假设训练数据集是线性可分的
input:training data
output:
(1)选取初始值
(2)从训练集选取样本
(3)如果 ,更新
(4)转至(2)知道训练集样本被全部正确分类。
2.3 Guarantee of PLA
1、PLA收敛的一个必要条件是数据是线性可分的,也就是存在某个完美的使得
预测正确的时候:
为完美超平面对应的法向量
式(1)
通常以两个向量的内积的大小反应两个向量的越接近(但是仍需要考虑向量模大小,这里事实可以反应相似度)
更新 则有
式(2)
可以发现随着错误的更新不断地增大,可能是向量的模在增大,或者是夹角的余弦越来越大。
预测错误的时候有:
式(3)
此时
式(4)
这里,start from = 0, after
mistake corrections,有:
式(5)
由式(2)有
则有
迭代有
式(6)
其中表示迭代次数
表示转置
由式(4)有
即
式(7)
根据式 (5) 及式(6)式(7)
所以
式(8)
因为
式(9)
式(10)
式(11)
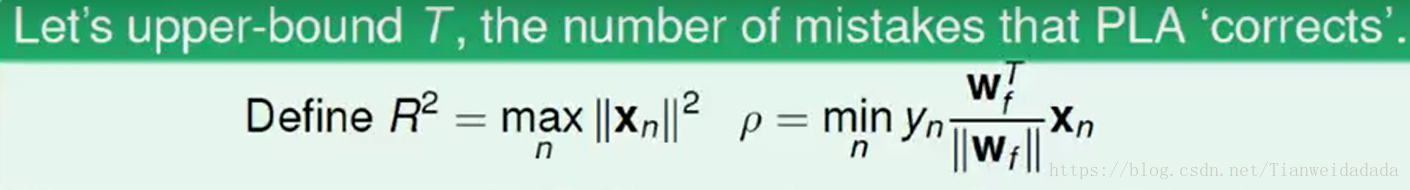
所以
2.4优缺点
优点:速度快,代码简单。
缺点:算法进行之前不知道数据是否可分,不知道什么时候可以终止。
参考:
https://blog.youkuaiyun.com/hulingyu1106/article/details/51212632 PLA 训练过程
https://blog.youkuaiyun.com/sjz_hahalala479/article/details/81003517 PLA 证明






 本文深入探讨了感知机假说集的概念,解释了如何在假设空间中寻找最佳函数逼近未知的理想模式。通过几何方式描述了感知机的学习过程,并详细介绍了PLA算法的工作流程和收敛保证,最后分析了其优缺点。
本文深入探讨了感知机假说集的概念,解释了如何在假设空间中寻找最佳函数逼近未知的理想模式。通过几何方式描述了感知机的学习过程,并详细介绍了PLA算法的工作流程和收敛保证,最后分析了其优缺点。
















 705
705

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








