机器学习总结：决策树

决策树算法我们并不陌生，可以看做是if-then规则的集合，那么决策树算法的关键在于如何确定每次if的条件是最优的。

ID3 C4.5

信息熵是信息论里的概念，其表达式如下所示：

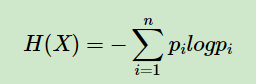
熵表征的是事物的混乱程度，熵越大，混乱程度越大。
信息增益：

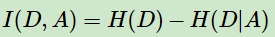
其表达式比较易懂，由信息熵减去减去特征A条件下D的条件熵，这也比较好理解，其实就是在A条件下数据集D不确定性的减少程度。显然，可以表征不同特征对于分类的能力。ID3算法就是对所有的特征进行信息增益的计算，找到当前最佳的特征作为if的条件。
以信息增益作为划分训练数据集的特征，存在偏向于选择取值较多的特征的问题。因此使用信息增益比对这一问题进行校正。
信息增益比的表达式如下：

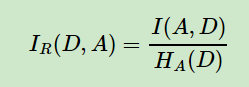
定义为其信息增益与训练数据集D源于特征A的值的熵之比，C4.5算法即为利用信息增益比作为特征的划分依据。

CART树（分类回归树classification and regression tree）

回归树采用平方误差最小化的准则进行特征选择，生成二叉树。具体的求解下式，得到最优切分变量A和最优切分点s。

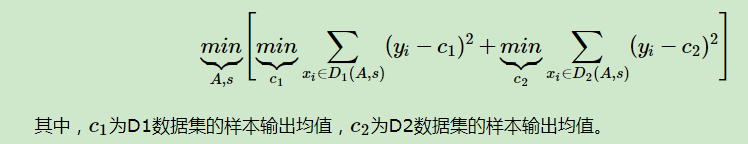
接着对每个区域重复上述的划分过程。直到满足条件为止。

分类树采用基尼指数最小化准侧进行特征选择，生成二叉树。基尼指数的表达式为

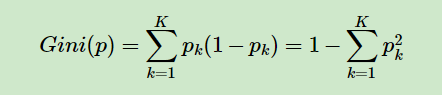
基尼指数代表了模型的不纯度，基尼指数越小，不纯度越低，特征越好。
对于样本D，如果特征A的某个值a，把D分为D1和D2两部分，则在特征A的条件下，D的基尼指数表达式为：

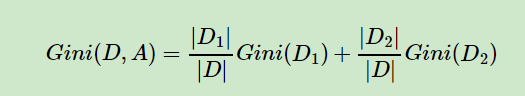
树的剪枝

剪枝主要有两种方式：预剪枝和后剪枝
预剪枝：在决策树的生成过程中，对每个节点再划分前先进行估计，若当前节点不能带来决策树泛化性能的提升，则停止划分。
后剪枝：先生成一颗完整的决策树，然后自底向上的对非叶节点进行考虑，若将该节点子树替换成叶子节点能带来泛化性能的提升，则将该子树替换为叶子节点。
这里说的泛化性能提升的评价标准其实是损失函数，对于C4.5来说是经验熵。
对于CART树来说，分类树是基尼系数，回归树是均方误差。

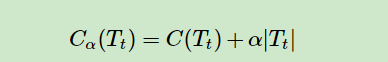
公式的图片来自于刘建平老师的博客