理解递归

什么是递归

递归（英语：Recursion），在数学与计算机科学中，是指在函数的定义中使用函数自身的方法。

什么时候用递归

如果一个问题满足以下三个条件，就可以考虑使用递归来解决：

1. 可以分解为一个或多个子问题；
2. 该问题和其子问题之间，只是数据规模不同，但解法是一样的；
3. 一定存在终止条件，使问题不能继续分解；

我们以求解某个正整数的阶乘为例来说明。已知求阶乘的公式为：
$$n!=n\ast (n-1)\ast (n-2)\ast ...\ast 1$$ 。那么这个问题，如何用递归思想来解决呢？根据公式，我们可以看出，其实求n的阶乘可以转化为求n-1的阶乘，因为$$n!=n\ast (n-1)!$$同理求n-1的阶乘，也可以转化为求n-2的阶乘，如此分解下去，直到n=1的时候，无法继续往下分解，递推终止，用一个公式统一表达:
$$f(n)=\{\begin{array}{l}1，n=1\\ n\ast f(n-1)，n>1\end{array}$$
用代码来描述就是：

 //利用递归求正整数n的阶乘
 int factorial(int n){
        if(n == 1) return 1;
        return n * factorial(n-1);
 }

递归的优缺点

优点

代码简洁高效。

缺点及解决办法

通过递归求解问题虽然代码简洁，但是有两个特别容易出现的问题：重复计算和栈溢出。

1. 重复计算

以求斐波那契数为例，假如我们要得到斐波那契数列中的第n个数，其递归求解公式如下：
$$f(n)=\{\begin{array}{l}1，n=1\\ 1，n=2\\ f(n-1)+f(n-2)，n>2\end{array}$$
这里写个测试用例，演示一下:

public class FibonacciTest {

    private int count = 0;

    public int fibonacci(int n){
        count++;
        if(n == 1) return 1;
        if(n == 2) return 1;
        return fibonacci(n-1)+ fibonacci(n-2);
    }

    public static void main(String[] args) {
        for(int i = 1; i <= 40; i++){
            FibonacciTest recursionTest = new FibonacciTest();
            System.out.format("n=%-2s,result=%-10s,count=%-10s\n",i,recursionTest.fibonacci(i),recursionTest.count);
        }
    }
}

执行结果如下：

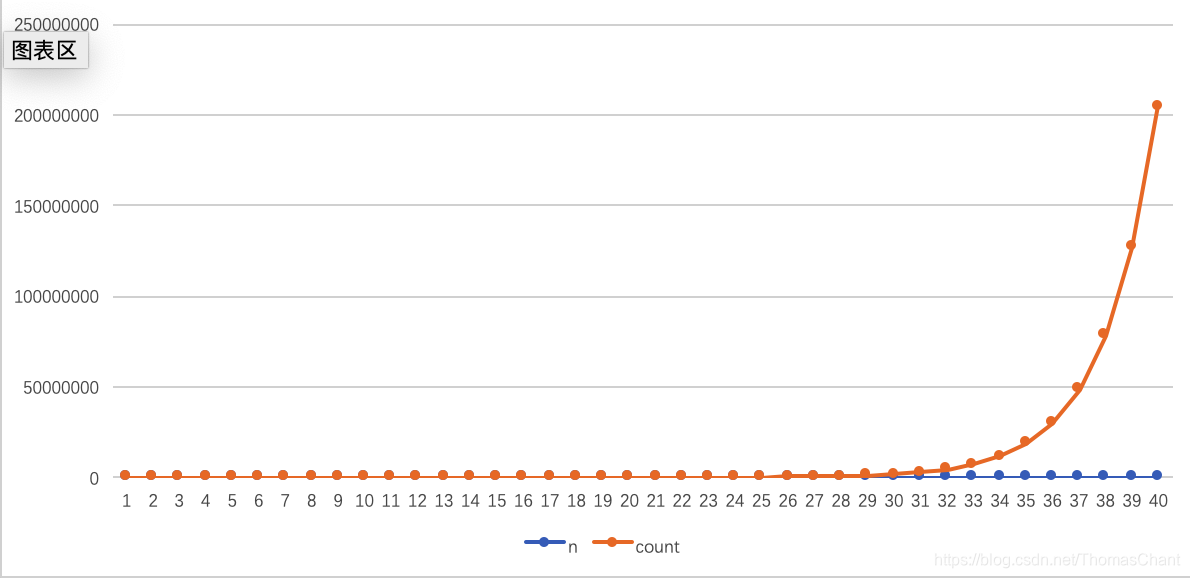
从执行可以看出，函数调用次数是在指数级增长的，在求第40个斐波那契数的时候，函数调用竟然达到了2亿多次，计算时间开始以秒计，性能急剧下降，到求第50个斐波那契数的时候，计算时间已经长到无法忍受了。原因就在于将一个问题分解成多个子问题后，每个子问题又分解成多个子子问题，如此一来，需要求解的问题总数是以指数级增长的。我们看一下递归求解第5个斐波那契数的分解过程

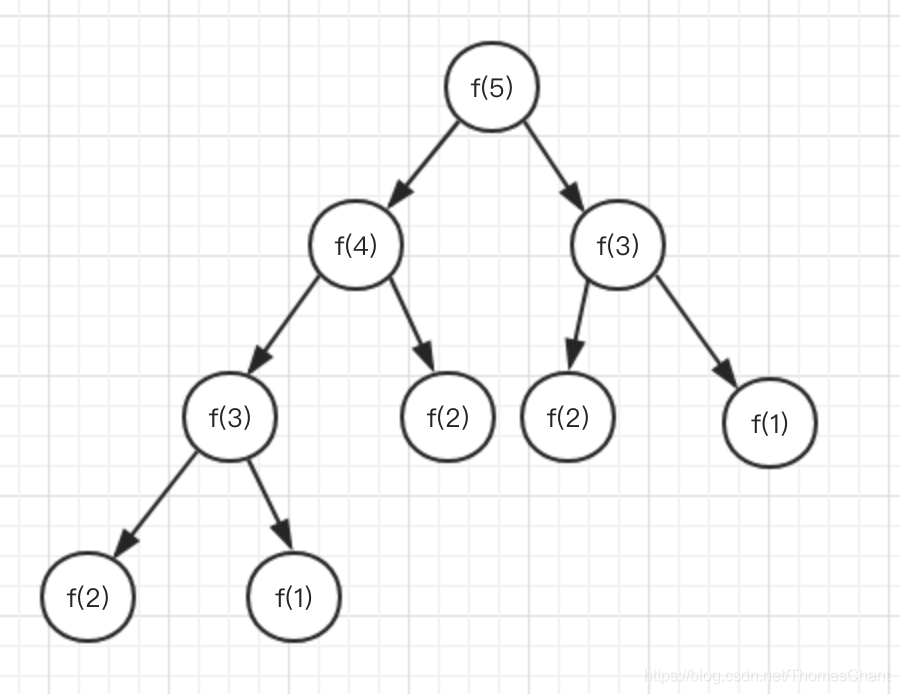
那么如何能避免这个问题呢？其实从上图可以看出，很多斐波那契数是重复计算了的，比如f(3),f(2),f(1)，其实这些问题只需要计算一次，然后缓存起来，就可以极大的改善性能。改进后的代码如下：

public class FibonacciCacheTest {

     private int count = 0;
     private Map<Integer,Long> valueCache = new HashMap<>();


     public long fibonacci(int n){
         count++;
         if(valueCache.containsKey(n)){
             return valueCache.get(n);
         }
         if(n == 1) return 1;
         if(n == 2) return 1;
         long v = fibonacci(n-1)+ fibonacci(n-2);
         valueCache.put(n, v);
         return v;
     }

     public static void main(String[] args) {
        for(int i = 1; i <= 50; i++){
            FibonacciCacheTest fibonacciTest1 = new FibonacciCacheTest();
            System.out.format("n=%-2s,result=%-12s,count=%-12s\n",i,fibonacciTest1.fibonacci(i),fibonacciTest1.count);
        }
    }
}

执行结果如下图所示

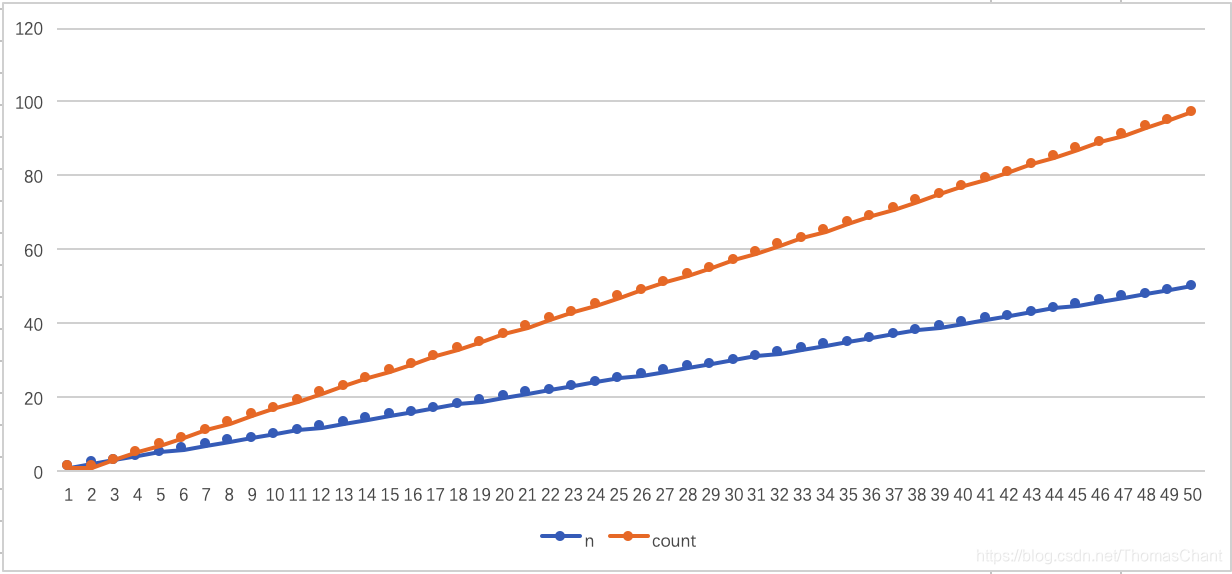
可以看出改进后，执行次数是线性增长的，性能得到了很大提升。

2. 栈溢出

接着我尝试增大n的值，当n=7175时（这个值是虚拟机栈内存分配有关，每个人不大一样），jvm虚拟机抛了一个错误：StackOverflowError，这是因为递归过程中申请的栈深度已经超出了虚拟机所能分配的最大栈深度。对于java虚拟机，可以通过-Xss参数适当增大虚拟机栈内存容量，从而间接增大栈的深度。

总结

本文主要讲解了如何使用递归以及使用递归时候应如何避免栈溢出和重复计算的问题。