一.冒泡排序
冒泡排序,就是每次比较,大的元素往后挪,比较完第一遍后,最大的元素排到了数组的最后一位 。第二次比较,还是从第一个元素开始和后面的比较,把剩余的最大的元素拍到数组的倒数第二位,第一轮比较的最大元素不参与比较 。
程序实现:
/*冒泡排序*/
public class Sort1 {
public int[] sort(int[] nums){
int temp = 0;
for(int i = 0; i < nums.length-1; i++){
for(int j = 0; j < nums.length-1-i; j++){
if(nums[j] > nums[j+1]){
temp = nums[j+1];
nums[j+1] = nums[j];
nums[j] = temp;
}
}
}
return nums;
}
}
二.快速排序
关键词:基准点放中间,两个哨兵头碰头
快速排序的核心思想就是找到一个基准数,把它放在中间,左边都是比他小的,右边都是比他大的。然后再以此为分界线,左右两边依次照此规则递归即可。
具体如何将一个数放在中间,我们通常选取最左边的一个数作为基准数,主要思想就是两个哨兵,左侧哨兵从最左侧向右移动,找到比基准数大的数停止,右侧哨兵从最右侧向左移动,找到比基准数小的数停止,然后交换。直至左哨兵与右哨兵相遇,再将基准数同他们交换,即可完成。
程序实现:
public class Sort2 {
public void sort(int[] nums, int left, int right){
if(left<right){
int q = Partition(nums, left, right);
sort(nums, left, q-1);
sort(nums, q+1, right);
}
}
private int Partition(int[] nums, int left, int right){
int i = left+1;
int j = right;
int tmp;
while(true){
while (nums[j] > nums[left] && j != i) j-=1;
if(j==i) break;
while (nums[i] < nums[left] && j != i) i+=1;
if(j==i) break;
tmp = nums[j];
nums[j] = nums[i];
nums[i] = tmp;
}
tmp = nums[j];
nums[j] = nums[left];
nums[left] = tmp;
return i;
}
}参考资源:
坐在马桶上看算法:快速排序
三.简单选择排序
非常简单的排序算法,注意区分和冒泡的区别。
具体思想就是,拿第一个依次和后面的每一个比,遇到比他小的就换,一直比到头,第一个就是最小的了。然后再拿第二个依次和后面比,一直到头,小了就换。以此类推。
程序实现
/*简单选择排序*/
public class Sort3 {
public void sort(int[] nums){
for(int i = 0; i < nums.length; i++){
for(int j = i+1; j < nums.length; j++){
if(nums[i] > nums[j]){
int tmp = nums[j];
nums[j] = nums[i];
nums[i] = tmp;
}
}
}
}
}四.堆排序
关键词:不断构建大顶堆,挖走根元素
堆是一种重要的数据结构,为一棵完全二叉树。可以把一个数组看做一个堆。
堆分为大顶堆和小顶堆,大顶堆就是父节点比两个子节点大的堆,小顶堆反过来。堆排序的思想也很简单,升序排用大顶,降序排用小顶。每一次都把数组排成大顶堆,根节点就肯定是最大的了,把根节点和最后一个换一下,然后把除了最后一个的剩下的重新排成大顶堆,第二大的就是根节点了,以此类推。
综上,这个算法的核心就是如何把一个数组转换成大顶堆啦。直接看代码吧,
public class Sort4 {
public void sort(int[] nums){
if(nums == null || nums.length <= 1) return;
buildMaxHeap(nums, nums.length-1);
for(int i = nums.length-1; i >= 1; i--){
swap(nums,0, i);
buildMaxHeap(nums, i-1);
}
}
private void buildMaxHeap(int[] nums, int size){
if(nums == null || nums.length <= 1) return;
for(int i = size; i >= 0; i--){
maxHeap(nums, size, i);
}
}
private void maxHeap(int[] nums, int size, int index){
int left = 2*index + 1;
int right = 2*index + 2;
int largest = -1;
if(left <= size && nums[left] > nums[index]) largest = left;
if(right <= size && nums[right] > nums[index]) largest = right;
if(largest != -1){
if(left <= size && right <= size) largest=(nums[left]>nums[right])?left:right;
swap(nums, largest, index);
}
}
private void swap(int[] nums, int i, int j){
int tmp = nums[j];
nums[j] = nums[i];
nums[i] = tmp;
}
}程序的核心就是中间这两个函数。详细解答可以看参考资源:
堆排序(Heapsort)
五.直接插入排序
直接插入排序很简单,就是从第二个开始和它之前的比,从左往右将无序数组一点一点变成有序的。代码如下:
/*直接插入排序*/
public class Sort5 {
public void sort(int[] nums){
for(int i = 1; i < nums.length; i++){
for(int j = i-1; j >= 0; j--){
if(nums[j] > nums[j+1]) swap(nums, j, j+1);
else break;
}
}
}
private void swap(int[] nums, int i, int j){
int tmp = nums[j];
nums[j] = nums[i];
nums[i] = tmp;
}
}
参考资源:
插入排序详解
六.希尔排序
关键词:分组进行插入排序
希尔排序也是一种插入排序,它是简单插入排序经过改进之后的一个更高效的版本,也称为缩小增量排序。
简单来讲就是讲数组分组,对每个组里的元素进行插入排序。
我们选择增量gap=length/2,缩小增量继续以gap = gap/2的方式,这种增量选择我们可以用一个序列来表示,{n/2,(n/2)/2…1},称为增量序列。希尔排序的增量序列的选择与证明是个数学难题,我们选择的这个增量序列是比较常用的,也是希尔建议的增量,称为希尔增量,但其实这个增量序列不是最优的。此处我们做示例使用希尔增量。
代码:
/*
希尔排序(三个for循环)
*/
public class Sort6 {
public void sort(int[] nums){
for(int gap = nums.length/2; gap!=0; gap/=2){
for(int i = 0; i < gap; i++){
for(int j = i; j<nums.length; j+=gap){
if(j+gap < nums.length && nums[j] > nums[j+gap]) swap(nums, j, j+gap);
}
}
}
}
private void swap(int[] nums, int i, int j){
int tmp = nums[j];
nums[j] = nums[i];
nums[i] = tmp;
}
}
七.归并排序
关键词:递归,合并两个有序的数组
思路就是合并两个有序的数组,用递归,从最底层开始网上排即可。
代码:
/*
* 归并排序
* */
public class Sort7 {
private void mergeSortedArr(int[] arr, int start, int mid, int last){
int[] res = new int[last - start + 1];
int tmp;
int i = start, j=mid;
int k = 0;
while(i<mid && j <= last){
if(arr[i]<arr[j]) res[k++] = arr[i++];
else res[k++] = arr[j++];
}
while(i<mid){
res[k++] = arr[i++];
}
while(j<=last){
res[k++] = arr[j++];
}
for(i = 0; i<k; i++)
arr[start+i] = res[i];
}
public void sort(int[] nums, int start, int last){
if(start<last){
sort(nums, start, (start+last)/2);
sort(nums, (start+last)/2+1, last);
mergeSortedArr(nums, 0, nums.length/2, nums.length-1);
}
}参考资源:
归并排序
八.计数排序
排序原理:利用哈希的方法,将每个数据出现的次数都统计下来。哈希表是顺序的,所以我们统计完后直接遍历哈希表,将数据再重写回原数据空间就可以完成排序。
①因为要建立哈希表,计数排序只适用于对数据范围比较集中的数据集合进行排序。范围分散情况太浪费空间。如我有100个数,其中前99个都小于100,最后一个数位是10000,我们总不能开辟10000个数据大小的哈希表来进行排序吧!这样空间就太浪费了。 此时,就得考虑其他的算法了。当然,这个例子也可能不恰当,这里只是想让你们直观的理解。
②除了上面那种情况,还有一个问题,例如我有一千个数,1001~2000,此时我的哈希表该怎么开辟呢? 开0~2000个?那前面1000个空间就浪费了!直接从1001开始开辟?你想多了!所以这种情况我们就需要遍历一遍数据,找出最大值与最小值,求出数据范围。范围 = 最大值 - 最小值+1。 例如,2000-1001+1 = 1000,这样我们就开辟0~1000个空间,用1代表1001,1000代表2000。节省了大量的空间。
代码
/*计数排序*/
public class Sort8 {
public void sort(int[] nums){
int[] count = new int[11];
int k = 0;
for(int i:nums){
count[i]+=1;
}
for(int j=0; j<count.length; j++){
if(count[j] != 0){
for(int x = 0; x < count[j]; x++){
nums[k++] = j;
}
}
}
}
}
九.基数排序
基数排序是根据关键字中各位的值,通过对排序的N个元素进行若干趟“分配”与“收集”来实现排序的。
代码
/*
基数排序
*/
public class Sort9 {
public int getDigit(int x, int d) {
int a[] = {
1, 1, 10, 100
}; // 本实例中的最大数是百位数,所以只要到100就可以了
return ((x / a[d]) % 10);
}
public void radixSort(int[] list, int begin, int end, int digit) {
final int radix = 10; // 基数
int i = 0, j = 0;
int[] count = new int[radix]; // 存放各个桶的数据统计个数
int[] bucket = new int[end - begin + 1];
// 按照从低位到高位的顺序执行排序过程
for (int d = 1; d <= digit; d++) {
// 置空各个桶的数据统计
for (i = 0; i < radix; i++) {
count[i] = 0;
}
// 统计各个桶将要装入的数据个数
for (i = begin; i <= end; i++) {
j = getDigit(list[i], d);
count[j]++;
}
// count[i]表示第i个桶的右边界索引
for (i = 1; i < radix; i++) {
count[i] = count[i] + count[i - 1];
}
// 将数据依次装入桶中
// 这里要从右向左扫描,保证排序稳定性
for (i = end; i >= begin; i--) {
j = getDigit(list[i], d); // 求出关键码的第k位的数字, 例如:576的第3位是5
bucket[count[j] - 1] = list[i]; // 放入对应的桶中,count[j]-1是第j个桶的右边界索引
count[j]--; // 对应桶的装入数据索引减一
}
// 将已分配好的桶中数据再倒出来,此时已是对应当前位数有序的表
for (i = begin, j = 0; i <= end; i++, j++) {
list[i] = bucket[j];
}
}
}
public int[] sort(int[] list) {
radixSort(list, 0, list.length - 1, 3);
return list;
}
}
参考资源:
基数排序
十.桶排序
桶排序和基数排序贼像,只不过前者直接放数字,后者是放个数。
代码:
/*
* 桶排序
* */
public class Sort10 {
public void sort(int[] nums){
int[] count = new int[11];
int k = 0;
for(int i:nums) count[i]=i;
for(int j:count){
if(j!=0){
nums[k++] = j;
}
}
}
}
十一.总结
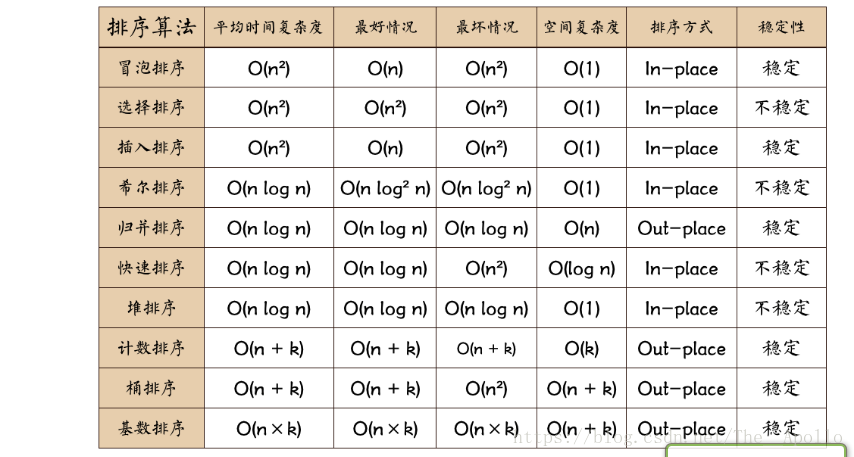
为了方便记忆,简单分以下类:
冒泡和快排属于交换类,一个easy,一个hard
直接插入和希尔排序属于插入类,一个easy,一个hard
简单选择和堆排属于选择类,一个easy一个hard
归并排序属于归并类,难度还行吧
基数排序,计数排序,桶排序属于非比较类,前两者easy,最后一个,代码实现hard,面试最好别写了吧,毕竟b装多了,容易扯着蛋
参考资源:
十种常见排序算法
基数排序与桶排序,计数排序【详解】







 这篇博客总结了十种经典的排序算法,包括冒泡排序、快速排序、选择排序、堆排序、插入排序、希尔排序、归并排序、计数排序、基数排序和桶排序。每种算法都阐述了其基本思想,并提供了Java代码实现。通过比较和分类,帮助读者理解和记忆各种排序算法的特点和适用场景。
这篇博客总结了十种经典的排序算法,包括冒泡排序、快速排序、选择排序、堆排序、插入排序、希尔排序、归并排序、计数排序、基数排序和桶排序。每种算法都阐述了其基本思想,并提供了Java代码实现。通过比较和分类,帮助读者理解和记忆各种排序算法的特点和适用场景。
















 1168
1168

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








