数据结构 之 排序算法

O(n^2)级别的排序算法

时间复杂度为O(n^2)的排序算法比较基础，但有重要的意义：
（1）编码简单，易于实现，是一些简单情景的首选
（2）在一些特殊的情况下，简单的排序算法更加有效
（3）简单的排序算法思想可以衍生出更加复杂的排序算法

选择排序

算法描述：每次从未排序的元素队列中，找到最小的那个元素并记录索引位置，再和未排序元素的队首进行交换，则蓝色有序部分长度相应加1

代码实现：

template<typename T>
void selectionSort(T arr[], int n){

    for(int i = 0 ; i < n ; i ++){

        int minIndex = i;
        for( int j = i + 1 ; j < n ; j ++ )
            if( arr[j] < arr[minIndex] )
                minIndex = j;

        swap( arr[i] , arr[minIndex] );
    }
}

插入排序

对于近乎有序的数组，插入排序能近乎得到最优的情况O(n)

算法描述：每次选择第一个未排序的元素，将其插入到蓝色有序部分中合适的位置；即该元素与每一个蓝色元素比较，若该元素小，则交换并继续向前比较判断，直至找到正确的位置

优化思路：每次判断比较时，不直接进行交换操作，而是先保存一份当前红色元素，然后当需要交换时，改为蓝色元素向后移动一格，最后将红色元素补入正确的位置中

template<typename T>
void insertionSort(T arr[], int n){

    for( int i = 1 ; i < n ; i ++ ) {

        // 寻找元素arr[i]合适的插入位置
        T e = arr[i];
        int j; 	// j保存元素e应该插入的位置
        for (j = i; j > 0 && arr[j-1] > e; j--)
            arr[j] = arr[j-1];
        arr[j] = e;
    }

    return;
}

冒泡排序

算法描述：每次循环中，对于未排序的元素序列，依次向后两两比较，若前者大于后者则进行交换，最终将本轮最大的元素放入序列尾部，则已经排序的序列（数组尾部）长度加1

O(nlogn)级别的排序算法

归并排序

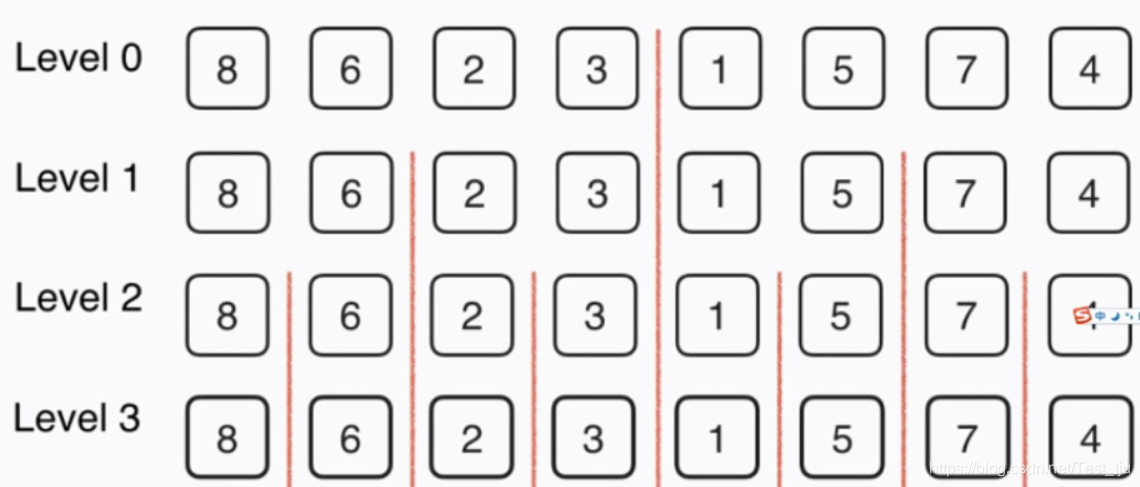
算法描述：先拆分，将数组对半拆分，直至成为最小单位；再归并，每两个被对半拆分的单位向上归并，使得合并后的子序列是有序的

template<typename T>	// 分组
void __mergeSort(T arr[], int l, int r){

    if( r - l <= 15 ){
        insertionSort(arr, l, r);
        return;
    }

    int mid = (l+r)/2;
    __mergeSort(arr, l, mid);
    __mergeSort(arr, mid+1, r);
    if( arr[mid] > arr[mid+1] )
        __merge(arr, l, mid, r);
}

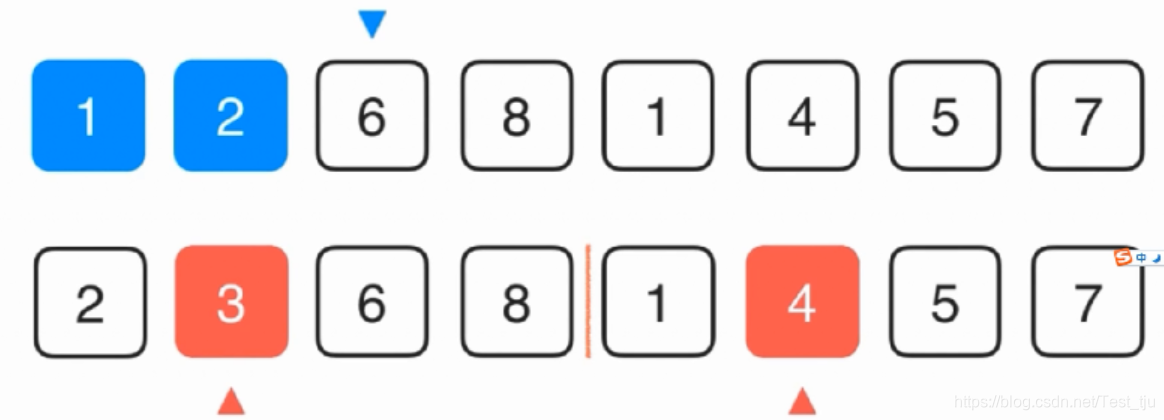
归并过程：将两个有序的子数组复制一份，标记为左和右；然后从左、右数组中各取第一个未使用的元素进行比较，小的放入合并后的大数组中，下次比较则选取其后面的一个元素；直至所有元素都放入大数组

代码实现：

template<typename  T>	// 归并
void __merge(T arr[], int l, int mid, int r){
	// 复制元素
    T aux[r-l+1];
    for( int i = l ; i <= r; i ++ )
        aux[i-l] = arr[i];
        
	// 将两个子数组的元素有序放入归并后的数组
    int i = l, j = mid+1;	
    for( int k = l ; k <= r; k ++ ){
        if( i > mid )   { arr[k] = aux[j-l]; j ++;}
        else if( j > r ){ arr[k] = aux[i-l]; i ++;}
        else if( aux[i-l] < aux[j-l] ){ arr[k] = aux[i-l]; i ++;}
        else                          { arr[k] = aux[j-l]; j ++;}
    }
}

优化思路：当元素量较小时，归并排序效率不一定优于插入排序，因此对于递归到底的情况，可以选择两种排序算法的混合使用

 if( r - l <= 15 ){
        insertionSort(arr, l, r);
        return;
 }

自底向上的归并排序：思路与递归的归并排序类似，对于一个无序的数组，每次循环中，选择两个最小单位的有序子序列进行归并操作

template <typename T>
void mergeSortBU(T arr[], int n){

//    for( int sz = 1; sz <= n ; sz += sz )
//        for( int i = 0 ; i < n ; i += sz+sz )
//            // 对 arr[i...i+sz-1] 和 arr[i+sz...i+2*sz-1] 进行归并
//            __merge(arr, i, i+sz-1, min(i+sz+sz-1,n-1) );

    // Merge Sort Bottom Up 优化
    for( int i = 0 ; i < n ; i += 16 )
        insertionSort(arr,i,min(i+15,n-1));

    for( int sz = 16; sz <= n ; sz += sz )
        for( int i = 0 ; i < n - sz ; i += sz+sz )
            if( arr[i+sz-1] > arr[i+sz] )
                __merge(arr, i, i+sz-1, min(i+sz+sz-1,n-1) );
}

比较：两种归并排序效率差不多，但是自底向上没有使用数组索引获取元素，可以用于对链表结构进行nlogn排序

快速排序

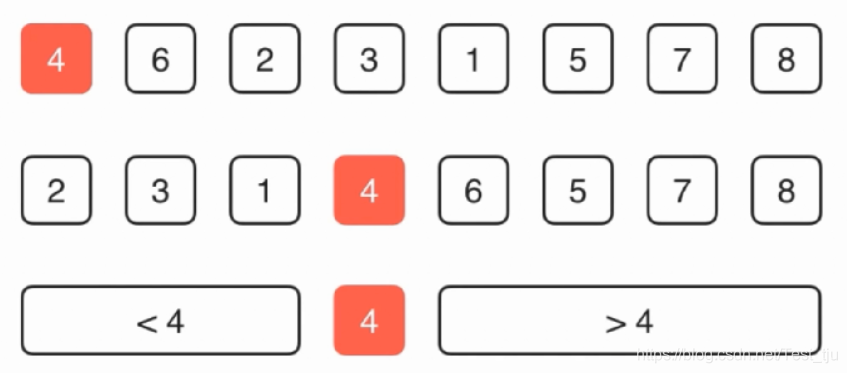
算法描述：随机选定数组中的一个元素，将其放置到合适的位置（Partition过程），保证其之前的元素都比它小，其之后的元素都比它大；之后再对前后两个部分分别使用快速排序

代码实现：

template <typename T>
void _quickSort(T arr[], int l, int r){

    if( r - l <= 15 ){
        insertionSort(arr,l,r);
        return;
    }

    int p = _partition(arr, l, r);
    _quickSort(arr, l, p-1 );
    _quickSort(arr, p+1, r);
}

Partition过程：红色部分元素v为目标元素，蓝色部分e为当前比较的元素。若e>v，则e直接并入紫色部分；若e<v，则e和紫色部分队首arr[j+1]交换，同时j++；最后，将v放置到合适的位置，即与橙色部分队尾arr[j]交换

优化思路1：当需要排序的数组足够小时，直接使用插入排序完成

优化思路2：随机选取目标元素v，使一次Partition后前后两部分大小差距相对平均，避免在有序数组情况下退化为O(n^2)

 swap( arr[l] , arr[rand()%(r-l+1)+l] );
 T v = arr[l];

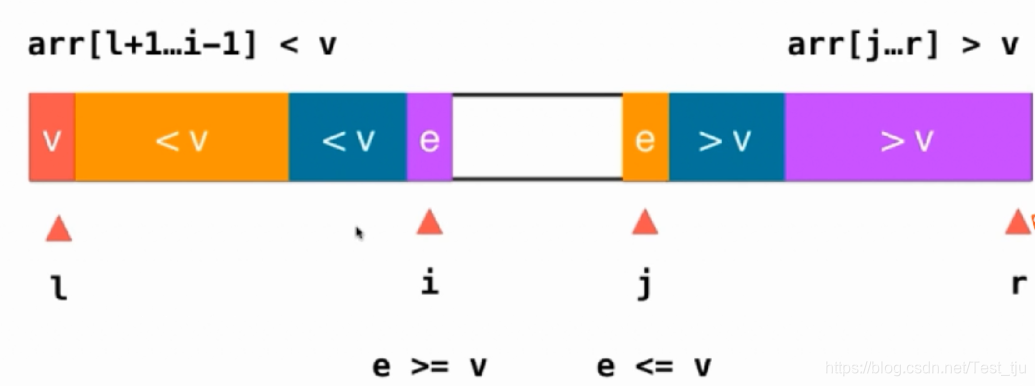
优化思路3：避免等于v的元素全部集中在一个部分引起退化，将其均匀地分散在前后两部分中。如图，从前向后判断直至e>=v，从后向前判断直至e<=v，然后进行一次交换；继续重复操作；最后将红色元素v和前一部分的队尾交换

代码实现：

template <typename T>
int _partition(T arr[], int l, int r){

    swap( arr[l] , arr[rand()%(r-l+1)+l] );
    T v = arr[l];

    // arr[l+1...i) <= v; arr(j...r] >= v
    int i = l+1, j = r;
    while( true ){
        while( i <= r && arr[i] < v )
            i ++;

        while( j >= l+1 && arr[j] > v )
            j --;

        if( i > j )
            break;

        swap( arr[i] , arr[j] );
        i ++;
        j --;
    }

    swap( arr[l] , arr[j]);

    return j;
}

优化思路4（三路快排）：在思路3的基础上，将等于元素v的元素集体保存

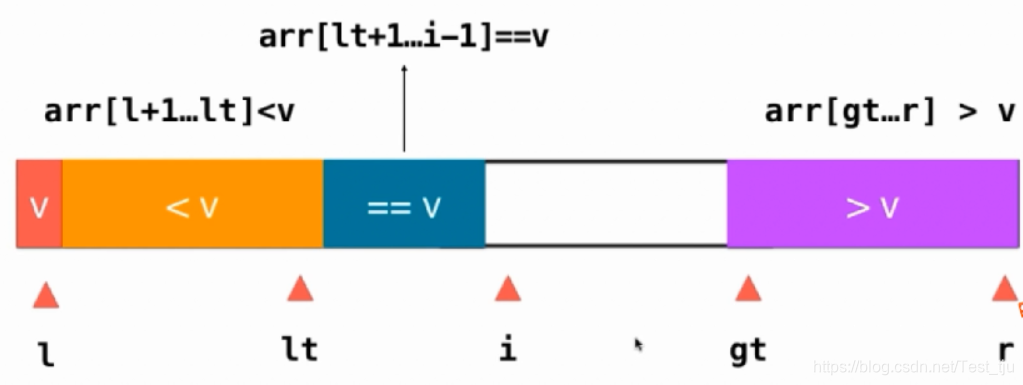
代码实现：

template <typename T>
void __quickSort3Ways(T arr[], int l, int r){

    if( r - l <= 15 ){
        insertionSort(arr,l,r);
        return;
    }

    swap( arr[l], arr[rand()%(r-l+1)+l ] );

    T v = arr[l];

    int lt = l;     // arr[l+1...lt] < v
    int gt = r + 1; // arr[gt...r] > v
    int i = l+1;    // arr[lt+1...i) == v
    while( i < gt ){
        if( arr[i] < v ){
            swap( arr[i], arr[lt+1]);
            i ++;
            lt ++;
        }
        else if( arr[i] > v ){
            swap( arr[i], arr[gt-1]);
            gt --;
        }
        else{ // arr[i] == v
            i ++;
        }
    }

    swap( arr[l] , arr[lt] );

    __quickSort3Ways(arr, l, lt-1);
    __quickSort3Ways(arr, gt, r);
}

总结：归并排序、快速排序都使用了分治算法，归并排序主要处理合并过程，快速排序主要处理分类过程