经纬度转高斯投影坐标（xy平面坐标）

最新推荐文章于 2025-07-21 11:04:49 发布

转载最新推荐文章于 2025-07-21 11:04:49 发布 · 8.7k 阅读

87 ·

CC 4.0 BY-SA版权

原文链接：https://blog.youkuaiyun.com/weixin_44088559/article/details/104014363

文章标签：

#高斯投影 #C++ #经纬度 #xy坐标

该博客详细介绍了高斯投影的正解和反解算法，包括3度带和6度带的计算，涉及经纬度与平面直角坐标的转换。算法适用于WGS84坐标系，可用于地理信息系统和测绘领域的坐标转换。

参考链接

https://blog.youkuaiyun.com/weixin_44088559/article/details/104014363

计算模型

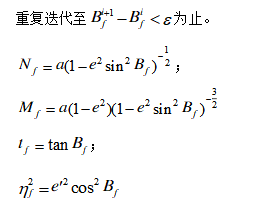
在这里插入图片描述

高斯投影正解

int LongLat2XY(double longitude,double latitude,double &X,double &Y)
{
    int ProjNo=0; int ZoneWide; //带宽
    double longitude1,latitude1, longitude0,latitude0, X0,Y0, xval,yval;
    double a, f, e2, ee, NN, T, C, A, M, iPI;
    iPI = 0.0174532925199433;  //3.1415926535898/180.0;
    ZoneWide = 3;  //3度带宽
    //ZoneWide = 6; 6度带宽
    //a=6378245.0; f=1.0/298.3; //54年北京坐标系参数
    //a=6378140.0; f=1/298.257; //80年西安坐标系参数
    a = 6378137.0; f = 1.0/298.257223563;//WGS84坐标系参数
    //ProjNo = (int)(longitude / ZoneWide) ;      //6度带
    //longitude0 = ProjNo * ZoneWide + ZoneWide / 2; //6度带
    ProjNo = (int)(longitude / ZoneWide+0.5) ;
    // ProjNo = (int)(longitude / ZoneWide) ; //--带号
    longitude0 = ProjNo * ZoneWide ; //--中央子午线
    longitude0 = longitude0 * iPI ;//--中央子午线转化为弧度
    latitude0=0;
    longitude1 = longitude * iPI ; //经度转换为弧度
    latitude1 = latitude * iPI ; //纬度转换为弧度
    e2=2*f-f*f;
    ee=e2*(1.0-e2);
    NN=a/sqrt(1.0-e2*sin(latitude1)*sin(latitude1));
    T=tan(latitude1)*tan(latitude1);
    C=ee*cos(latitude1)*cos(latitude1);
    A=(longitude1-longitude0)*cos(latitude1);

    M=a*((1-e2/4-3*e2*e2/64-5*e2*e2*e2/256)*latitude1-(3*e2/8+3*e2*e2/32+45*e2*e2*e2/1024)*sin(2*latitude1)
         +(15*e2*e2/256+45*e2*e2*e2/1024)*sin(4*latitude1)-(35*e2*e2*e2/3072)*sin(6*latitude1));
    xval = NN*(A+(1-T+C)*A*A*A/6+(5-18*T+T*T+72*C-58*ee)*A*A*A*A*A/120);
    yval = M+NN*tan(latitude1)*(A*A/2+(5-T+9*C+4*C*C)*A*A*A*A/24
                                +(61-58*T+T*T+600*C-330*ee)*A*A*A*A*A*A/720);
    //X0 = 1000000L*(ProjNo+1)+500000L; //6度带
    X0 = 1000000L*ProjNo+500000L;  //3度带
    Y0 = 0;
    xval = xval+X0; yval = yval+Y0;

    X= xval;
    Y= yval;
    //printf("%lf   %lf\r\n",xval,yval);
    return 1;
}

高斯投影反解

int XY2LongLat(double X,double Y,double& longitude,double& latitude)
{
    int ProjNo; int ZoneWide; //带宽
    double longitude1,latitude1, longitude0,latitude0, X0,Y0, xval,yval;
    double e1,e2,f,a, ee, NN, T,C, M, D,R,u,fai, iPI;
    iPI = 0.0174532925199433;  //3.1415926535898/180.0;
    ///a = 6378245.0; f = 1.0/298.3; //54年北京坐标系参数 f:扁率
    //a=6378140.0; f=1/298.257; //80年西安坐标系参数
    a = 6378137.0; f = 1.0/298.257223563;//WGS84坐标系参数
    ProjNo = (int)(X/1000000L) ; //查找带号
    // 	ZoneWide = 6; 6度带宽
    // 	longitude0 = (ProjNo-1) * ZoneWide + ZoneWide / 2; //计算每带中央子午线经度
    ZoneWide=3;   //3度带宽
    longitude0 =  ProjNo * ZoneWide;
    longitude0 = longitude0 * iPI ; //中央经线

    X0 = ProjNo*1000000L+500000L;
    Y0 = 0;
    xval = X-X0; yval = Y-Y0; //带内大地坐标
    e2 = 2*f-f*f;
    e1 = (1.0-sqrt(1-e2))/(1.0+sqrt(1-e2));
    ee = e2/(1-e2);
    M = yval;
    u = M/(a*(1-e2/4-3*e2*e2/64-5*e2*e2*e2/256));
    fai = u+(3*e1/2-27*e1*e1*e1/32)*sin(2*u)+(21*e1*e1/16-55*e1*e1*e1*e1/32)*sin(4*u)
          +(151*e1*e1*e1/96)*sin(6*u)+(1097*e1*e1*e1*e1/512)*sin(8*u);
    C = ee*cos(fai)*cos(fai);
    T = tan(fai)*tan(fai);
    NN = a/sqrt(1.0-e2*sin(fai)*sin(fai));// 字串1
    R = a*(1-e2)/sqrt((1-e2*sin(fai)*sin(fai))*(1-e2*sin(fai)*sin(fai))*(1-e2*sin(fai)*sin(fai)));
    D = xval/NN;
    //计算经度(Longitude) 纬度(Latitude)
    longitude1 = longitude0+(D-(1+2*T+C)*D*D*D/6+(5-2*C+28*T-3*C*C+8*ee+24*T*T)*D*D*D*D*D/120)/cos(fai);
    latitude1 = fai -(NN*tan(fai)/R)*(D*D/2-(5+3*T+10*C-4*C*C-9*ee)*D*D*D*D/24+(61+90*T+298*C+45*T*T-256*ee-3*C*C)*D*D*D*D*D*D/720);
    int g=0;
    //转换为度 DD
    longitude = longitude1 / iPI;
    latitude = latitude1 / iPI;

    return 1;
}