西瓜书（机器学习_周志华）课后题答案

我自己瞎做的、多多交流

 答案：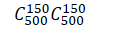

 

 答案：

采用10折交叉验证，因为取样是随机的，所以获得的结果是50%

如果采用留一法，不管最后留下来是正例还是反例，都会和预测结果不一致，（如果留下正例，预测集中反例占多数，预测结果为反例，反之亦然），所以对错误率进行评估的结果是100%

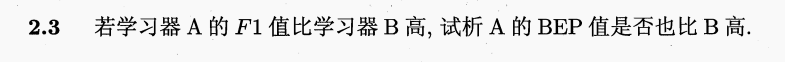
 答案：

 

 答案：

真正例率：正例中被预测为正例的比例   TP/(TP+FN)

假正例率：假例中被预测为正例的比例  EP/(EP+TN)

查全率(R/召回率)：TP/(TP+FN) 也是正例中被预测为正例的比例

查准率（P/）：TP/(TP+FP)  正例占所有被预测为正例的比例

真正例率在数值上等于查全率

`百度百科：`查全率与查准率为互逆相关性,查全率一般为60%～70%,查准率约为40%～50%,当查全率超过70%时,若想再提高查全率就必然降低查准率。

先不写了，改天有时间再接着写