【学习笔记】CH5 Binary Trees | Data Structure& Algorithm Analysis in C++（ed. 3)

Definitions and Properties

Nodes, subtrees.
Ancestors and descendants 后代和前面点的关系
Parent and child. 直接的上下关系
Depth of the node M: the length of the path from the root to M
Height: depth of the deepest node +1
The level of the node: node of depth d is of levels. The root is at level 0
Full binary tree: where a node is either an internal node with two non-empty children or a leaf.
Complete binary tree: start at the root and fill the tree from left to right; all the levels except the d-1 level are full.

• Full binary tree theorem:
  In a full non-empty binary tree, the number of leaf nodes is one more than internal nodes.
  The number of empty subtrees in a non-empty binary tree is one more than the number of nodes in the tree.

The binary tree ADT: class BinNode. The functions will either set and return the element, pointers and also whether this node is a leaf.

// Binary tree ADT
template<typename E> class BinNode{
   
public:
	virtual ~BinNode(){
   }//base destructor
	virtual E& element() = 0;//get the node’s value
	virtual void setElement(const E& ) = 0;// set the node’s element value
	virtual BinNode* left() const = 0; //get the left child of the node
	virtual BinNode* right() const = 0; // get the right child of the node
	virtual void setLeft(BinNode*) = 0; // set the left child
	virtual void setRight(BinNode*) = 0; //set the right child
	virtual bool isLeaf() = 0; //return whether this node is a leaf	
}

Binary Tree Traversals

Visiting the nodes: traversal; enumeration: a traversal that lists every node in the tree once.

preorder traversal:

Visit any given nodes before visiting its children. Visit the left children and then the right children.
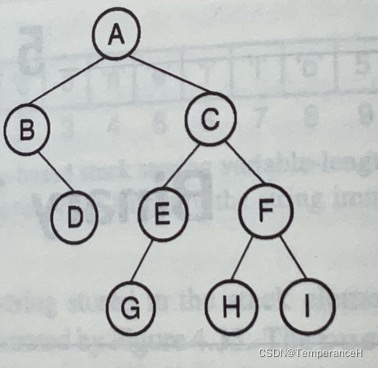
Therefore, the order of visit would be: ABDCEGFHI. Parent first, then the left children, then the right children.

- Implementation of preorder traversal:(the other implementation is not so efficient therefore we don’t show it.)

template <typename E>
void preorder(BinNode<E>* root){
   //we set the root of the tree as entrance
	if (root == NULL) return;
	visit(root); //do something
	preorder(root->left);
	preorder(root->right);//first left then right
}

postorder traversal:

Visit the child of any internal nodes first. We start with a leaf, we judge whether its parent has another child, if not, visit the parent, if yes, visit the other child.
Therefore the order of visit would be DBGEHIFCA. We judge every time whether this node has a parent.
This traversal is useful when deleting nodes, when we delete the children before the parents.

- Implementation of postorder, similar as preorder

template <typename E>
void postorder(BinNode<E>* root){
   
	if (root==NULL) return;
	postorder(root->left);
	postorder(root->right);//first the left children, then right children, then the parent
	visit(root);//do something
}

In order traversal:

Visit the left child, then the parent node, then the right part the tree.
Therefore the order of visit would be BDAGECHFI.

- Implementation of inorder traversal, similar to preorder traversal

template<typename E>
void inorder(BinNode<E>* root){
   
	if (root==NULL) return;
	inorder(root->left);
	visit(root);//do something
	inorder(root->right);//first the left children, then right children, then the parent
}

A recursive count of node implementation

template <typename E>
int count(BinNode<E>* root<