基于线性回归的房价预测分析

一、分析问题

         尝试使用线性回归模型分析波士顿房价数据集，达到可通过房子属性（X）预测房价（y）的效果。

二、获取数据

sklearn.datasets中自带的load_boston数据集。

三、数据探索

1、数据探索

#导入所有可能需要用到的python包
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
#导入数据
from sklearn.datasets import load_boston
d=load_boston()
d#查看数据集

得出load_boston是一个字典，包含“data”、“target”、“feature_names”、“DESCR”四个key。

其中data表示房屋特征，target表示房价，各特征解释如下：

CRIM  ------【城镇人均犯罪率】
ZN -------【住宅用地所占比例】
INDUS   ------【城镇中非商业用地占比例】
CHAS  ------【查尔斯河虚拟变量，如果是河道，则为1;否则为0 ）】
NOX   ------【环保指标】
RM -------【每栋住宅房间数】
AGE------【1940年以前建造的自住单位比例 】
DIS ------【与波士顿的五个就业中心加权距离】
RAD ------【距离高速公路的便利指数】
TAX  ------【每一万美元的不动产税率】
PTRATIO  ------【城镇中教师学生比例】
B ------【城镇中黑人比例】
LSTAT ------【房东属于低等收入阶层比例】
MEDV  ------【自住房屋房价中位数】

以‘data’为X，‘target’为y，对数据进行探索。

X=d['data']
y=d['target']
X.shape

X为506行，14列的数组，即共有14个特征。

四、构建模型

1、简单线性回归

（1） 预测、拟合、画图展示

#使用sklearn简单线性回归的库
from sklearn.linear_model import LinearRegression

#实例化一个简单线性回归
clf = LinearRegression()
#需要根据已知的x和y进行训练
clf.fit(X,y)

#使用上述模型预测y
y_pred=clf.predict(X)

x = list(range(len(y)))
plt.plot(x,y,label = 'true')#实际的y
plt.plot(x,y_pred,label = 'pred')#预测的y
plt.legend()#展示下图例
plt.show()

 

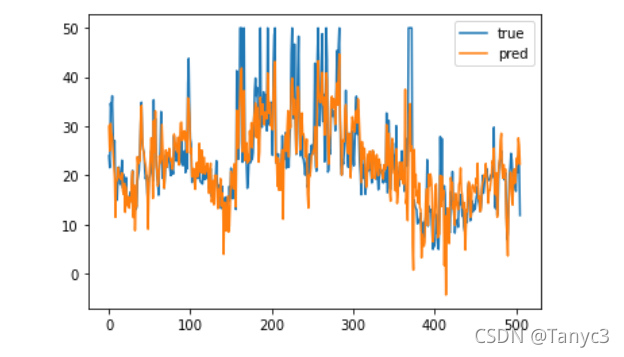
（2）模型检验

以MSE作为该模型的评价标准

from sklearn.metrics import mean_squared_error

mean_squared_error(y,y_pred)

求得MSE为21.894831181729206。

（3）模型上线

求出该简单线性回归模型的的各特征系数：

clf.coef_

array([-1.08011358e-01,  4.64204584e-02,  2.05586264e-02,  2.68673382e+00,
       -1.77666112e+01,  3.80986521e+00,  6.92224640e-04, -1.47556685e+00,
        3.06049479e-01, -1.23345939e-02, -9.52747232e-01,  9.31168327e-03,
       -5.24758378e-01])

2、岭回归

（1）划分训练集与测试集

以5:1的比例划分训练集与测试集

#划分训练集和测试集
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size = 0.2)

（2）模型拟合

对训练集和测试集分别进行岭回归模型拟合

#导入岭回归模型
from sklearn.linear_model import Ridge

#实例化一个简单线性回归
clf1 = Ridge()

#代入训练集进行拟合
clf1.fit(X_train,y_train)

Ridge(alpha=1.0, copy_X=True, fit_intercept=True, max_iter=None,
   normalize=False, random_state=None, solver='auto', tol=0.001)

（3）模型预测

#进行预测
y_train_pred = clf.predict(X_train)
y_test_pred = clf.predict(X_test)

 （4）模型检验

使用MSE作为评价标准，分别计算训练集和测试集的MSE：

from sklearn.metrics import mean_squared_error
#训练集
mean_squared_error(y_train_pred,y_train)

#测试集
mean_squared_error(y_test_pred,y_test)

得到训练集的MSE为21.208910759864875，测试集的MSE为26.238961891823568，存在一定过拟合问题。

（5）模型调参

       相较于简单线性回归，岭回归在模型中多了一个正则化项，通过控制这一常数项，调整误差的大小、调整欠拟合、过拟合问题。

为探索最佳alpha，取多个值进行对比

alphas=[0.001,0.005,0.1,0.2,0.3,0.4,0.5,1,2]
mse_train=[]
mse_test=[]
for alpha in alphas:
    clf1=Ridge(alpha=alpha)
    clf1.fit(X_train,y_train)
    y_train_pred=clf1.pred(X_train)
    y_test_pred=clf1.pred(X_test)
    mse_train.append(mean_squared_error(y_train_pred,y_train)
    mse_test.append(mean_squared_error(y_test_pred,y_test)

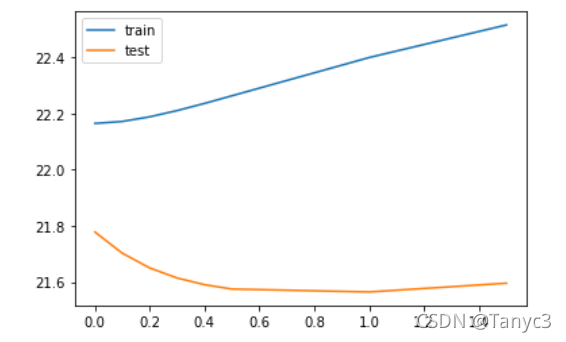
绘制alpha与MSE的趋势图

plt.plot(alpha,mse_trains,label='train')
plt.plot(alpha,mse_test,label='test')

 由上图可见alpha=0.4较为合适。

（6）模型上线

调整alpha的值，重新拟合、预测：

#实例化一个简单线性回归
clf2 = Ridge(alpha=0.4)

#代入训练集进行拟合
clf2.fit(X_train,y_train)

#进行预测
y_train_pred = clf2.predict(X_train)
y_test_pred = clf2.predict(X_test)

并求出此时岭回归模型的的各特征系数：

clf2.coef_

array([-8.47432333e-02,  4.54381359e-02, -1.37582594e-03,  1.62425395e+00,
       -1.02516535e+01,  3.94872014e+00,  4.57532581e-03, -1.21689112e+00,
        3.03010923e-01, -1.32502735e-02, -9.18887516e-01,  9.18609075e-03,
       -5.65646796e-01])

至此，模型建立完毕。