HDU - 1796——容斥原理+二进制枚举

【题目描述】
Now you get a number N, and a M-integers set, you should find out how many integers which are small than N, that they can divided exactly by any integers in the set. For example, N=12, and M-integer set is {2,3}, so there is another set {2,3,4,6,8,9,10}, all the integers of the set can be divided exactly by 2 or 3. As a result, you just output the number 7.
Input
There are a lot of cases. For each case, the first line contains two integers N and M. The follow line contains the M integers, and all of them are different from each other. 0<N<2^31,0<M<=10, and the M integer are non-negative and won’t exceed 20.
Output
For each case, output the number.
Sample Input

12 2
2 3

Sample Output

7

【题目分析】
首先我们需要学习一下容斥原理，不懂的话可以移步去看一下这篇大佬的博客：传送门
里面讲的很详细，除去证明之类的，我觉得比较重要的是容斥原理的公式

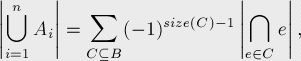
emm，看起来可能不太像人话，翻译一下就是几个集合的并集的元素的个数等于每个集合的个数减去集合两两相交的集合的元素的个数加上集合三三相交的集合的元素的个数……
然后我们就能解决这个问题啦，因为想求的是$(0,n)$内能被集合内元素整除的数的个数，我们把每个元素整除的数看作一个集合，那么我们想求的就是这些集合并集的元素的个数。而每个元素的个数挺好求的，就是(n-1)/元素的最小公倍数。
然后我们进行枚举就可以啦，只是直接枚举的话得需要用dfs稍微有些麻烦，我们用二进制枚举进行优化。
$PS:$题目说的是非负数，所以说有可能含0，注意读入的时候将0滤去。而且数字最大为n-1，取不到n

【AC代码】

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<iostream>
#include<cmath>
#include<climits>
#include<queue>
#include<vector>
#include<set>
#include<map>
using namespace std;

typedef long long ll;
const int MAXN=15;
int a[MAXN];
int n,m,r;
int ans,sign,t;

int gcd(int a,int b)
{
    return a%b==0?b:gcd(b,a%b);
}

int main()
{
    while(~scanf("%d%d",&n,&m))
    {
        r=n-1;
        ans=0;
        int h=0;
        for(int i=0;i<m;i++)
        {
            scanf("%d",&a[h]);
            if(a[h]) h++;
        }
        m=h;
        for(int i=1,limit=1<<m;i<limit;i++)
        {
            sign=0; t=1;
            for(int j=0;j<m;j++)
            {
                if(i&(1<<j))
                {
                    sign++;
                    t=a[j]/gcd(a[j],t)*t;
                }
            }
            if(sign%2)
            {
                ans+=r/t;
            }
            else
            {
                ans-=r/t;
            }
        }
        printf("%d\n",ans);
    }

    return 0;
}