BZOJ2115XOR——线性基

最新推荐文章于 2021-07-16 19:48:55 发布

王江奎

最新推荐文章于 2021-07-16 19:48:55 发布

阅读量268

点赞数

CC 4.0 BY-SA版权

本文链接：https://blog.youkuaiyun.com/T_T233333333/article/details/98589635

本文深入解析BZOJ2115 XOR问题，介绍如何利用线性基理论解决复杂的路径和环形结构问题。文章强调了重复路径的抵消原理，并提出了一种有效的算法策略，即通过选取特定路径并结合各环构造线性基来求解最大值。同时，分享了一个实用的线性基板子，展示了面向板子编程的高效性和乐趣。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

【题目描述】
BZOJ2115XOR——线性基
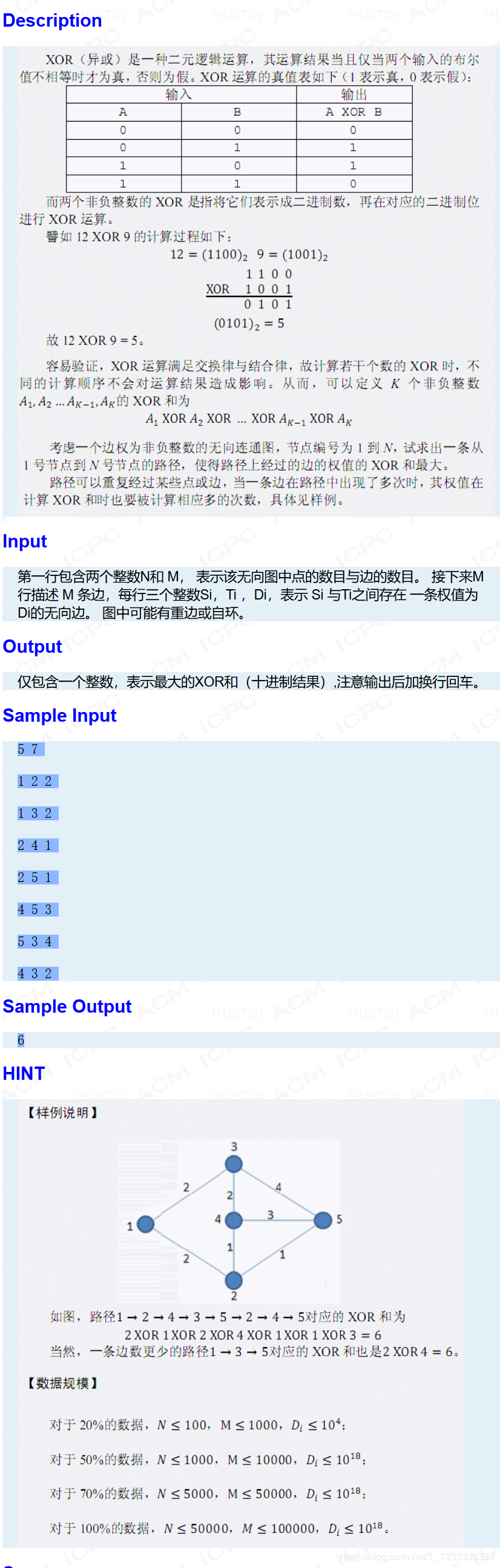
在这里插入图片描述
【题目分析】
这道题看完以后很懵逼，人家要是走的很复杂呢？各种绕来绕去怎么办？
首先我们应该注意到一个很明显的道理：重复的路径会和自身抵消，所以我们大可以随便跑，只要再跑回来就对答案没有影响。因此，有影响的只有选择的路径和经过的环，因为环是可以回到已经经过的点而不抵消的。而且只要我们愿意我们可以去任何一个环（假如环有一个起点x，我们有一条从1到n的路径，可能这个环和路径没有交点，但是我们可以从某一点跑到x然后经过这个环再跑回来，这样我们就经过这个环了）
我们算法的策略是：任选一个从1到n路径的xor和作为初始值然后再以各个环作为线性基求最大值
可能你会疑惑，任意选一个路径真的没有问题吗？假如从1到n只有这一条路径我们显然必须选，可是有很多路径的时候他们就会构成环，而我们已经将各种环都加入线性基了，通过选的这条路和其他环的异或我们就能得到其他路径（相当于可以被抵消）
另外，面向板子编程真的好爽，以后一定要认认真真的整理板子。这个线性基的板子就挺好用
【参考博客】
BZOJ2115 [Wc2011] Xor
【AC代码】

#include<cstdio>
#include<cstring>
#include<cmath>
#include<climits>
#include<cstdlib>
#include<algorithm>
#include<queue>
#include<vector>
#include<set>

using namespace std;

typedef long long ll;

const int MAXN=50005;
const int MAXM=100005;
struct node
{
	int from,to;
	ll weight;
}edge[MAXM<<1];
int head[MAXM<<1],nxt[MAXM<<1];
int tot=0;
int n,m;
ll dis[MAXN];
bool vis[MAXN];

struct L_B
{
	ll b[65],p[65];
	int cnt,flag;
	L_B()
	{
		memset(p,0,sizeof(p));
		memset(b,0,sizeof(b));
		cnt=flag=0;
	}
	inline bool insert(ll x)
	{
		for(int i=62;i>=0;--i)
			if(x&(1ll<<i))
			{
				if(b[i])
					x^=b[i];
				else
				{
					b[i]=x;
					return true;
				}
			}
		flag=1;
		return false;
	}
	ll get_max()
	{
		ll ret = 0;
		for(int i=62;i>=0;--i)
			if((ret^b[i])>ret)
				ret^=b[i];
		return ret;
	}
	ll get_max(ll initval)
	{
		ll ret = initval;
		for(int i=62;i>=0;--i)
			if((ret^b[i])>ret)
				ret^=b[i];
		return ret;
	}
	ll get_min()
	{
		if(flag)
			return 0;
		for(int i=0;i<=62;++i)
			if(b[i])
				return b[i];
		return 0;
	}
	inline void rebuild()
	{
		for(int i = 1;i <= 62;++i)
			if(b[i])
				for(int j=0;j<i;++j)
					if(b[i]&(1ll<<j))
						b[i]^=b[j];
		for(int i=0;i<=62;++i)
			if(b[i])
				p[cnt++]=b[i];
	}
	ll kth(ll k)
	{
		if(flag)
			--k;
		if(k==0)
			return 0;
		ll ret = 0;
		if(k>=(1ll<<cnt))
			return -1;
		for(int i=0;i<=cnt-1;++i)
			if(k&(1ll<<i))
				ret^=p[i];
		return ret;
	}
};
L_B lis;

inline int getint(){int w=0,q=0;char c=getchar();while((c<'0'||c>'9')&&c!='-')c=getchar();if(c=='-')q=1,c=getchar();while (c>='0' && c<='9') w=w*10+c-'0', c=getchar(); return q ? -w : w;}
inline ll getlong(){ll w=0,q=0;char c=getchar();while((c<'0' || c>'9')&&c!='-')c=getchar();if(c=='-') q=1,c=getchar();while (c>='0' && c<='9') w=w*10+c-'0', c=getchar(); return q ? -w : w;}

void AddEdge(int u,int v,ll w)
{
	tot++;
	edge[tot].from=u; edge[tot].to=v; edge[tot].weight=w;
	nxt[tot]=head[u]; head[u]=tot;
}

void dfs(int x)
{
	int v;
	vis[x]=true;
	for(int i=head[x];i;i=nxt[i])
	{
		v=edge[i].to;
		if(!vis[v])
		{
			dis[v]=dis[x]^edge[i].weight;
			dfs(v);
		}
		else
		{
			lis.insert(dis[x]^dis[v]^edge[i].weight);
		}
	}
}

int main()
{
	int u,v; ll w;
	n=getint(); m=getint();
	for(int i=0;i<m;i++)
	{
		u=getint(); v=getint(); w=getlong(); 
		AddEdge(u,v,w); AddEdge(v,u,w);
	}
	dfs(1);
	printf("%lld",lis.get_max(dis[n]));
	return 0;
}