K- means 聚类算法简单解释(记一次课程presentation）

#什么是算法

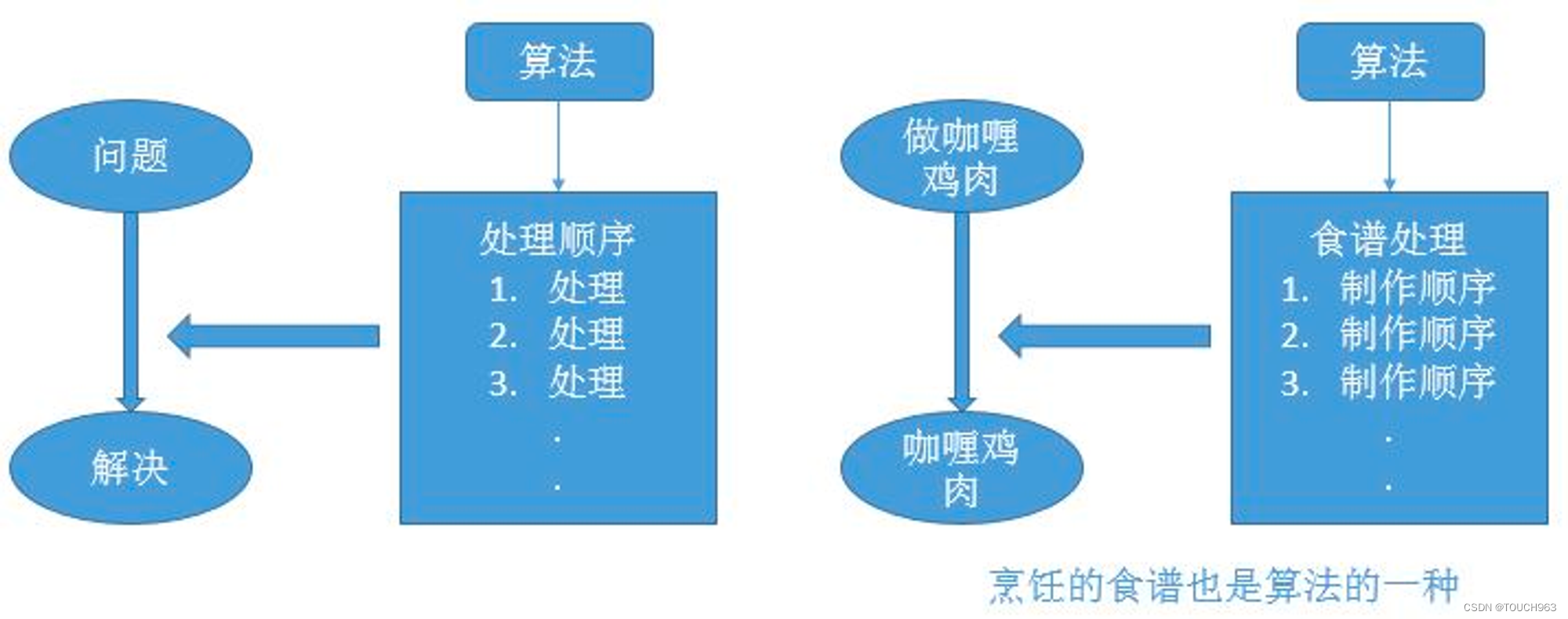
• 字面意义：算法就是解决问题的步骤。

• 专业定义：算法是模型分析的一组可行的，确定的，有穷的规则。

  通俗的说，算法也可以理解为一个解题步骤，有一些基本运算和规定的顺序构成。但是从计算机程序设计的角度看，算法由一系列求解问题的指令构成，能根据规范的输入，在有限的时间内获得有效的输出结果。算法代表了用系统的方法来描述解决问题的一种策略机制。

• 算法可以类比为烹饪中用到的食谱。

• 

   

  #k-means算法简介

• 历史

  • 最早是由MacQueen J. 在论文Classification and analysis of multivariate observations

    Math. Statist. Probability. Los Angeles LA USA: University of California, 1967: 281-297.

    MacQueen J. Symp. Math. Statist. Probability. 1967: 281-297.

  • James MacQueen 于 1967 年首次使用术语“ k均值”， [2]尽管该想法可追溯到1956 年的Hugo Steinhaus。[3]标准算法于 1957 年由贝尔实验室的 Stuart Lloyd 首次提出，作为一种技术用于脉冲编码调制，尽管它直到 1982 年才作为期刊文章发表。[4] 1965 年，Edward W. Forgy 发表了基本上相同的方法，这就是为什么它有时被称为 Lloyd-Forgy 算法。

• 快速理解

  1.有四个牧师去郊区布道，一开始牧师们随意选了几个布道点，并且把这几个布道点的情况公告给了郊区所有的居民，于是每个居民到离自己家最近的布道点去听课。

  2.听课之后，大家觉得距离太远了，于是每个牧师统计了一下自己的课上所有的居民的地址，搬到了所有地址的中心地带，并且在海报上更新了自己的布道点的位置。

  3.牧师每一次移动不可能离所有人都更近，有的人发现A牧师移动以后自己还不如去B牧师处听课更近，于是每个居民又去了离自己最近的布道点.....就这样，牧师每个礼拜更新自己的位置，居民根据自己的情况选择布道点，最终稳定了下来。

• 算法步骤

  • 先定义总共有多少个类/簇（cluster）
  • 将每个簇⼼（cluster centers）随机定在⼀个点上
  • 将每个数据点关联到最近簇中⼼所属的簇上
  • 对于每⼀个簇找到其所有关联点的中⼼点（取每⼀个点坐标的平均值）
  • 将上述点变为新的簇⼼
  • 不停重复，直到每个簇所拥有的点不变

• 举例

  • 题⽬：有以下6个点，将A3和A4作为两个簇的初始簇⼼。问最后的簇的所属情况
  • 

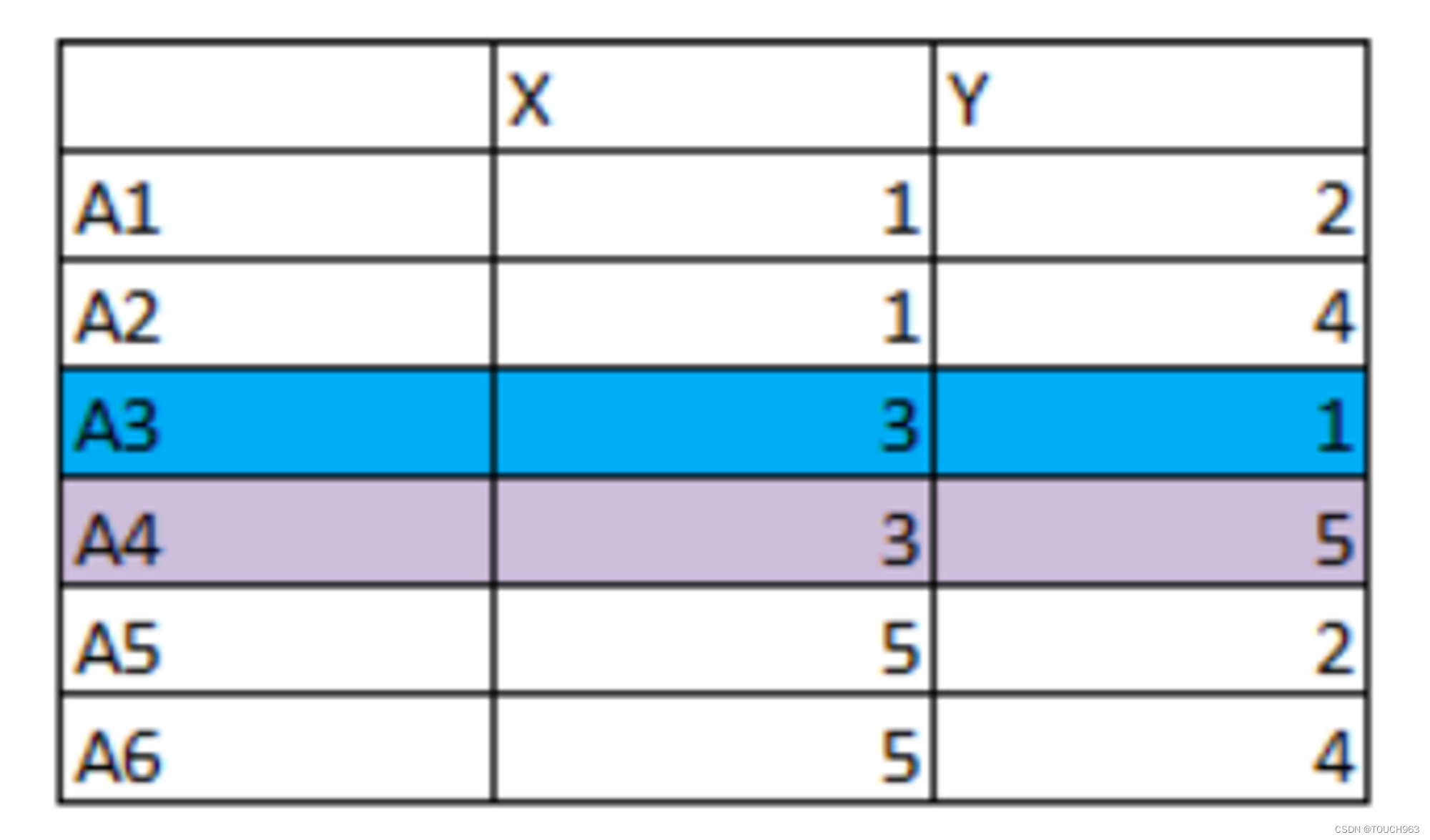
  1.计算每个点到簇⼼距离（根据距离公式），将距离近的点归为⼀类 

• 

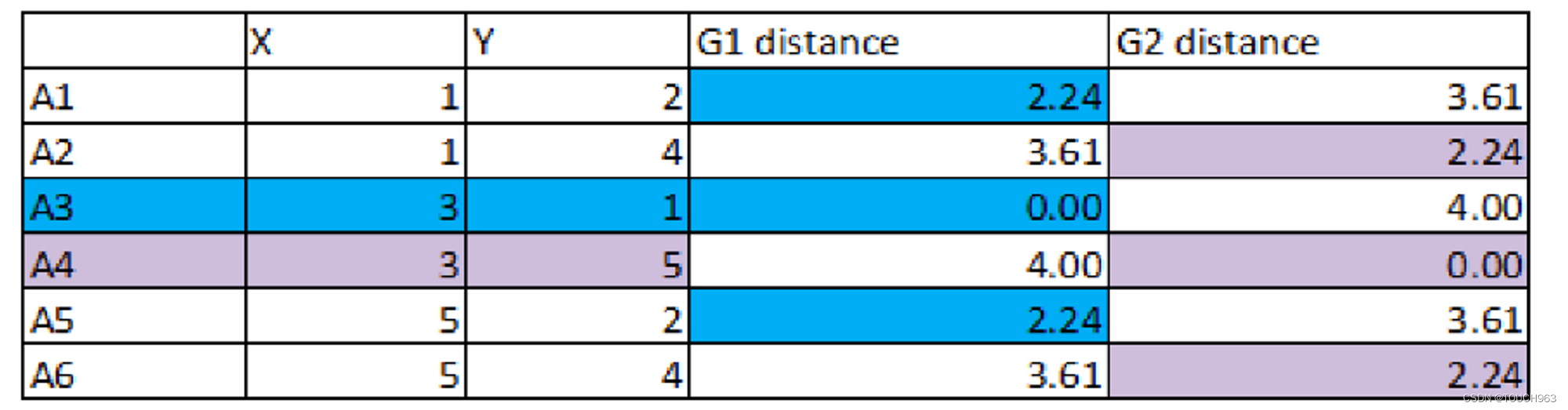
   2.将蓝⾊每个点，和紫⾊每个点的X,Y值分别求平均。获得新的簇⼼

• 

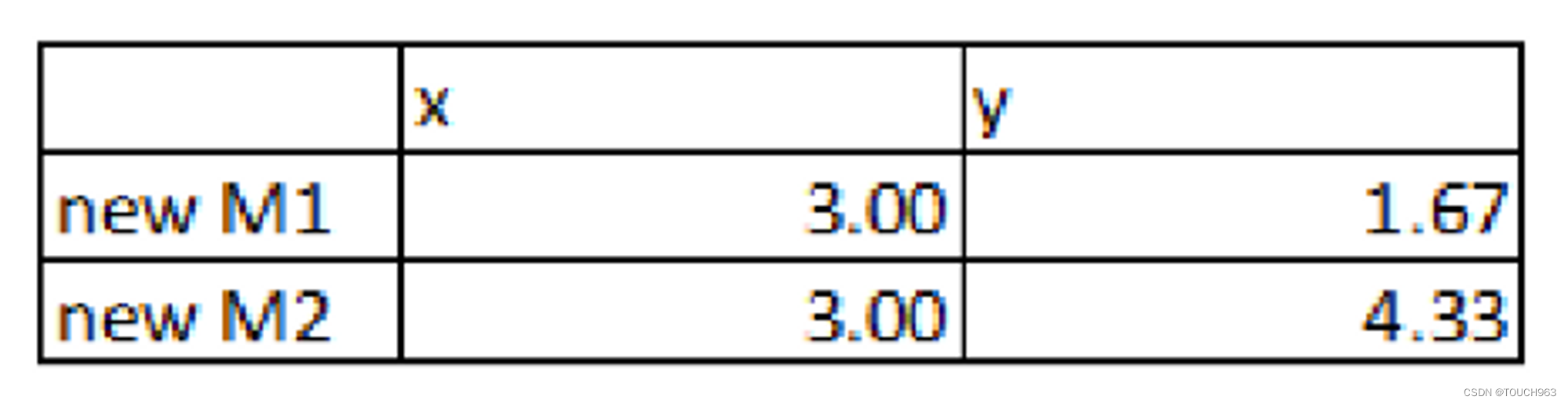
   3.计算每个点到簇⼼的新距离，将距离近的点归为⼀类

• 

   

  4.由于关联点没有变化，所以之后的计算结果不会改变。停⽌计算。

  如果关联的点有变化，则会重复1-3的步骤直到关联点不变。

• 5.蓝⾊簇:A1,A3,A5。紫⾊簇：A2,A4,A6。