写在前头
凸优化问题(OPT,convex optimization problem)指定义在凸集中的凸函数最优化的问题。一般形式为:
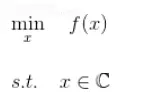
凸优化问题
虽然凸优化的条件比较苛刻,但仍然在机器学习参数最优化领域有广泛的应用。凸优化问题的优势体现在:
1、凸优化问题的局部最优解就是全局最优解
2、很多非凸问题都可以被等价转化为凸优化问题或者被近似为凸优化问题
3、凸优化问题的研究较为成熟,当一个具体被归为一个凸优化问题,基本可以确定该问题是可被求解的
相关理论
凸集
定义:
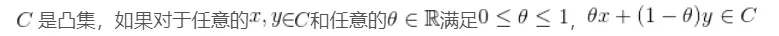
凸集定义
几何意义:

凸集的几何意义
凸函数
定义:

凸函数定义
几何意义:
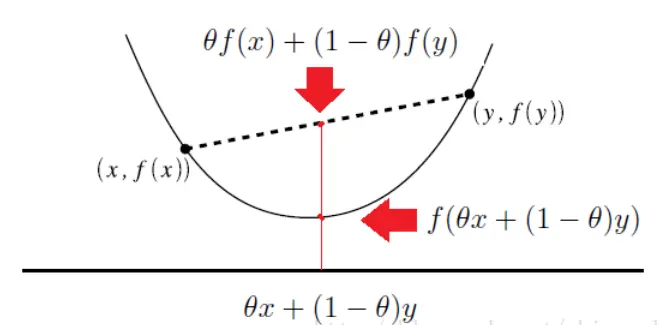
凸函数几何意义
凸函数的一阶充要条件:
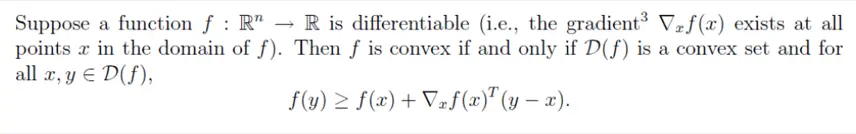
一阶充要条件

几何意义:定义域内的所有函数值都大于等于该点的一阶近似
凸函数的二阶充要条件:

凸函数的二阶充要条件
凸优化问题
定义:

凸优化问题定义
常见的凸优化问题
线性规划(LP,Linear Program)
二次规划(QP,Quadratic Program)
二次约束的二次规划(QCCP,Quadratically Contrained Quadratic Program)
半正定规划(SDP,Semidefinite Program)
机器学习中的凸优化
凸优化的过程
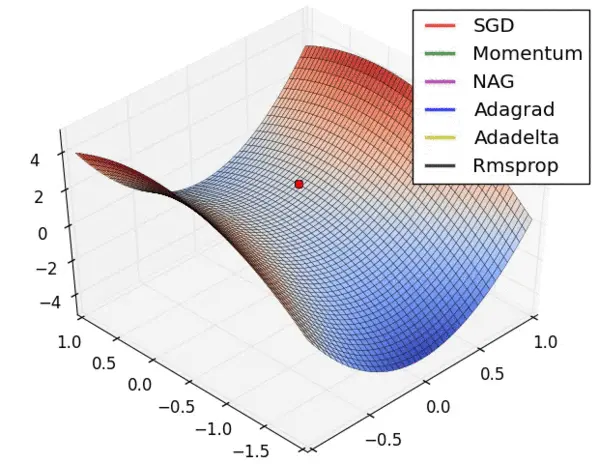
多种机器学习方法的优化求解
凸优化的求解过程可以概括为:找到一个点列使得函数值一直减少,直到达到停止的条件或某个最小值。
数学描述

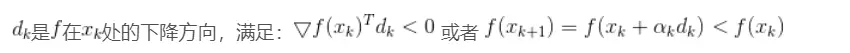




 本文深入探讨了凸优化问题的基本概念,包括凸集与凸函数的定义及其几何意义,介绍了凸优化问题的优势,并列举了几种常见的凸优化问题类型。此外,文章还详细阐述了凸优化在机器学习参数最优化领域的应用。
本文深入探讨了凸优化问题的基本概念,包括凸集与凸函数的定义及其几何意义,介绍了凸优化问题的优势,并列举了几种常见的凸优化问题类型。此外,文章还详细阐述了凸优化在机器学习参数最优化领域的应用。
















 1368
1368

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








