贝叶斯应用_拼写检查器

初衷

• P(c), 文章中出现一个正确拼写词 c 的概率, 也就是说, 在英语文章中, c 出现的概率有多大
• P(w|c), 在用户想键入 c 的情况下敲成 w 的概率. 因为这个是代表用户会以多大的概率把 c 敲错成 w
• argmaxc, 用来枚举所有可能的 c 并且选取概率最大的

step1:导入相关库

import re,collections

step2：将语料库中的数据全部转换为小写且去除其他字符

def words(text):
    return re.findall('[a-zA-Z]+',text.lower())
    #re.findall() 返回text中所有的大小写字母相匹配的全部字串
    #'[a-zA-Z]+' 不分大小写字母的英文单词（无限字母）并且最少是一个字母

step3:统计词在语料库中出现的频率

def train(features):
    model=collections.defaultdict(lambda:1) 
    #匿名函数 用一个很小的概率(出现次数最少为1次)来代表拼写完全正确但语料库中无该词的情况
    for f in features:
        model[f]+=1 
        #每出现1次+1
    return model

step4:读取语料库数据

NWORDS = train(words(open('big.txt').read()))
NWORDS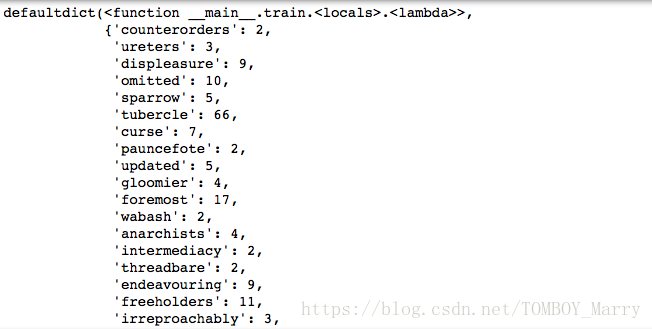

step5:定义alphabet

alphabet='abcdefghjklmnopqrestcvygbhnjkmln'

step6:编辑距离为1

#两个词之间的编辑距离定义为使用了几次插入(在词中插入一个单字母)，
#删除(删除一个单字母), 交换(交换相邻两个字母), 
#替换(把一个字母换成另一个)的操作从一个词变到另一个词.
#返回所有与单词 w 编辑距离为 1 的集合
def edits1(word):
    n = len(word)
    return set([word[0:i]+word[i+1:] for i in range(n)] +  #删除一个字符
               [word[0:i]+word[i+1]+word[i]+word[i+2:] for i in range(n-1)] + #交换位置
               [word[0:i]+c+word[i+1:] for i in range(n) for c in alphabet] + # 替换
               [word[0:i]+c+word[i:] for i in range(n+1) for c in alphabet])  # 插入

step7:编辑距离为2

#返回所有与单词 w 编辑距离为 2 的集合
def edits2(word):
    return set(e2 for e1 in edits1(word) for e2 in edits1(e1))

step8:处理编辑距离为0，1，2的情况

def known(words): 
    return set(w for w in words if w in NWORDS) #编辑距离为0

#如果known(set)非空, candidate 就会选取这个集合, 而不继续计算后面的
def correct(word):
    candidates = known([word]) or known(edits1(word)) or known_edits2(word) or [word]
    return max(candidates, key=lambda w: NWORDS[w]) #返回概率最大的情况

step9:使用拼写检查器

correct('knon')

输出为 ‘non’

correct('morw')

输出为 ‘more’