【无标题】

​
树可以看作是一个连通且无环的无向图。

给定往一颗n个结点(结点值1~n)的树中添加一条边后的图。添加的边的两个顶点包含在1到n中间，且这条附加的边不属于树中已存在的边。

图的信息记录于长度为n的二维数组edges，edges[i] = [a, b]表示图中在a和b之间存在一条边。

请找出一条可以删去的边，删除后可以使得剩余部分是一个有着n个结点的树。如果有多个可以删去的边，则输出数组edges中最后出现的那条边。

​​在这里插入图片描述

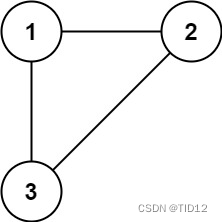
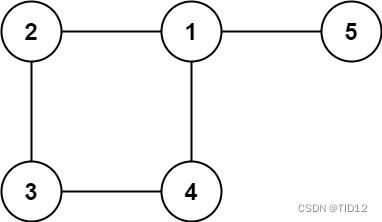
第一行输入t，表示有t个测试样例。

接着，输入n，接着输入长度为n的edges数组。

以此类推，共输入t个测试样例。

每一行输出当前测试样例的结果。

共输出t行。

input

3

3
1 2
1 3
2 3

5
1 2
2 3
3 4
1 4
1 5

8
1 8
4 8
1 2
1 3
4 5
4 6
3 5
5 7

output

2 3
1 4
3 5

**解题思路：**运用并查集的思想把每一个输入的都合并成一个祖先，如果输入的这两个找到的是同一个祖先那就把他们存起来，题目要求的是输出的最后的两个边，所以后续有找到就继续更新

并查集的模板

查找：

int find(int x)
{
	if (fa[x] == x)
		return x;
	else
		return find(fa[x]);
}

合并：

fa[find(a)] = find(b);

以下是ac代码

#include<iostream>
using namespace std; 
int fa[50] = { 0 };
int find(int x)
{
	if (fa[x] == x)
		return x;
	else
		return find(fa[x]);
}

int main()
{
	int t;
	cin >> t;
	while (t--)
	{
		int r1, r2;
		for (int i = 0; i < 50; i++)
		{
			fa[i] = 0;
		}//初始化fa的数组
		int n;
		cin >> n;
		for (int i = 0; i < n; i++)
		{
			fa[i] = i;
		}//初始化并查集
		int a, b;
		for (int i = 0; i < n; i++)
		{
			cin >> a >> b;
			if (find(a) != find(b))//将每次输入的两个数去找他们的祖先，如果不一样就将他们合并
				fa[find(a)] = find(b);
			else
			{
				r1 = a;
				r2 = b;//如果一样就说明这两条边连起来会构成一个环就不合并，并且将他们的数值记录下来
			}
		}
		cout << r1 << " " << r2;
		if (t != 0)
		{
			cout << endl;
		}
	}
}```