矢量积与反对称矩阵：理论、性质与Python实现_向量反对称矩阵几何-优快云博客

在向量代数与矩阵理论中，矢量积（叉乘）与反对称矩阵之间存在着深刻而优雅的数学联系。这种联系不仅揭示了三维空间的几何结构，还为物理应用（如刚体力学）提供了强大的数学工具。本文将系统探讨这两者的定义、性质、相互关系以及在Python中的数值与符号实现。

矢量积的数学本质

在三维欧几里得空间 $R3\mathbb{R}^3$ 中，两个向量 $a=[a1,a2,a3]⊤\mathbf{a} = [a_1, a_2, a_3]^\top$ 和 $b=[b1,b2,b3]⊤\mathbf{b} = [b_1, b_2, b_3]^\top$ 的矢量积定义为：

$\mathbf{a} \times \mathbf{b} = \begin{bmatrix} a_2b_3 - a_3b_2 \\ a_3b_1 - a_1b_3 \\ a_1b_2 - a_2b_1 \end{bmatrix}$

这个运算具有深刻的几何意义：结果向量 $c\mathbf{c}$ 垂直于 $a\mathbf{a}$ 和 $b\mathbf{b}$ 张成的平面，其模长 $∣a×b∣=∣a∣∣b∣sin⁡θ|\mathbf{a} \times \mathbf{b}| = |\mathbf{a}||\mathbf{b}|\sin\theta$ 等于两向量构成的平行四边形面积。代数上，矢量积满足反交换律 $a×b=−b×a\mathbf{a} \times \mathbf{b} = -\mathbf{b} \times \mathbf{a}$ ，且与点积形成标量三重积 $a⋅(b×c)\mathbf{a} \cdot (\mathbf{b} \times \mathbf{c})$ ，其几何意义是平行六面体的有向体积。

反对称矩阵的理论框架

一个 $\times n$ 实矩阵 $A$ 被称为反对称矩阵（或斜对称矩阵），当且仅当它满足：

$A^\top = -A$

此定义蕴含两个直接推论：

主对角线元素满足 $aii=−aii⇒aii=0a_{ii} = -a_{ii} \Rightarrow a_{ii} = 0$
非对角线元素满足 $a_{ij} = -a_{ji}$

三维空间中的反对称矩阵具有标准形式：

$[\mathbf{\omega}]_\times = \begin{bmatrix} 0 & -\omega_3 & \omega_2 \\ \omega_3 & 0 & -\omega_1 \\ -\omega_2 & \omega_1 & 0 \end{bmatrix}$

其中仅需三个独立参数 $(ω1,ω2,ω3)(\omega_1, \omega_2, \omega_3)$ 即可完全确定矩阵。这种形式揭示了反对称矩阵与三维向量的同构关系——两者构成相同维度的向量空间。

反对称矩阵的深层性质

反对称矩阵展现出丰富而独特的代数特性：

行列式特性：奇数阶反对称矩阵的行列式恒为零：
$\det(A) = \det(A^\top) = \det(-A) = (-1)^n \det(A) = -\det(A) \Rightarrow \det(A) = 0 \quad (n \text{ odd})$
偶数阶行列式则是其元素的Pfaffian的平方。
谱特性：特征值呈纯虚数或零，且成共轭对出现 $±iλk\pm i\lambda_k$ 。对于 $\times n$ 矩阵，特征值满足：
$\lambda_k = -\overline{\lambda_k} \quad \text{且} \quad \sum \lambda_k = \operatorname{tr}(A) = 0$
秩的奇偶性：反对称矩阵的秩恒为偶数，这是其规范型的推论：
$Q^\top A Q = \bigoplus_{k=1}^{r/2} \begin{bmatrix} 0 & -\lambda_k \\ \lambda_k & 0 \end{bmatrix} \oplus \mathbf{0}$
其中 $λk>0\lambda_k > 0$ ， $\operatorname{rank}(A)$ 为偶数。
指数映射：反对称矩阵的矩阵指数生成特殊正交群 $SO (n)$ ：
$\exp(A) \in SO(n) = \{ R \in O(n) \mid \det R = 1 \}$
这一性质构成李群理论的基础，其中 $A$ 对应李代数 $so(n)\mathfrak{so}(n)$ 的元素。

矢量积与反对称矩阵的深刻联系

三维空间中，矢量积与反对称矩阵通过以下构造建立一一对应：

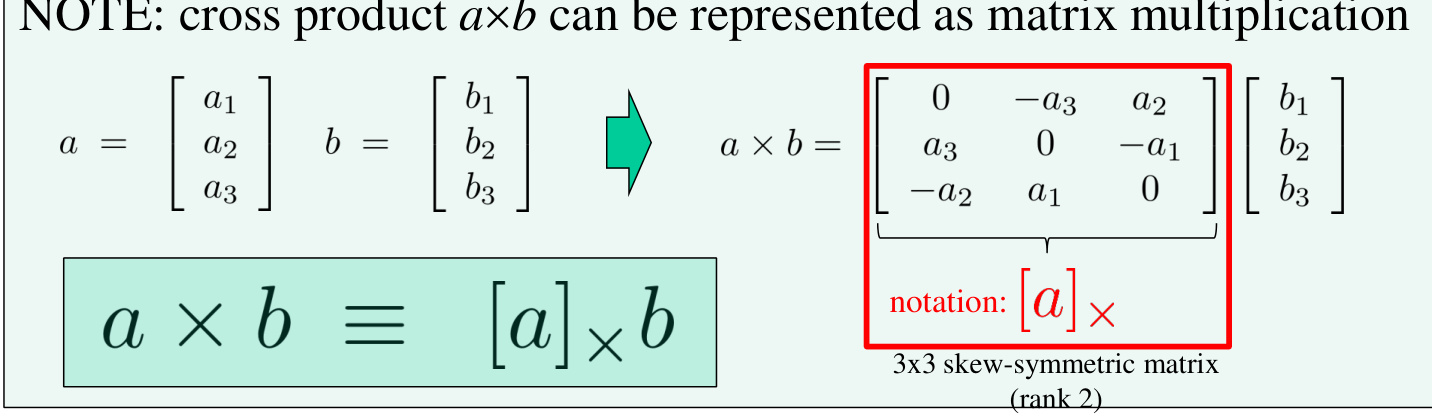
$\mathbf{a} \times \mathbf{b} = [\mathbf{a}]_\times \mathbf{b}$

其中 $[a]×[\mathbf{a}]_\times$ 是由 $a\mathbf{a}$ 生成的反对称矩阵。这一等式可通过直接计算验证：

$[\mathbf{a}]_\times \mathbf{b} = \begin{bmatrix} 0 & -a_3 & a_2 \\ a_3 & 0 & -a_1 \\ -a_2 & a_1 & 0 \end{bmatrix} \begin{bmatrix} b_1 \\ b_2 \\ b_3 \end{bmatrix} = \begin{bmatrix} a_2b_3 - a_3b_2 \\ a_3b_1 - a_1b_3 \\ a_1b_2 - a_2b_1 \end{bmatrix}$

这种等价性在物理学中极为重要：

角速度 $ω\boldsymbol{\omega}$ 产生的线速度： $v=ω×r=[ω]×r\mathbf{v} = \boldsymbol{\omega} \times \mathbf{r} = [\boldsymbol{\omega}]_\times \mathbf{r}$
力矩计算： $τ=r×F=[r]×F\boldsymbol{\tau} = \mathbf{r} \times \mathbf{F} = [\mathbf{r}]_\times \mathbf{F}$
无穷小旋转生成元： $\approx I + \theta [\mathbf{u}]_\times$

Python实现：数值与符号计算

NumPy数值计算实现

import numpy as np
from scipy.linalg import expm

# 矢量积计算
a = np.array([1, 2, 3])
b = np.array([4, 5, 6])
cross_product = np.cross(a, b)  # 输出: [-3, 6, -3]

# 反对称矩阵生成
def skew_symmetric(v):
    return np.array([[0, -v[2], v[1]], 
                    [v[2], 0, -v[0]], 
                    [-v[1], v[0], 0]])

A_skew = skew_symmetric(a)  # 与a对应的反对称矩阵
cross_via_matrix = A_skew @ b  # 矩阵乘法实现叉积

# 性质验证
assert np.allclose(A_skew.T, -A_skew)  # 反对称性
assert np.isclose(np.linalg.det(A_skew), 0)  # 行列式为0
eigvals = np.linalg.eigvals(A_skew)  # 特征值: [0, ±i√14]

# 指数映射生成旋转矩阵
theta = np.pi/2  # 90度旋转
axis = np.array([0, 0, 1])  # z轴
R = expm(theta * skew_symmetric(axis))
# 输出: [[0,-1,0], [1,0,0], [0,0,1]]

SymPy符号计算实现

from sympy import symbols, Matrix, det, eye

# 符号向量定义
ax, ay, az, bx, by, bz = symbols('a_x a_y a_z b_x b_y b_z')
a_sym = Matrix([ax, ay, az])
b_sym = Matrix([bx, by, bz])

# 矢量积计算
cross_sym = a_sym.cross(b_sym)  # [ay*bz - az*by, ...]

# 反对称矩阵生成
def skew_symmetric_sym(v):
    return Matrix([[0, -v[2], v[1]], 
                  [v[2], 0, -v[0]], 
                  [-v[1], v[0], 0]])
                  
A_skew_sym = skew_symmetric_sym(a_sym)
cross_matrix_sym = A_skew_sym @ b_sym  # 与cross_sym等价

# 性质验证
assert A_skew_sym.T == -A_skew_sym  # 反对称性
assert det(A_skew_sym).simplify() == 0  # 行列式为0

# 指数映射解析计算
theta_sym = symbols('theta')
u_sym = Matrix([0, 0, 1])  # z轴单位向量
A_rot = theta_sym * skew_symmetric_sym(u_sym)
R_sym = A_rot.exp()  # 符号旋转矩阵

物理与几何应用

刚体旋转运动学

角速度 $ω\boldsymbol{\omega}$ 与位置矢量 $r\mathbf{r}$ 的关系：
$\mathbf{v} = \boldsymbol{\omega} \times \mathbf{r} = [\boldsymbol{\omega}]_\times \mathbf{r}$
此公式可直接推广到刚体上任意点的速度计算。

旋转矩阵参数化

Rodrigues公式建立了旋转轴角与旋转矩阵的显式联系：
$\exp(\theta [\mathbf{u}]_\times) = I + \sin\theta [\mathbf{u}]_\times + (1-\cos\theta)[\mathbf{u}]_\times^2$
其中 $u\mathbf{u}$ 是单位旋转轴向量。

高维推广：格拉斯曼代数

在 $n$ 维空间中，反对称矩阵自然对应外代数中的双向量：
$\mathbf{a} \wedge \mathbf{b} \leftrightarrow A = \mathbf{a}\mathbf{b}^\top - \mathbf{b}\mathbf{a}^\top$
这种推广保留了反对称性 $A⊤=−AA^\top = -A$ ，并将叉积概念扩展到高维空间。

结论

矢量积与反对称矩阵的对应关系揭示了三维欧几里得空间的深层代数结构。这种对应不仅提供了计算工具，更成为连接向量代数、矩阵理论、李群李代数的桥梁。在物理应用中，反对称矩阵形式简化了旋转动力学描述；在数学上，它提供了叉积向高维推广的自然框架。通过Python的数值与符号计算实现，我们能在具体问题中有效利用这些理论工具，从刚体力学到计算机图形学，展现了这一数学结构的强大应用价值。

反对称矩阵的普适性质——秩的偶性、特征值的虚性、指数映射的正交性——使其成为理解旋转变换本质的关键。正如赫尔曼·外尔所言：“对称性是宇宙的数学语言”，而反对称性则是描述旋转与手性的基本语法。