python第二次作业

原创已于 2025-07-29 18:48:25 修改 · 779 阅读

8 ·

CC 4.0 BY-SA版权

文章标签：

#python #java #算法

于 2025-07-18 23:05:59 首次发布

1.技术面试题

（1）详细描述单调栈的工作原理和应用场景

答：单调栈是一种特殊的栈结构，其核心特性是栈内元素始终保持单调性（递增或递减）。其工作原理如下：

1.初始化：创建一个空栈，用于存储元素（通常是数组的索引或值）。
2.遍历元素：依次处理输入序列中的每个元素。
3.维护单调性：
对于单调递增栈，若当前元素小于栈顶元素，则弹出栈顶元素，直到栈顶元素小于当前元素或栈为空。
对于单调递减栈，若当前元素大于栈顶元素，则弹出栈顶元素，直到栈顶元素大于当前元素或栈为空。
4.压入当前元素：确保新元素入栈后，栈的单调性不被破坏。
结果记录：在弹出元素时，可根据问题需求记录相关信息（如距离、边界等）。
单调栈的应用场景：
单调栈常用于解决与“下一个更大/更小元素”、“边界问题”或“区间极值”相关的问题。以下是典型应用场景：

1.下一个更大元素
给定一个数组，为每个元素找到其右侧第一个更大的元素。例如 LeetCode 496（Next Greater Element I）。

2.柱状图中的最大矩形
利用单调栈快速找到每个柱子左右两侧最近的更低柱子，计算以当前柱子为高的最大矩形面积（LeetCode 84）。

3.接雨水问题
通过单调栈确定每个位置的左右边界，计算可接的雨水量（LeetCode 42）。

4.滑动窗口最大值
单调栈的变种（单调队列）可用于高效求解滑动窗口的最大值（LeetCode 239）。

（2）详细描述单调队列的工作原理和应用场景

答：单调队列是一种特殊的队列，队列中的元素保持单调递增或单调递减的顺序。它的核心思想是通过维护队列的单调性，快速获取当前窗口或范围内的极值（最大值或最小值）。单调队列通常用于滑动窗口类问题。

单调队列的操作主要包括入队和出队：

入队时，从队列尾部开始移除破坏单调性的元素，再将新元素加入尾部。
出队时，检查队首元素是否已超出窗口范围，若超出则移除。

单调队列的时间复杂度为O(n)，因为每个元素最多被入队和出队一次。

单调队列的应用场景：
1.滑动窗口最大值/最小值
单调队列最常见的应用是解决滑动窗口中的极值问题。例如，给定一个数组和一个窗口大小，要求滑动窗口时快速获取每个窗口的最大值或最小值。

2.优化动态规划问题
在某些动态规划问题中，单调队列可以优化状态转移的时间复杂度。例如，解决限制步长的最大子数组和问题时，单调队列可以快速获取区间内的极值。

3.解决区间极值查询问题
单调队列可以高效处理离线区间极值查询问题，例如多次查询固定长度区间的最小值或最大值。

2.HR面试题

（1）如果竞争对手用双倍薪资挖你，你会怎么选择？

答：对我来说，职业选择的核心是平台能否帮助我持续成长，而薪资只是其中的一个因素。如果贵司的岗位能提供我期望的发展空间、团队协作环境以及长期价值，即使其他公司提供高薪，我仍然会优先选择与自己的职业规划更契合的机会。毕竟，只有双方价值观一致，才能走得更远

（2）我们觉得你今天表现一般，不符合岗位要求，你有什么想说的？

答：感谢您的反馈。我理解今天的表现可能没有完全展现我的潜力

3.选择题

（1）在Python中，以下哪个不是循环控制语句？

A. break
B. continue
C. pass
D. return

答：C

（2）以下代码的输出结果是什么？

for i in range(5):
    if i == 3:
        continue
    print(i, end=' ')

A. 0 1 2 3 4
B. 0 1 2 4
C. 0 1 2
D. 3

答：B

（3）完成以下代码，使其能够打印出1到100之间所有的偶数：

for i in range(1, 101):
    if ______:
        print(i, end=' ')

A. i % 2 == 0
B. i % 2 == 1
C. i / 2 == 0
D. i // 2 == 0

答：A

（4）以下代码有一个错误，导致它无法正确计算1到10的和。请选择正确的修改方案：

sum = 0
i = 1
while i < 10:
    sum += i
    i += 1
print(sum)

A. 将i < 10改为i <= 10
B. 将i += 1改为i += 2
C. 将sum += i改为sum = sum + i + 1
D. 将i = 1改为i = 0

答：A

（5）以下代码的输出结果是什么？

for i in range(3):
    for j in range(2):
        print(f"({i},{j})", end=' ')

A. (0,0) (0,1) (1,0) (1,1) (2,0) (2,1)
B. (0,0) (1,0) (2,0) (0,1) (1,1) (2,1)
C. (0,0) (0,1) (0,2) (1,0) (1,1) (1,2)
D. (0,0) (1,1) (2,2)

答：A

（6）完成以下代码，使其能够打印出斐波那契数列的前10个数：

a, b = 0, 1
for _ in range(10):
    print(a, end=' ')
    ______

A. a, b = b, a + b
B. a, b = a + b, b
C. a, b = b, a
D. a, b = a + 1, b + 1

答：A

（7）以下代码的输出结果是什么？

i = 0
while i < 5:
    i += 1
    if i == 3:
        continue
    print(i, end=' ')
else:
    print("Done")

A. 1 2 3 4 5 Done
B. 1 2 4 5 Done
C. 1 2 4 5
D. 1 2 Done

答：B

（8）以下代码的输出结果是什么？

for i in range(1, 5):
    for j in range(1, 5):
        if i * j > 10:
            break
        print(f"{i}*{j}={i*j}", end=" ")
    print()

1*1=1 1*2=2 1*3=3 1*4=4 
2*1=2 2*2=4 2*3=6 2*4=8 
3*1=3 3*2=6 3*3=9 3*4=12 
4*1=4 4*2=8 4*3=12 4*4=16

1*1=1 1*2=2 1*3=3 1*4=4 
2*1=2 2*2=4 2*3=6 2*4=8 
3*1=3 3*2=6 3*3=9 
4*1=4 4*2=8

1*1=1 1*2=2 1*3=3 1*4=4 
2*1=2 2*2=4 2*3=6 2*4=8 
3*1=3 3*2=6 3*3=9

1*1=1 1*2=2 1*3=3 1*4=4 
2*1=2 2*2=4 2*3=6 2*4=8

答：B

（9）以下代码的输出结果是什么？

for i in range(4):
    for j in range(4):
        if (i + j) % 2 == 0:
            print("*", end="")
        else:
            print("#", end="")
    print()

****
####
****
####

*#*#
#*#*
*#*#
#*#*

*#*#
*#*#
*#*#
*#*#

****
****
****
****

答：B

（10）以下代码的输出结果是什么？

count = 0
for i in range(1, 5):
    for j in range(1, 5):
        for k in range(1, 5):
            if i != j and j != k and i != k:
                count += 1
print(count)

A. 24
B. 36
C. 60
D. 64

答：A

4.问答题

（1）Python中有哪几种基本的循环结构？请简要说明它们的语法和适用场景。

答：Python 提供了两种主要的循环结构：for 循环和 while 循环。它们分别适用于不同的场景，以下是它们的详细说明。

for循环：

for 变量 in 可迭代对象：
循环体

1.适用于已知循环次数或需要遍历可迭代对象（如列表、元组、字符串、字典等）的情况。
2.常用于遍历序列或集合中的元素，执行固定次数的操作。

while循环：

while 条件:
循环体

1.适用于不确定循环次数的情况，只要条件为真就会继续执行循环。
2.常用于需要根据条件动态控制循环次数的场景，如游戏循环或用户输入验证。

（2）Python中有哪些循环控制语句？它们各自的作用是什么？请给出示例说明。

答：Python 还提供了 break 和 continue 语句来控制循环流程：

break 用于完全退出循环。
continue 用于跳过当前循环的剩余部分，直接进入下一次循环。

循环与 else 语句
Python 允许在 for 或 while 循环后使用 else 语句，当循环正常结束（未被 break 中断）时执行。

（3）在Python的for循环中，range()函数扮演着重要角色。请详细说明range()函数的语法、参数含义和使用方法，并给出至少3个不同用法的示例。

答：range()函数语法
range(start, stop[, step])
该函数生成一个不可变的整数序列，通常用于循环迭代。参数均为整数类型，其中start和step为可选参数。

参数含义：
start：序列起始值（默认为0，包含在序列中）
stop：序列结束值（不包含在序列中，必须提供）
step：步长（默认为1，可为负数实现倒序）

基本用法示例：
1.单参数（仅stop）
生成0到4的序列（共5个数字，不包含5）：
for i in range(5):
print(i) # 输出: 0, 1, 2, 3, 4

2.双参数（start和stop）
生成3到7的序列（不包含7）：
for i in range(3, 7):
print(i) # 输出: 3, 4, 5, 6

3.三参数（含step）
生成1到10的偶数序列（步长为2）：
for i in range(1, 10, 2):
print(i) # 输出: 1, 3, 5, 7, 9

4.倒序序列
通过负步长实现从5到1的倒序：
for i in range(5, 0, -1):
print(i) # 输出: 5, 4, 3, 2, 1

5.结合列表生成式
将range()结果转为列表：
numbers = list(range(0, 10, 3))
print(numbers) # 输出: [0, 3, 6, 9]

6.控制循环次数
重复特定次数的操作（如打印3次消息）：
for _ in range(3):
print(“Hello”) # 输出3次"Hello"

（4）什么是嵌套循环？请解释嵌套循环的工作原理。

答：
嵌套循环：
嵌套循环是指在一个循环结构内部包含另一个循环结构。外层循环每执行一次，内层循环会完整执行一遍。嵌套循环常用于处理多维数据或需要多重迭代的场景，例如遍历二维数组、生成乘法表等。

工作原理：
外层循环的每次迭代会触发内层循环的全部执行。内层循环完成后，外层循环才会进入下一次迭代，直到外层循环终止。

（5）编写代码，判断两个矩形的关系

题目描述

判断两个矩形之间的关系：包含，重叠，相离

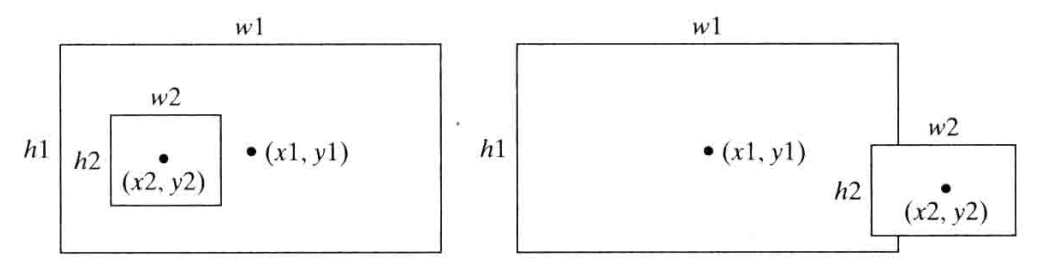
输入输出描述

输入两行，每行四个数据，分别是矩形的中心坐标x、y和矩形的宽、高

输出两者的关系

示例1

输入：

2.5 4 2.5 43

1.5 5 0.5 3

输出：

包含

示例2

输入：

1 2 3 5.5

3 4 4.5 5

输出：

重叠

示例3

输入：

1 2 3 3

40 45 3 2

输出：

相离

答：

# 在此写入你的代码
# 输入两个矩形的数据
x1, y1, w1, h1 = map(float, input().split())
x2, y2, w2, h2 = map(float, input().split())

# 计算矩形1的边界
left1 = x1 - w1 / 2
right1 = x1 + w1 / 2
top1 = y1 + h1 / 2
bottom1 = y1 - h1 / 2

# 计算矩形2的边界
left2 = x2 - w2 / 2
right2 = x2 + w2 / 2
top2 = y2 + h2 / 2
bottom2 = y2 - h2 / 2

# 判断包含关系
if (left1 <= left2 and right1 >= right2 and bottom1 <= bottom2 and top1 >= top2) or \
   (left2 <= left1 and right2 >= right1 and bottom2 <= bottom1 and top2 >= top1):
    print("包含")
# 判断相离关系
elif (right1 < left2 or left1 > right2 or top1 < bottom2 or bottom1 > top2):
    print("相离")
# 否则为重叠
else:
    print("重叠")

（6）编写代码，打印如下数字图案

                        1
                    1	2	1
                1	2	4	2	1
            1 	2	4	8	4	2	1
        1	2	4	8	16	8	4	2	1
    1	2	4	8	16	32	16	8	4	2	1
1	2	4	8	16	32	64	32	16	8	4	2	1

答：

# 在此写入你的代码
n = 7  # 总行数

for i in range(1, n + 1):
    # 打印前导空格（每行减少4个空格）
    print('    ' * (n - i), end='')
    
    # 打印左半部分数字（1, 2, 4, 8...）
    for j in range(1, i + 1):
        print(2 ** (j - 1), end='\t')
    
    # 打印右半部分数字（...8, 4, 2, 1）
    for j in range(i - 1, 0, -1):
        print(2 ** (j - 1), end='\t')
    
    # 换行
    print()

（7）编写代码，打印如下星星图案

    *
   ***
  *****
 *******
*********
 *******
  *****
   ***
    *

答：

# 在此写入你的代码
n = 5  # 上半部分的行数

# 打印上半部分
for i in range(n):
    print(' ' * (n - i - 1) + '*' * (2 * i + 1))

# 打印下半部分
for i in range(n - 2, -1, -1):
    print(' ' * (n - i - 1) + '*' * (2 * i + 1))

（8）编写代码，求最小公倍数

题目描述

输入两个正整数，计算其最小公倍数，例如4和2的最小公倍数是4，3和5的最小公倍数是15

输入输出描述

输入两个正整数

输出最小公倍数

示例1

输入：

3 9

输出：

9

示例2

输入：

4 6

输出：

12

答：

# 在此写入你的代码
def gcd(a, b):
    while b:
        a, b = b, a % b
    return a

def lcm(a, b):
    return abs(a * b) // gcd(a, b)

# 示例测试
print(lcm(4, 2))  # 输出4
print(lcm(3, 5))  # 输出15