【算法】AcWing算法基础课笔记第一章基础算法 Part 1-优快云博客

本文链接：https://blog.youkuaiyun.com/Summerison/article/details/131640006

本文是作者对AcWing算法基础课的学习笔记，主要介绍了快速排序和归并排序这两种常用排序算法的详细步骤与代码实现，并涵盖了整数二分查找的原理和代码。作者采用分治策略解释了这两种排序算法的工作原理，并提供了C++实现的示例代码。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

🚀Write In Front🚀
📝个人主页：令夏二十三
🎁欢迎各位→点赞👍 + 收藏⭐️ + 留言📝
📣系列专栏：AcWing
💬总结：希望你看完之后，能对你有所帮助，不足请指正！共同学习交流 🖊

文章目录

前言

我在大一下时，为了准备蓝桥杯买了AcWing的这套算法基础课，当时只看了前两章的内容，到现在已经隔了好几个月没有练习算法了，模板都生疏了不少，于是想趁暑假有时间，将这套课完整地看完，并记好笔记，在C站上打卡。

学习课程时，我完整地听完视频，不懂的地方会找题解和博客的思路来理解，每道题的算法模板也会重复敲上三五遍，最后再自己总结笔记。

今天是我打卡算法学习的第一天，希望接下来可以坚持下去，系统地学完！

本篇笔记主要介绍了两类基础算法，分别是排序和二分，各自还有细分的算法模板，下面让我们一起学习吧。

一、排序算法

我们都知道有八大排序，但是在这里只介绍两种最常用的算法，分别是快速排序和归并排序。

1. 快速排序

快速排序，简称快排，由于它在诸多排序算法中的时间复杂度最小，因此在程序中使用耗时最短，故称之为快速。

排序，就是将一组无序的数字排成从小到大的有序序列，

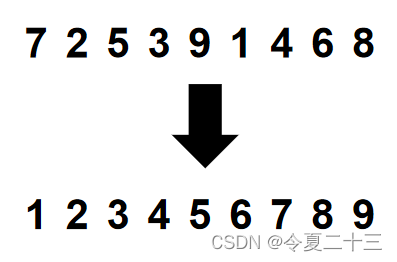
怎么做呢？不同的排序算法各有其独特思路，快速排序的核心思路就是分治。

分治，就是分而治之，先将无序序列分成小、中、大三个部分，从左至右排序，然后对其中的每个部分又按这个方法来排序，先从整体上看有序，到最后最小的细节也有序了，就完成了排序。

具体步骤详解

首先，随机选择序列中的一个数，将其作为排序的分界点：

然后，在序列中设置指针，分别指向序列的第一个数和最后一个数：

接下来，如果左边指针所指向的数小于5，则指针向右移动一位，否则停下；若右边指针所指向的数大于5，则向左移动一位，否则也停下。

当两个指针都停下时，交换两个指针所指向的数。

若指针指向的数相同，也就是都移动到了分界点，一次排序就结束了，得到大致有序的序列：

接下来就是对分界点两侧的序列进行同样的排序，每次排序后都可以得到一个更有序的序列，直到序列完全有序：

在实际的代码中，上面的多次细化排序是通过递归实现的。

代码

#include<iostream>
using namespace std;

const int N=1e6+10;
int n;
int q[N];

void quick_sort(int q[],int l,int r)//l和r分别是数组的左端和右端 
{
	if(l>=r) return;//当数组的右端不大于左端时，可知数组中的数最多只有一个，无需再排序了 
	int x=q[(l+r)/2],i=l-1,j=r+1;//选取x为分界点，i是左指针，j是右指针 
	while(i<j)//当i还在j的左边时，排序尚未结束，需要继续排 
	{
		do i++;while(q[i]<x);//这里的do语句配合了上面i和j的设置，就可以先移动指针，再进行判断 
		do j--;while(q[j]>x);
		if(i<j) swap(q[i],q[j]);//swap函数可以交换数组中下标分别为i和j的位置的数值 
	}
	quick_sort(q,l,j); 
	quick_sort(q,j+1,r);//这里分别对分界点左边部分和右边部分再细致排序 
}

int main()
{
	cin>>n;
	for(int i=0;i<n;i++) cin>>q[i];
	quick_sort(q,0,n-1);
	for(int i=0;i<n;i++) cout<<q[i]<<" ";
	return 0;
}

2. 归并排序

归并排序的中心思想和快排一样，还是分治，但是这里的分治不太一样。

在快排里，我们先排序再递归，而归并则是先递归再排序。

具体步骤详解

归并的过程其实就像它的名字一样，先递归，再合并，合并的过程就是排序的过程。

通过递归，可以将一组无序的序列拆分成若干组只含一个数的序列：

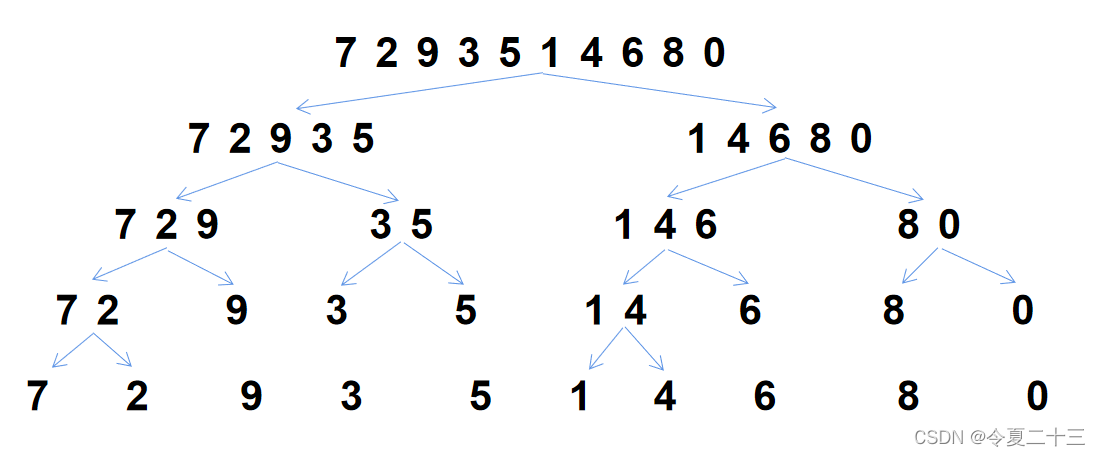
由图中可看出，每次递归都将序列从中间分成两部分，中间的数归属于左边部分。

接下来，再从递归的最后开始，也就是上图的最后一层开始，逐步将序列两两合并，每次都合并得到一个有序序列，到最后就可以完成排序：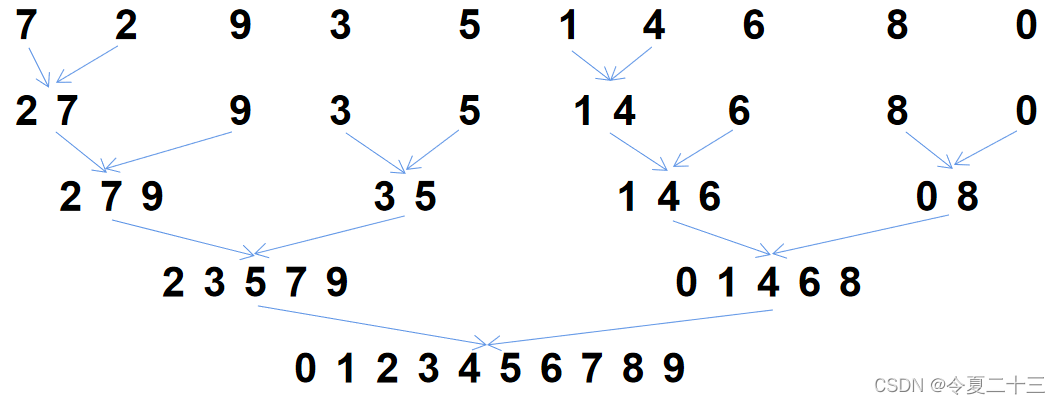

代码

#include<iostream>
using namespace std;

const int N=1e6;
int n;
int q[N],tmp[N];//这里的tmp数组用来暂存归并后的数组 

void merge_sort(int q[],int l,int r)
{
	if(l>=r) return;
	int mid=(l+r)/2;//mid为数组的中点，用它来将数组分为两部分 
	merge_sort(q,l,mid);
	merge_sort(q,mid+1,r);//用递归的方法将整个数组拆分成一个个只含一个数的序列 
	int k=0,i=l,j=mid+1;//k作为归并数组中的指针 ，i是左边部分的指针，j是右指针 
	while(i<=mid&&j<=r)
	{
		if(q[i]<=q[j]) tmp[k++]=q[i++];//将较小的数先放入归并数组中 
		else tmp[k++]=q[j++];
	}
	while(i<=mid) tmp[k++]=q[i++];//比较完成后，若某个数组还有剩余的数，容易知道它们是有序的，就直接全部移入即可 
	while(j<=r) tmp[k++]=q[j++];
	for(int i=l,j=0;i<=r;i++,j++) q[i]=tmp[j];//最后将归并数组中的数原封不动地放入原数组 
}

int main()
{
	cin>>n;
	for(int i=0;i<n;i++) cin>>q[i];
	merge_sort(q,0,n-1);
	for(int i=0;i<n;i++) cout<<q[i]<<" ";
	return 0;
}

二、二分算法

二分算法就是二分查找的算法，一般用于查找数或者数的边界，整数和浮点数都可以查找。

1. 整数二分

整数二分用于在可重复的整数序列中查找某个数在序列中的起止点。每次查找会将序列长度折半，从而大大减少查找的次数。

从具体的例子来看，下面这个表格表示存储在数组里的一个递增序列，表格上面的是数组下标，下面是序列，要求查找 2 这个数字在数组中下标的起止点。

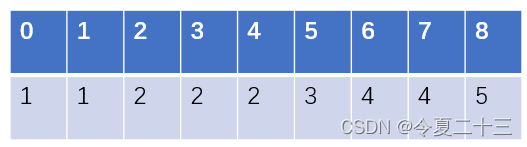
通过两个不同的二分查找函数，我们就可以得到左端和右端的下标，下面我们来看看具体步骤。

具体步骤详解

在二分查找中，我们每一步选取的数都要和要查找的数比较，然后确定更小的范围。

对于例子的这个问题，可以将它分为查找左边界和右边界这两个问题，接下来分别阐述一下左边界和右边界的查找方法。

查找左边界

首先，确定查询为 2 ，接下来就以它为比较的对象，只有等于查询的数，才有可能是边界。

对于左边界，每次的二分就是选取数组中间的那个数，和查询进行比较：

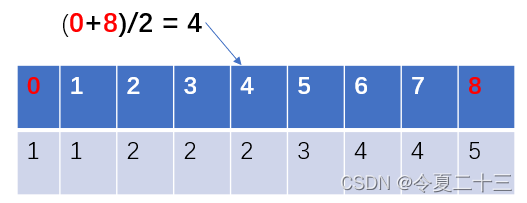
数组中下标为 4 的数为 2 ，接下来就要将这个数和查询比较了，比较要遵循的规则是：

如果选取的数小于查询，说明这个数必然不等于查询，也就不可能是边界，而且这个数必然在左边界的左边，比如上图中下标为 1 的数，这时候就需要缩小查找范围了，缩小的方法就是将查询的起点设置为选取的数的右边的那个数；

如果选取的数大于或等于查询，那就可以直接缩小查找范围了，将查询的终点设置为选取的这个数，因为我们要查找的是左边界，所以可以把右边界忽略掉，只关注数组中从左往右第一个出现的查询。

接下来就是不断循环这个选取和比较的过程，直到我们把范围缩小成一个数，也就是查找的起点和终点的下标相等，这时候就可以得到左边界了。

最后的查找范围会缩小到两个数，也就是起点和终点相邻了，此时使用上面确定中点的方法就可以把范围缩小到起点，最后得到正确的答案。

对于右边界，其实和左边界的查找相差不大，只需要注意几个点：

选取中间数的算法是(起点+终点+1) / 2 ，因为考虑到最后查找时起点和终点相邻，我们要把范围再缩小到终点，这样才能得到右边界；
要得到右边界，所以判断大小时先缩小左边，另一种情况就是选取的数大于查询，这时候就要将查询的终点设置为选取数的左边的那个数。

代码

int search_left(int l,int r,int x)
{
	while(l<r)
	{
		int mid=(l+r)/2;//当l和r指针相邻时，得到的mid就为l 
		if(q[mid]>=x) r=mid;
		else l=mid+1;
	}
	return l;//其实l和r都可以，因为二分终止条件就是r==l 
}

int search_right(int l,int r,int x)
{
	while(l<r)
	{
		int mid=(l+r+1)/2;//当l和r指针相邻时，得到的mid就为r 
		if(q[mid]<=x) l=mid;
		else r=mid-1;//有加必有减（上面l+r+1） 
	}
	return r;
}

2. 浮点数二分

浮点数二分一般用于查找某一特定的浮点数，比如数的三次方根，下面就是求数的三次方根的例子。

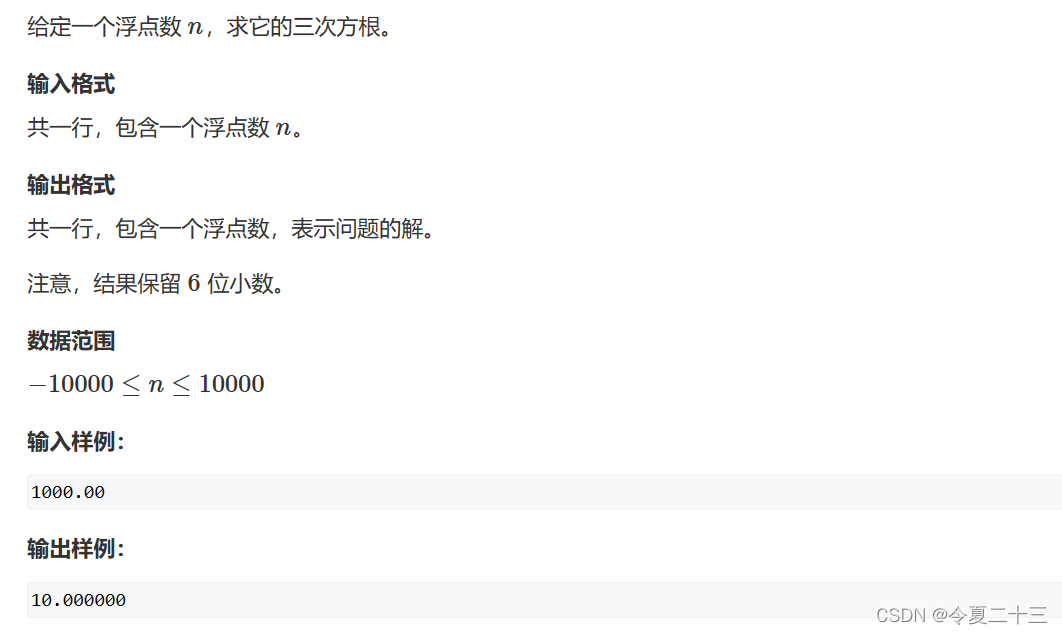
具体步骤详解

上面的数据范围就可以作为查找的范围，由于我们使用的是二分查找，所以也是和整数二分一样，多次折半查找范围，直到求得答案。

但是浮点数二分的答案不是得到数的边界，而是具体的浮点数，然而浮点数的精度是可变的，按照题目的输出格式提示，需要保留6位小数，所以查找的终止条件就是左右边界的距离小于一个六位的小数（如0.000001）

代码

#include<iostream>
#include<iomanip>
using namespace std;
double n,l,r,mid;
int main()
{
	cin>>n;
	l=-10000,r=10000;
	while(r-l>=1e-7)
	{
		mid=(l+r)/2;
		if(mid*mid*mid<=n) l=mid;
		else r=mid;
	}
	cout<<fixed<<setprecision(6)<<l;
	return 0;
}