一、算法概述
算法性质
算法是由若干条指令组成的有穷序列,且满足下述4条性质:
① 输入:有零个或多个由外部提供的量作为算法的输入;
② 输出:算法产生至少一个量作为输出;
③ 确定性:组成算法的每条指令是清晰的,无歧义的;
④ 有限性:算法中每条指令的执行次数是有限的,执行每条指令的时间也是有限的。
程序是算法用某种程序设计语言的具体实现。可以不满足性质④。
NP完全性理论
P类问题
— 可以在多项式内求解的【判定问题】。 P类问题是确定性计算模型下的易解问题类。
NP类问题
— 所有的非确定性多项式时间可解的【判定问题】构成NP类问题 。
— 非确定性计算模型下的易验证问题类。
非确定性算法:非确定性算法将问题分解成猜测和验证两个阶段。算法的猜测阶段是非确定性的,算法的验证阶段是确定性的,它验证猜测阶段给出解的正确性。
NPC问题
NP中的某些问题的复杂性与整个类的复杂性相关联,这些问题中任何一个如果存在多项式时间的算法,那么所有NP问题都是多项式时间可解的.
======================================================================================
P ≠ NP ,至今无明确的解答。
NPC问题举例
1、合取范式的可满足性问题 (CNF-SAT)
布尔可满足性问题 ( Boolean Satisfiability Problem , SAT ) , 是 NPC 的 ;
2、三元合取范式的可满足性问题 ( 3-SAT 或 3-CNF-SAT)
3、团问题CLIQUE

4、顶点覆盖问题 (VERTEX-COVER)
给定一个 无向图 G,G 的 点集覆盖 定义 ;找到 无向图 G 的 点集子集 V ,使得无向图 G 中的任何一条边 , 都与 点集子集 V 的至少一个节点是接触的 ;
5、子集和问题 (SUBSET-SUM)
给定一个自然数集合, 给定一个自然数 t, 问给定的自然数集合中,是否存在子集, 使它们之和等于给定的自然数 t
6、哈密顿回路问题 (HAM-CYCLE)
**给定一个图G=(V,E), 是否存在一条路线,从一个起点出发,找到一条回路,每个顶点且只走过一次**
7、旅行售货员问题 (TSP)
无向图中 , 每条边都有一个权重 , 求是否有一条哈密顿路径的权重之和 , 不超过给定的自然数 W
二、排序算法
1、插入排序
插入排序图解
转载-插入排序(图解)
2、归并排序
3、渐近记号
【对于给定的函数 g(n) 】
O - 渐近上界
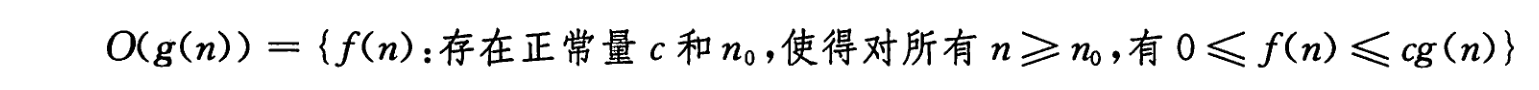
Ω - 渐近下界
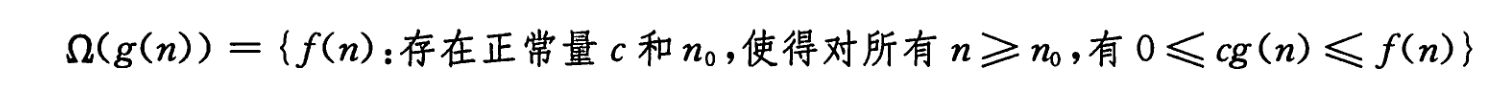
Θ - 渐近紧确界

三、递归与分治
(一)递归
1、概念 ★
递归函数 :用函数自身给出定义的函数
递归中的【递】即【入栈】,递进;【归】–>【出栈】,回归。
递归算法:一个算法包含对自身的调用 (这种调用可以是直接的,也可以是间接的)
【优点】结构清晰,可读性强,易用数学归纳法证明
【缺点】运行效率较低
2、示例

【相关代码】
// 斐波那契数列的实现
// 1、 递归实现 时间复杂度 —– O(2^N)
int fibo1(int n)
{
if(n == 0 || n == 1) return n;
return fibo1(n - 1) + fibo1(n - 2);
}
// 2、 非递归实现
// 时间复杂度为O(N),空间复杂度为O(N)
int* fibo2(int n)
{
int* pArr = new int[n + 1];
pArr[0] = 0; pArr[1] = 1;
for(int i = 2; i <= n; i++)
pArr[i] = pArr[i - 1] + pArr[i - 2];
return pArr;
}
// 时间复杂度为O(N),空间复杂度为O(1)
int fibo3(int n)
{
int nFirst = 0, nSecond = 1, nThird = 0;
for(int i = 2 ; i <= n; i++) {
nThird = nFirst + nSecond;
nFirst = nSecond;
nSecond = nThird;
}
return nThird;
}
3)整数划分问题
将正整数n表示成一系列正整数之和: n=n1+n2+…+nk,其中n1≥n2≥…≥nk≥1,k≥1
正整数n的这种表示称为正整数n的划分
正整数n的不同的划分个数称为正整数n的划分数p(n)
目标:求正整数n的不同划分个数p(n)
【 引入m,最大加数 ≤ m 的划分个数, 记作q(n,m) 】
1、n==1:m取任意值,只有一种划分{1}
2、m==1:n取任意值,只有一种划分{1+1+1+…+1}
3、n==m:根据划分中是否包含n,分为:
(1)划分中包含n,只有一种{n}
(2)划分中不包含n,这时划分中最大的数字也一定比n小,即n所有的n-1划分
4、n<m:实际上不允许出现n<m情况,这时即为q(n,n) 5、n>m:根据划分中是否包含最大值m,可以分为
(1)包含m 的情况,即{m, {x1,x2,….xi} 且 x1+x2+…+xi=n-m,因此这种情况下为 q(n-m,m)。
(2)划分中不包含m且划分中所有值都比m小,即n的所有(m-1)划分,为 q(n,m-1)
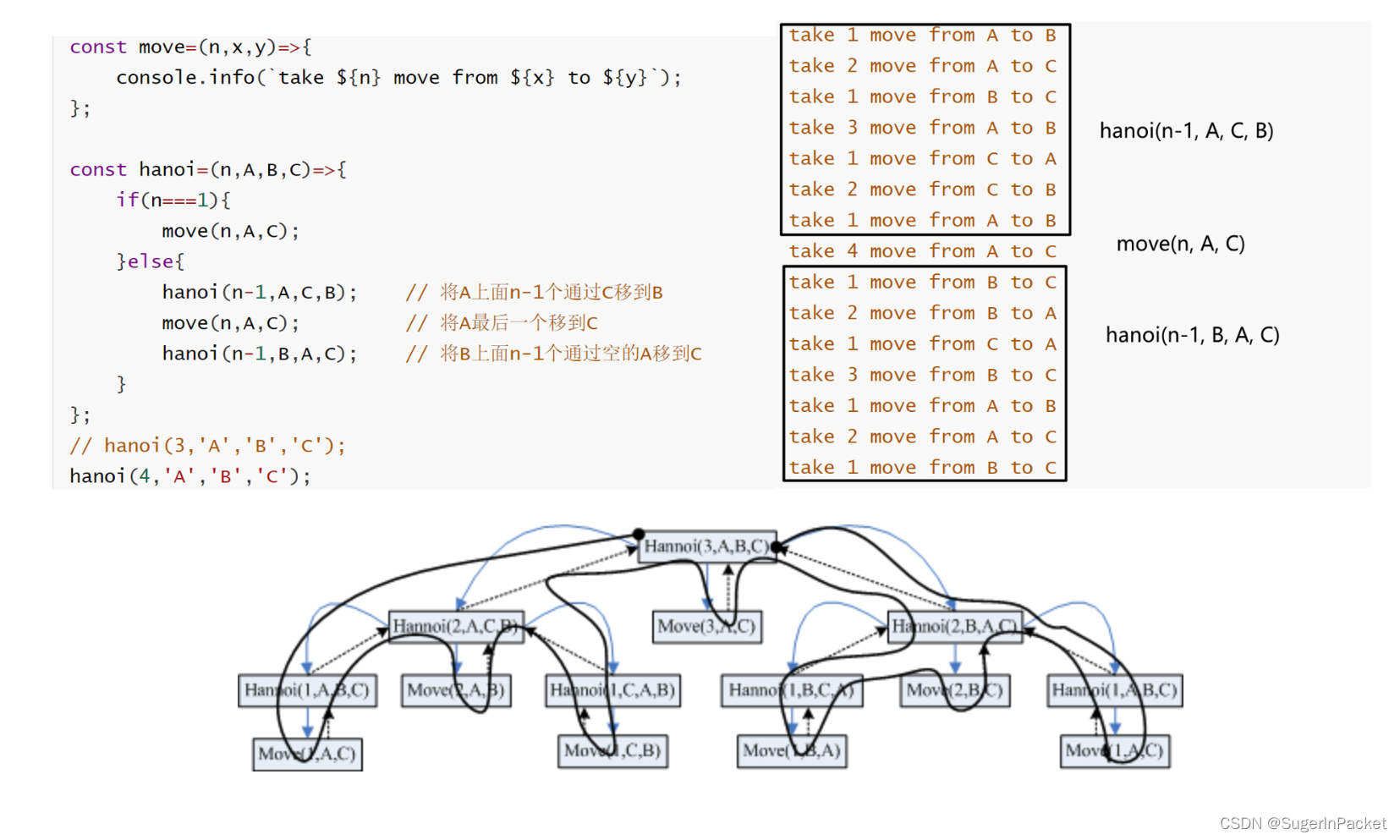
4)汉诺(Hanoi)塔问题
【问题】 有 A,B,C 三根柱子,A 上面有 n 个盘子,我们想把 A 上面的盘子移动到 C 上,但是要满足以下三个条件:① 每次只能移动一个盘子; ② 盘子只能从柱子顶端滑出移到下一根柱子; ③ 盘子只能叠在比它大的盘子上。
【分析】n = 1 时,直接把盘子从 A 移到 C ;
n > 1 时,
先把上面 n - 1 个盘子从 A 移到 B(子问题,递归);
再将最大的盘子从 A 移到 C ;
再将 B 上 n - 1 个盘子从 B 移到 C(子问题,递归)。
2、递归式
递归式的解法
代换法(substitution method) 递归树方法(recursion-tree method) 主方法(master method)
1)代换法(substitution method)
步骤
猜测解的形式 用数学归纳法证明之
2)递归树方法(recursion-tree method)
【参考】https://blog.youkuaiyun.com/yangtzhou/article/details/105339108
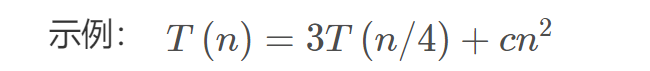
-
3 表示我们将一个问题分解为3 个子问题;
-
n / 4 则表明每个子问题的规模是原问题的1 / 4;
-
T( ) 表明的为递归形式;
-
c n^2 表明为合并需要的时间,其中c为常数系数c > 0 。其实也就是算法度Θ ( n^2 )

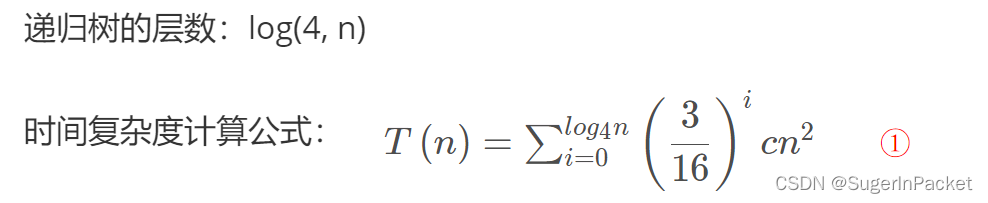
3)主方法(master method)
T(n) = a T(n/b) + f(n)
a>=1, b>1, a和b均为常数 ,f(n)是渐近正函数


(二)分治法
【基本策略】
分解(Divide):将原问题分解为子问题
解决(Conquer):求解子问题
合并(Combine):组合子问题的解得到原问题的 解
【设计思想】将一个难以解决的大问题分割成一些规模较小的相同子问题。
【适用条件】
问题一般具有以下特征
问题的规模缩小到一定程度就可以容易地解决
问题可以分解为若干个规模较小的相同问题,即该 问题具有最优子结构性质
基于子问题的解可以合并为原问题的解
问题所分解出的各个子问题是相互独立的,即子问题之间不包含公共的子问题
【平衡】
—— 使子问题规模尽量接近的做法
在使用分治法和递归时,要尽量把问题分成规模相等,或至少是规模相近的子问题以提高算法的效率
实例
1)二分搜索(Binary search)

2)乘法
① 指数运算 —— 求 a^n
直接求解:Θ(n)
分治法求解:
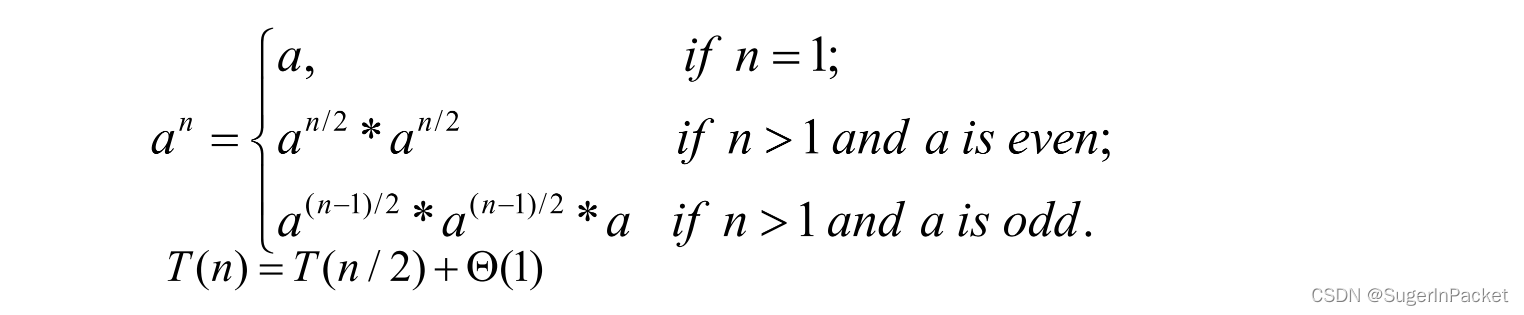
② 大整数乘法

3)快速排序算法
QuickSort(A,p,r)
if p<r
q = Partition(A,p,r) //确定划分位置
QuickSort(A,p,q-1) //子数组A[p...q-1]
QuickSort(Q,q+1,r) //子数组A[q+1...r]
end
//快速排序关键过程是对数组进行划分,划分过程需要选择一个主元素(pivot element)作为参照,围绕着这个主元素进划分子数组
Partition(A,p,r) //p、r为数组下标
x = A[r] //将最后一个元素作为主元素
i = p-1 // i指向的是比主元素小的位置,
for j = p to r-1 //从第一个元素开始到倒数第二个元素结束,比较确定主元素的位置
do if A[j] <= x
then i = i+1 //如果比主元素小,则把i=i+1的位置上的元素和j位置发现小元素互换
exchange A[i] <-> A[j]
exchange A[i+1]<->A[r] //最终确定主元的位置
return i+1 //返回主元的位置
end
快速排序的随机化版本: 随机选择一个元素作为主元
4)Fibonacci数列 — 矩阵法
F(n) = F(n-1) + F(n-2)
递归算法:
自底向上,依次计算 ==> Θ(n)
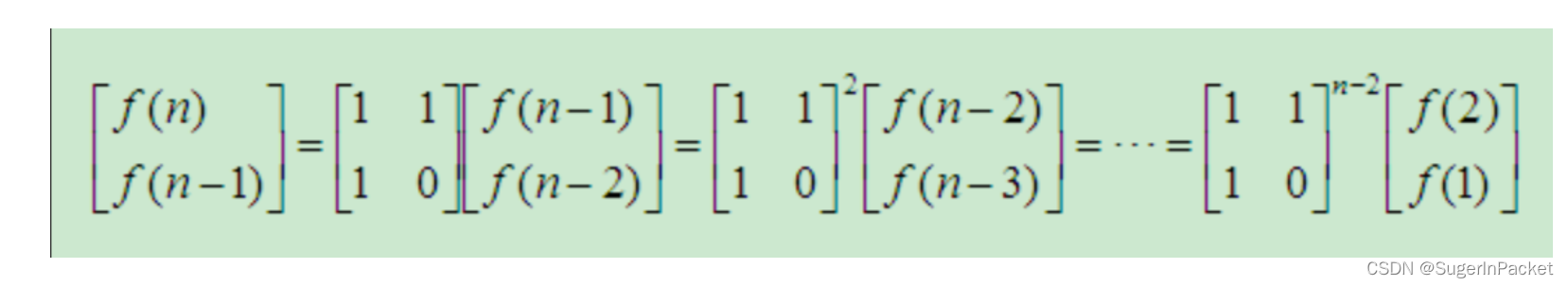
5)矩阵乘法
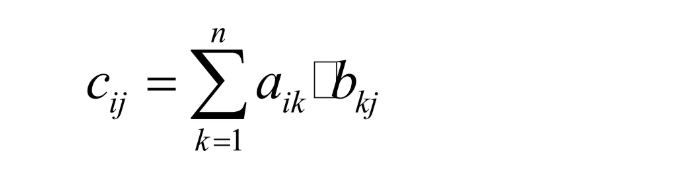
① 3个for循环 — 时间复杂度 O(n^3)
② Strassen的策略

6)最大元、最小元
void max_min(int a[],int l,int r,int &max,int &min){
int n=r-l+1;
int p=n/2;
if(n==1) { //只有一个元素
max=a[l];
min=a[l];
}
else if(n==2){ //只有两个元素
max=a[l]>a[r] ? a[l]:a[r];
min=a[l]<a[r] ? a[l]:a[r];
}
else { //有大于两个元素时
int lmax,lmin,rmax,rmin;//左边最大元、最小元、右边最大元、最小元
max_min(a,l,p,lmax,lmin);//求左边的最大元和最小元
max_min(a,p+1,r,rmax,rmin);//求右边的最大元和最小元
max=lmax>rmax ? lmax:rmax;
min=lmin<rmin ? lmin:rmin;
}
}
7)最近点对问题
① 一维

② 二维
【参考】
leetcode-612
https://blog.youkuaiyun.com/qq_40452317/article/details/88403397
https://blog.youkuaiyun.com/qq_41891805/article/details/105709605
8)寻找顺序统计量问题
在一个由元素组成的集合里,第i个**顺序统计量(order statistic)**是该集合第i小的元素。
https://www.cnblogs.com/zhoutaotao/p/4047082.html
① 排序,时间复杂度O(nlogn)
② 快排思想,期望时间复杂度为 O(n)
一般情况 O(N), 最坏情况 O(N^2)
RandomSelect(A,p, q,k) //随机选择统计,以期望线性时间做选择
{
if (p==q) return A[p];
int pivot=Random_Partition(A,p,q);//随机选择主元,把数组进行划分为两部分
int i=pivot-p+1;
if (i==k )return A[pivot];
else if (i<k) return RandomSelect(A,pivot+1,q,k-i);//第k小的数不在主元左边,则在右边递归选择
else return RandomSelect(A,p,pivot-1,k); //第k小的数不在主元右边,则在左边递归选择
}
RANDOMIZED-SELECT(A, p, r, i)
1 if p = r
2 then return A[p]
3 q ← RANDOMIZED-PARTITION(A, p, r)
4 k ← q - p + 1
5 if i = k // the pivot value is the answer
6 then return A[q]
7 elseif i < k
8 then return RANDOMIZED-SELECT(A, p, q - 1, i)
9 else return RANDOMIZED-SELECT(A, q + 1, r, i - k)
③ 改进快排思想
https://www.cnblogs.com/bakari/p/4852452.html
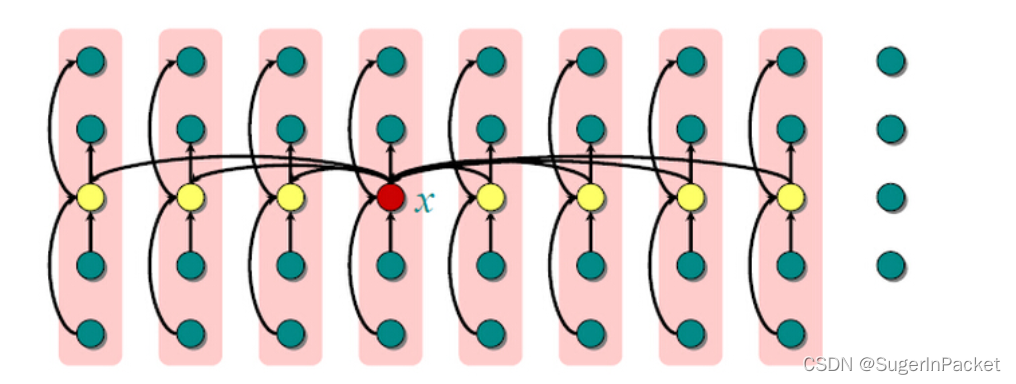
(1)将输入数组的n个元素划分为n/5(上取整)组,每组5个元素,且至多只有一个组有剩下的n%5个元素组成
(2)寻找每个组中的中位数。首先对每组中的元素(至多为5个)进行插入排序,然后从排序后的序列中选择出中位数。
(3)对第2步中找出的n/5(上取整)个中位数,递归调用SELECT以找出其中位数x。(如果是偶数去下中位数)
(4)调用PARTITION过程,按照中位数x对输入数组进行划分。确定中位数x的位置k。
(5)如果i=k,则返回x。否则,如果i<k,则在地区间递归调用SELECT以找出第i小的元素,若干i>k,则在高区找第(i-k)个最小元素。
【分析】所有元素分为 n/5 组,在 x 左右分别有 (n/5) / 2 = n / 10 组,
当 x > k 时,至少有 (n/10) * 3 个数 < x ;当 x < k 时,至少有 (n/10) * 3 个数 > x ;
因此最多在剩余的 7n / 10 个元素中查找,时间为 T (7n/10) ;
综上, T(n) = T(n/5) + T(7n/10) + O(n)
。。。
。。。
四、动态规划
1、基本概念
1)求解对象 —— 最优化问题
工程问题中设计参数的选择 有限资源的合理分配 车间作业调度 交通系统的规划 ……
2)动态规划 vs 分治法
分治法求解回顾
子问题相互独立,不包含公共子问题
动态规划
与分治法类似,也是将问题分解为规模逐渐减小的同类型的子问题
与分治法不同,分解所得的子问题很多都是【重复】的
3)适合用动态规划方法求解的问题
若一个问题可以分解为若干个高度重复的子问题,且问题也具有最优子结构性质, 就可以用动态规划法求解
具体方式:可以递推的方式逐层计算最优值并记录必要的信息,最后根据记录的信息构造最优解
4)总体思想
保存已解决的子问题的答案,在需要时使用,从而避免大量重复计算
2、解题步骤
找出最优解的性质,并刻画其结构特征
递归地定义最优值(写出动态规划方程)
以【自底向上】的递推方式计算出最优值
根据计算最优值时得到的信息,以递归方法构造一个最优解
3、求解实例
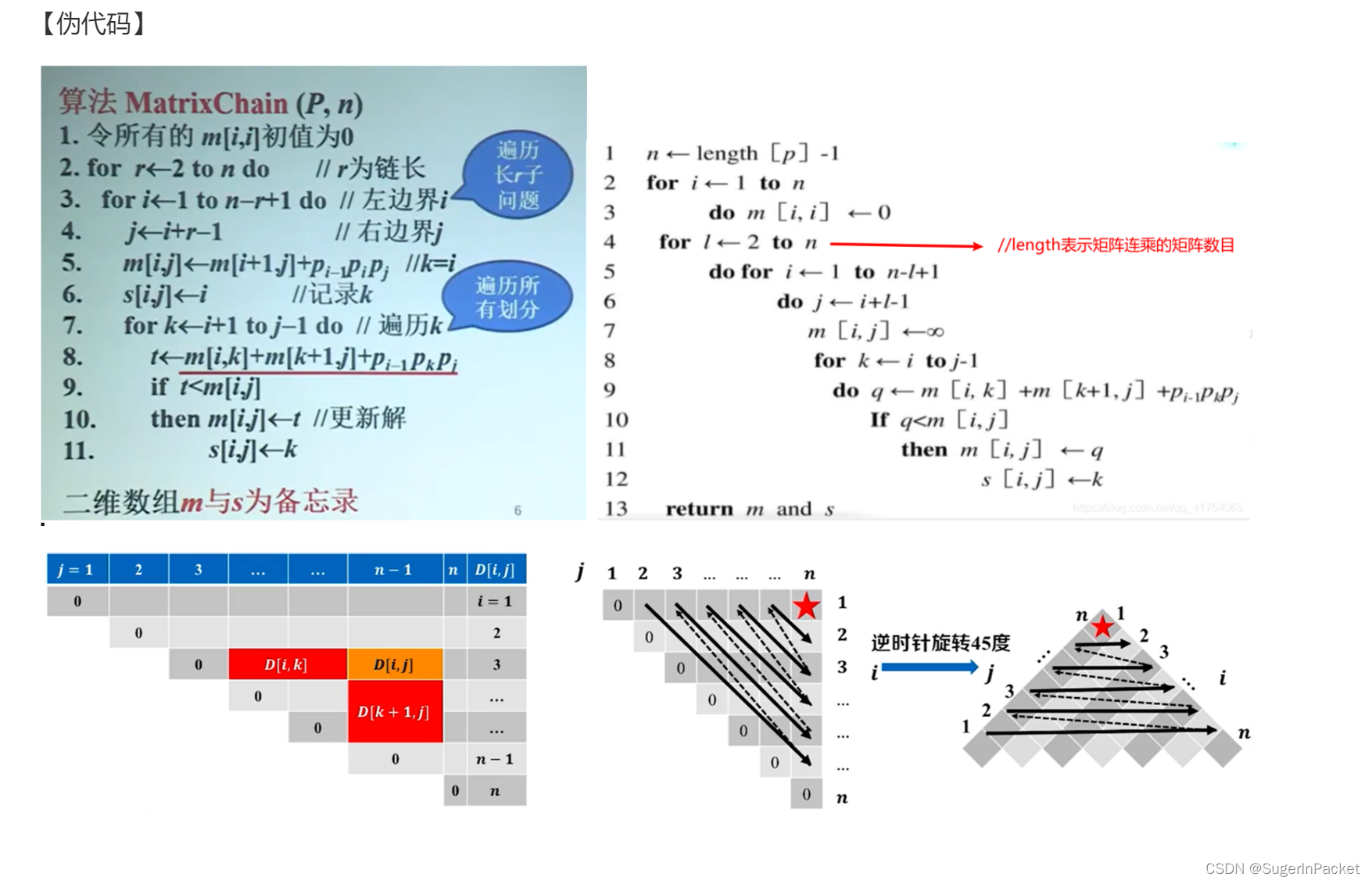
1)矩阵连乘问题
https://www.cnblogs.com/Monster-su/p/14574240.html

2)最长公共子序列问题(LCS)
子序列:将给定序列中零个或多个元素去掉之后得到的结果
子串:给定串中任意个【连续】的字符组成的子序列称为该串的子串
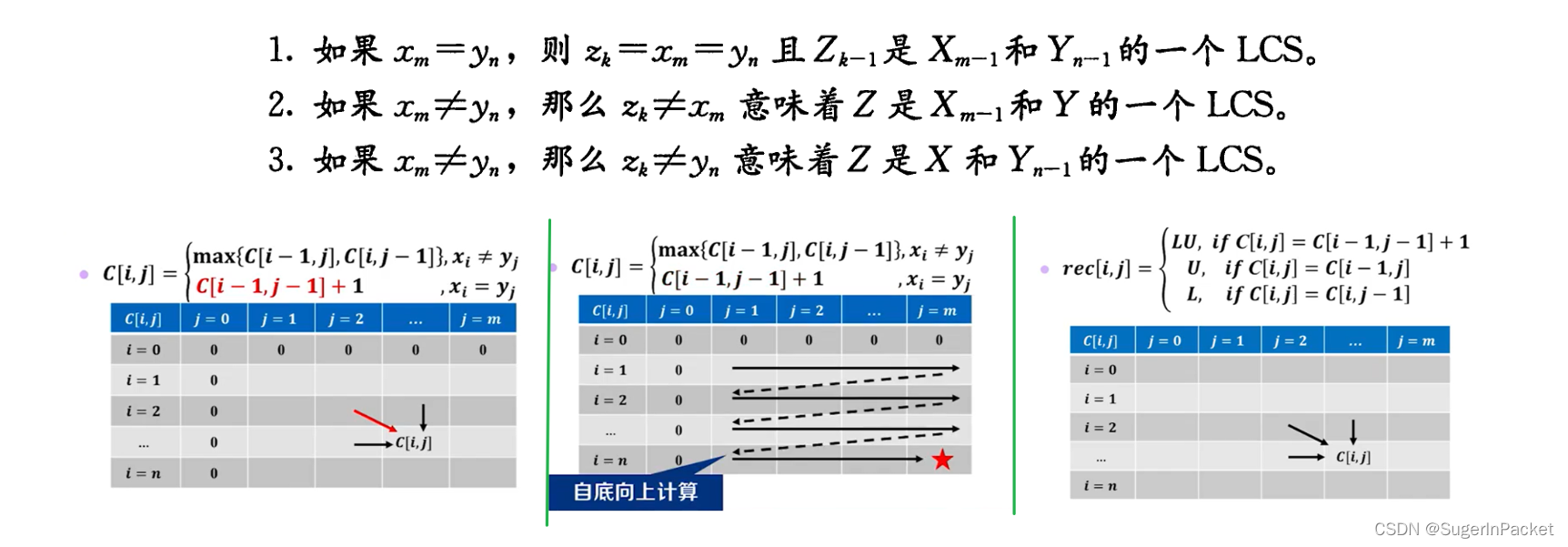
for(int i = 1;i<=m;i++){
for(int j = 1;j<=n;j++){
//i,j从1开始,所以下面用i-1和j-1使得可以从数组0元素开始
if(x[i-1]==y[j-1]) c[i][j] = c[i-1][j-1]+1;
else if(c[i-1][j]>=c[i][j-1]) c[i][j]=c[i-1][j];
else c[i][j]=c[i][j-1];
}
}
https://www.cnblogs.com/Monster-su/p/14579852.html
// 动态规划
public static void f1(char arr1[],char arr2[],int n,int m) {
for(int i=1;i<=n;i++) {
for(int j=1;j<=m;j++) {
if(arr1[i-1]==arr2[j-1])
dp[i][j]=dp[i-1][j-1]+1;
else
dp[i][j]=Math.max(dp[i-1][j], dp[i][j-1]);
}
}
System.out.println(dp[n][m]);
}
// 备忘录
public static int f2(char arr1[],char arr2[],int n,int m) {
if(n==0||m==0) return 0;
else if(arr1[n-1]==arr2[m-1])
dp[n][m]=f2(arr1,arr2,n-1,m-1)+1;
else
dp[n][m]=Math.max(f2(arr1,arr2,n-1,m),f2(arr1,arr2,n,m-1));
return dp[n][m];
}
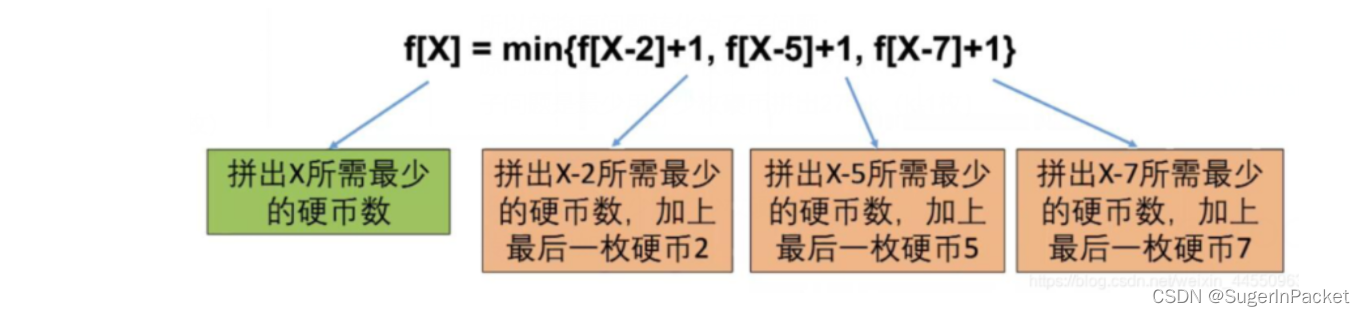
3)子集和问题 —— 硬币计数

https://www.cnblogs.com/wenjieyatou/p/6898876.html
题目:有三种硬币,面值2, 5, 7,买一本书需要27元,如何用最少的硬币整好付清。
4)最优二分搜索树
根据检索频率(包括节点p和虚节点q)设计一颗二叉搜索树,使得期望搜索代价最小。
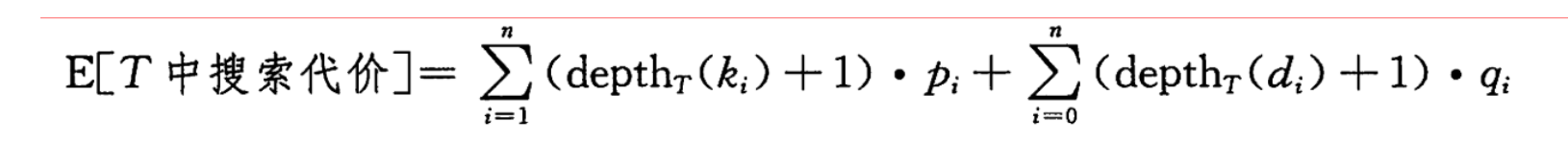
根节点 a[k] 的最有二分搜索树,将左、右子树分别接在根节点下:


【改进 P48】 递推求cij及记录Tij的根的算法可以改进, 把算法时间复杂度从Θ(n3)降到Θ(n2)
5)流水作业调度
参考:https://www.cnblogs.com/wkfvawl/p/11667092.html
最优调度 :① 使M1上的加工是无间断的。即M1上的加工时间是所有ai之和,但M2上不一定是bi之和。
② 使作业在两台机器上的加工次序是完全相同的。
结论:仅需考虑在两台机上加工次序完全相同的调度。

6)备忘录方法
数组中的元素只是在需要计算时才去计算,计算采用递归方式,值计算出来之后将其保存起来以备它用。
备忘录方法是递归方式是【自顶向下】的, 而动态规划是【自底向上】的递归的。
因此备忘录方法的控制结构与直接递归方法的控制结构相同, 区别在于备忘录方法为每个解过的子问题建立了备忘录以备需要时查看,避免了相同子问题的重复求解。
① 备忘录方法 LCS
计算C[i,j]的递归算法LCS_L2(X,Y, i,j,C)
1、 若x[i] == y[j],则去检查C[i-1,j-1]
若C[i-1,j-1]> -1(已经计算出来),就直接把C[i-1,j-1]+1赋 给C[i,j],返回
若C[i-1,j-1]=-1(尚未计算出来),就递归调用LCS_L2(X,Y, i-1,j-1,C) 计算出C[i-1,j-1],然后再把
C[i-1,j-1]+1赋给C[i,j] , 返回
2、若x[i] != y[j],则检查C[i-1,j]和C[i,j-1]
若两者均 > -1(已经计算出来),则把max{ C[i-1,j], C[i,j-1]} 赋给C[i,j],返回
若C[i-1,j], C[i,j-1] 两者中有一个等于-1(尚未计算出来), 或两者均等于-1,就递归调用LCS_L2将其计
算出来,然后 再把max{ C[i-1,j], C[i,j-1]} 赋给C[i,j]
② 最长递增子序列问题
【解一:O(n^2)的dp】
// Dynamic programming.
class Solution {
public int lengthOfLIS(int[] nums) {
if(nums.length == 0) return 0;
int[] dp = new int[nums.length];
int res = 0;
Arrays.fill(dp, 1);
for(int i = 0; i < nums.length; i++) {
for(int j = 0; j < i; j++) {
if( nums[j] < nums[i] )
dp[i] = Math.max(dp[i], dp[j] + 1);
}
res = Math.max(res, dp[i]);
}
return res;
}
【解二:结合LCS】将原序列A排序得到序列B,求A和B的LCS
【解三:贪心 + 二分查找】
https://leetcode-cn.com/problems/longest-increasing-subsequence/solution/zui-chang-shang-sheng-zi-xu-lie-dong-tai-gui-hua-2/
class Solution {
public int lengthOfLIS(int[] nums) {
int len = 1, n = nums.length;
if (n == 0) return 0;
int[] dp = new int[n + 1];
dp[len] = nums[0];
for (int i = 1; i < n; ++i) {
if (nums[i] > d[len]) dp[++len] = nums[i];
else {
int l = 1, r = len, pos = 0;
while (l <= r) {
int mid = (l + r) >> 1;
if (dp[mid] < nums[i]) {
pos = mid; // 更新位置
l = mid + 1;
} else {
r = mid - 1;
}
}
// 【注意】所更新的数组并不是LIS,只是记录了长度
dp[pos + 1] = nums[i];
}
}
return len;
}
}
7)Wavio Sequence
Wavio是一个整数序列,具有如下特性
- Wavio的长度是奇数,即𝐿𝐿 = 2 ∗ 𝑛𝑛 + 1
- Wavio序列的前𝑛𝑛 + 1个整数是一个严格的递增序列
- Wavio序列的后𝑛𝑛 + 1个整数是一个严格的递减序列
- 在Wavio序列中,没有两个相邻的整数是相同的
8)最大子段和

1、简单算法
利用3个for循环,记录所有字段的和,比较所得最大字段和,时间复杂度O(n^3)
2、简单算法改进
从技巧改进,去除最后一层for循环,减少重复计算,时间复杂度O(n^2)
**3、分治策略 ** T(n)=O(nlogn)

4、动态规划 O(n)

9)凸多边形最优三角部分
。。。
10)背包问题
① 0-1背包
// 初始化
for (int j = weight[0]; j <= bagWeight; j++) {
dp[0][j] = value[0];
}
// weight数组的大小 就是物品个数
for(int i = 1; i < weight.size(); i++) { // 遍历物品
for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
if (j < weight[i]) dp[i][j] = dp[i - 1][j];
else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
}
}
// =================================================================================== //
// 【滚动数组】 注意:****** 遍历背包容量的顺序
for(int i = 0; i < weight.size(); i++) { // 遍历物品
for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量 ★★★
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}
② 完全背包
for(int i = 0; i < weight.size(); i++) { // 遍历物品
for(int j = weight[i]; j <= bagWeight; j++) { // 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}
③ 多重背包
n种物品,背包容量M,物品i重量为weight[i],数量有num[i]个,价值为value[i]
④ 混合背包
在基本的0-1背包问题、完全背包和多重 背包的基础上,将三者混合起来。
- 有的物品只可以取一次或者不取(基本的0-1背包)
- 有的物品可以取无限次(完全背包)
- 有的物品可以取得次数有一个上限(多重背包)
⑤ 二维背包
对于每件物品,有两种不同的费用,即装一件物品,需要消耗两种代价
⑥ 分组背包
给出𝑛种物品和一个容量为𝑀的背包,每种物品都有无限件。
这n个物品被划分为若干组,每组中的物品相互冲突,最多选一件放入背包
⑦有依赖的背包
0-1背包加入依赖关系,如果物品𝑖依赖于物品𝑗,则表 示如果要选物品𝑖,则必须先选物品𝑗。
五、贪心算法
1、贪心算法的基本思想
贪心算法并不从整体最优上加以考虑,它所作出的选择只是在某种意义上的**【局部最优选择】**
2、活动安排问题
1)【问题描述】
有一个需要使用每个资源的n个活动组成的集合S= {a1,a2,···,an },资源每次只能由一个活动使用。每个活动ai都有一个开始时间si和结束时间fi,且 0≤si<fi<∞ 。一旦被选择后,活动ai就占据半开时间区间[si,fi)。如果[si,fi]和[sj,fj]互不重叠,则称ai和aj两个活动是兼容的。该问题就是要找出一个由互相兼容的活动组成的最大子集。
2)解决步骤
- 若活动未排序,则按结束时间非递减排序
- 选择相容(若si≥fj或sj≥fi)的活动陆续加入活动安排列表
3、贪心策略的基本要素
1)贪心选择性质
—— 所求问题的整体最优解可以通过一系列局部最优的选择,即贪心选择来达到 。
与dp的区别
- 在动态规划中, 通常以
自底向上的方式解各子问题 ,每步所做的选择往往依赖于相关子问题的解。 - 在贪心算法中, 通常以
自顶向下的方式进行 ,仅在当前状态下做出最好选择,即局部最优选择,然后再去解做出 此选择后产生的子问题。
2)最优子结构性质
—— 一个问题的最优解包含其子问题的最优解
3)贪心算法与动态规划算法的差异
相同点:贪心算法和动态规划算法都要求问题具有最优子结构性质
区别:0-1背包问题,背包问题。
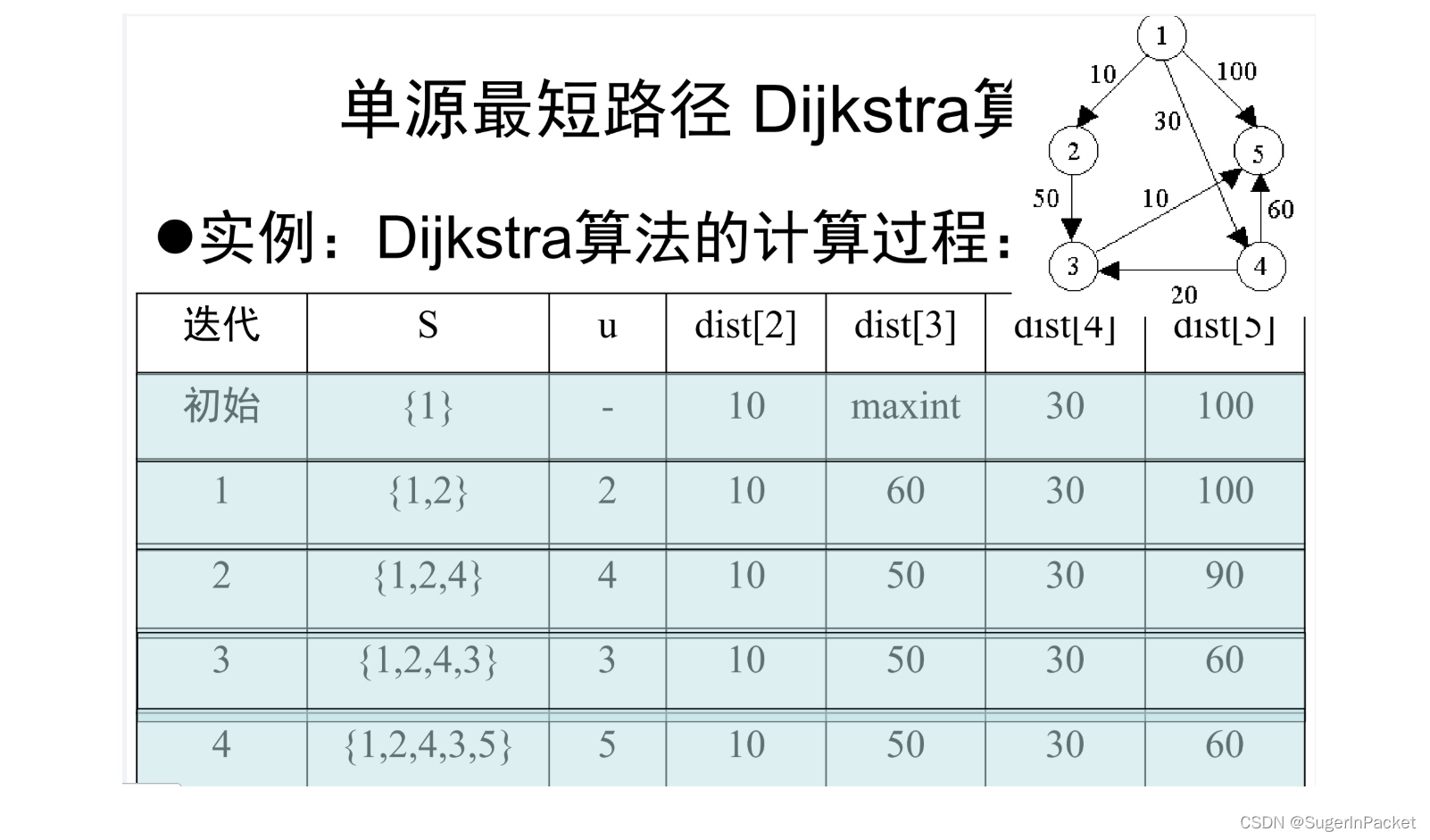
4、贪心算法实例——单源最短路径
【问题描述】:给定 带权有向图 G = <V, E> , 每条边的权是非负实数。计算某点到其他各顶点的最短路长度。
基本思想 o ( n^2 )
设置顶点集合S,初始时,S中仅含有源,此后不断作 贪心选择 来扩充这个集合一个顶点属于集合S当且仅当从源到该顶点的最短路径长度已知设u是G的某一个顶点,把从源到u且中间只经过S中顶 点的路称为从源到u的特殊路径,并用数组dist记录当前每个顶点所对应的最短特殊路径长度Dijkstra算法每次从V-S中取出具有最短特殊路长度的顶点u,将u添加到S中,同时对数组dist作必要的修改, 检查 dist(u)+[u,j] 与 dist[j] 的大小,若 dist(u)+[u,j] 较小,则更新一旦S包含了所有V中顶点,dist就记录了从源到所有其他顶点之间的最短路径长度
5、贪心算法实例——最小生成树
【问题描述】:G =(V,E)是无向连通带权图,即一个网络, E中每条边(v,w)的权为c[v][w], 若G的子图G’是一棵包含G的所有顶点的树,则称G’为G的生成树,生成树上各边权的总和为该生成树的耗费,耗费最小的生成树称为G的最小生成树。
① Prim算法
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-IVcQ7mqQ-1648911071051)(C:\Users\Weller.Y\AppData\Roaming\Typora\typora-user-images\1638599310066.png)]
void Prim(int n, Type **c) {
T = ; S = 1;
while(S != V) {
(i, j) = i∈S且j∈V-S的最小权边;
T = T ∪ {(i ,j)} ;
S = S ∪ {j} ;
}
}
② Kruskal算法
- 首先将G的n个顶点看成n个孤立的连通分支。
- 将所有的边按权值从小到大排序
- 枚举第一个边,加入MST里,判断是否成环
- 如果成环则跳过,否则确定这条边为MST里的
- 继续枚举下一条边,直到所有的边都枚举完
// 把原图中所有边按权值排序
// 初始化MST为空,以及初始化连通分量
for(int i = 0; i < m; i++)
if(e[i].u 和 e[i].v 不在同一连通分量) {
把边 e[i] 加入 MST
合并 e[i].u 和 e[i].v 所在的连通分量
}
6、Huffman编码
一种可变字长编码(VLC)方式; 广泛应用于数据文件的压缩; 【前缀码】;
【构建方法】: 每次都选择根节点“频率”值最小的两棵树合并
- 给定一个具有 n 个权值{ w1 , w2 , …, wn }的结点的集合F = { T1 , T2 , ⋯ Tn }
- 初始时,设集合 A = F。
- 执行 i = 1 至 n -1 的循环,在每次循环时执行以下操作:
- 从当前集合中选取权值最小、次最小的两个结点,以这两个结点作为内部结点 bi 的左右儿子,bi 的权值为其左右儿子权值之和。
- 在集合中去除这两个权值最小、次最小的结点,并将内部结点bI 加入其中。这样,在集合A中,结点个数便减少了一个。
- 这样,在经过了n-1 次循环之后,集合A中只剩下了一个结点,这个结点就是根结点。
给定字符集C={c1,c2,...,cn},每个字符ci都有相应的频率fi
根据字符集构建结点集S={s1,s2,...,sn},每个结点si保存有字符ci和频率fi的信息
while |S| != 1 do
取出S中频率最小的两个结点x和y;
构造父节点z;
z.f = x.f + y.f;
z.c = undefined;
z.left = x;
z.right = y;
将x和y从S中移走,将z加入S;
endWhile
此时S[0]就是根节点,返回根节点
六、随机算法
- 数值随机化算法—常用于数值问题的求解,往往得到近似解。
- 蒙特卡洛算法—用于求问题的准确解
- 拉斯维加斯算法—不会得到不正确的解。
- 舍伍德算法—总能求得问题的一个解,且求得的解总是正确的。
1、数值随机化算法
。。。
2、拉斯维加斯算法
在少数应用中,可能出现求不出解的情况
但一旦找到一个解,这个解一定是正确的
在求不出解时,需再次调用算法进行计算, 直到获得解为止
对于此类算法,主要是分析算法的时间复杂度的期望值,以及调用一次产生失败 (求不出解)的概率
3、蒙特卡罗算法
- 通常不能保证计算出来的结果总是正确的, 一般只能断定所给解的正确性不小于p ( 1/2<p<1)
- 通过算法的反复执行(即以增大算法的执 行时间为代价),能够使发生错误的概率小到可以忽略的程度
- 由于每次执行的算法是独立的,故k次执 行均发生错误的概率为(1-p)^k
4、舍伍德算法
当一个确定性算法在最坏情况和平均情况下差别较大时可在这个确定性算法中引入随机性将之改造成一个舍伍德算法;引入随机性不是为了消除最坏,而是为了减少最坏和特定实例的关联性。
Testing String Equality
Monte Carlo算法
【指纹】令I(x)是x的编码,取Ip(x) ≡ I(x) (mod p)作 为x的指纹,p是一个小于M的素数
首先由A发一个x的长度给B,若长度不等,则x≠y
若长度相等,则采用“取指纹”的方法:
- A对x进行处理,取出x的“指纹”,然后将x的“指 纹”发给B
- 由B检查x的“指纹”是否等于y 的“指纹”
- 若取k次“指纹”(每次取法不同),每次两者结 果均相同,则认为x与y是相等的
- 随着k的增大,误判率可趋于0
Pattern Matching
步骤:
- 记X(j)=xj xj+1…xj+m-1(从X的第j位开始、 长度与Y一样的子串) ;
- 随机取一个小于M的素数p,置j←1
- 从起始位置j=1开始到j=n-m+1,不去逐一 比较X(j)与Y,而仅逐一比较X(j)的指纹 Ip(X(j))与Y的指纹Ip(Y) ;( 由于Ip(X(j+1))可以很方便地根据Ip (X(j))计算出来,故算法可以很快完成 )
本算法可以转成Las Vegas算法: 当Ip(Y)=Ip(X(j))时,不直接return j,而去 比较Y和X(j)
Random Sampling问题
【问题描述】设给定n个元素,从n个数中随机地选取m个数(m≤n),m个数指互不相同的
Las Vegas算法:
- 可以用一个长为n的 布尔数组B 来标识 i 是否被选中
- 初始时均表为“未选中”
- 然后随机产生〔1,n〕之间的一个整数 i ,若B[i]为“未选中”,则将i加入被选中队列,同时把B[i]标 识为“已选中”
- 反复执行直到m个不同的数全部被选出为止
上述算法存在的问题 ①
- 当n和m很接近时,产生最后几个随机数的时间可能 很长(有95%以上的可能性是已选中的数)
- 改进方法:当m>n/2时,先去生成(n-m)(<n/2)个随机 数,然后再取剩下的m个数作为选出的数
主元素问题
【主元素】设T[1:n]是一个含有n个元素的数组。当 {i|T[i]=x}|>n/2时,称元素x是数组T的主元素
Monte Carlo算法
// 判断是否 含有主元素
public static boolean majority(int[]t, int n) {
// 判定主元素的蒙特卡罗算法 rnd = new Random();
int i=rnd.random(n)+1; int x=t[i];
// 随机选择数组元素
int k=0;
for (int j=1;j<=n;j++)
if (t[j]==x) k++;
return (k>n/2); // k>n/2 时t含有主元素
}
多次重复调用,计算时间与调用次数有关
素数测试问题
蒙特卡罗
(1) 费马小定理: 满足Fermat条件的数未必全是素数
当  为素数,则有
为素数,则有  (0<a<p) , 必要条件
(0<a<p) , 必要条件
若 a^(p-1) != 1 (mod p),则 p 必为合数
(2)二次探测:如果  是一个素数,
是一个素数, , 则方程
, 则方程  的解为
的解为  或
或 
利用二次探测定理,可以在基于Fermat条件判断时,增加二次探测,若违背二次探测条件,则可得出不是素数的结论。
n后问题
Las Vegas算法
棋盘上相继的各行中随机地放置皇后,并注意使新放置的皇后与已放置的皇后互不攻击,直至n个皇后均已相容地放置好,或已没有下一个皇后的可 放置位置时为止
n后问题的Las Vegas算法思路:
各行随机放置皇后,使新放的与已有的互不攻击, until ( n皇后放好 || 无可供下一皇后放置的位置)
七、回溯法 & 分支限界法
(一) 回溯法
1、图的基本知识
邻接表
邻接矩阵
广度优先搜索(BFS)
深度优先搜索(DFS)
2、回溯法知识
回溯法的基本做法是搜索,它是一种可以**【避免不必要搜索】的 【穷举式搜索法】**
回溯法适用于求解一些**【组合数较大】**的问题
1) 回溯法的基本思想
回溯法在问题的解空间树中,按深度优先策略,从根结点出发搜索解空间树.
2) 问题的解空间
问题的解空间一般用解空间树的方式组织
- 树的根节点位于第一层,表示搜索的初始状态
- 第二层的节点表示对解向量的第一个分量做出选择后到达的状态
- 第一层到第二层的边上标出对第一个分量选择的结果
- 依此类推,从树的根节点到叶子节点的路径就构成 了解空间的一个可能解
生成问题状态的说明
- 扩展结点 —— 一个正在产生儿子的结点称为扩展结点
- 活结点 —— 一个自身已生成但其儿子还没有全部生成的节点称做活结点
- 死结点 —— 一个所有儿子已经产生的结点称做死结点
生成问题状态的基本方法——DFS
深度优先的问题状态生成法。
如果对一个扩展结点R,一旦产生了它的一个儿子C, 就把C当做新的扩展结点。在完成对子树C(以C为 根的子树)的穷尽搜索之后,将R重新变成扩展结 点,继续生成R的下一个儿子(如果存在)
生成问题状态的基本方法——回溯法
回溯法:为了避免生成那些不可能产生最优解的问题状态,要不断地利用限界函数 (bounding function)来“处死”那些实际上 不可能产生所需解的活结点,从而减少问题的计算量
具有**【限界函数的深度优先生成法】**称为回溯 法
3)回溯法的基本思想
(1) 针对所给问题,定义问题的解空间
- 复杂问题常有很多可能解,这些解构成解空间
- 确定正确的解空间很重
(2) 确定易于搜索的解空间结构
(3) 以深度优先方式搜索解空间,并在搜索过程中用剪枝函数避免无效搜索
【常用剪枝函数】
-
用约束函数在扩展结点处剪去不满足约束 的子树
-
用限界函数剪去得不到最优解 的子树
在搜索至树上任意一点时,先判断该节点 对应部分解是否满足约束条件,或是否超 出目标函数的界 判断该节点是否包含问题的(最优)解。
• 不包含,则跳过对以该节点为根的子树的搜索, 剪枝(pruning)
• 包含,则进入以该节点为根的子树,继续按 深度优先搜索
【回溯法实现方式】
-
递归回溯 — 回溯法对解空间作深度优先搜索,因此, 在一般情况下用递归方法实现回溯法
-
迭代回溯 — 用树的非递归深度优先遍历算法,可将回溯法表示为一个非递归迭代过程
【子集树和排列树】
-
子集树 - O(2^n):当所给问题是从n个元素的集合S 中找出S满足某种性质的子集时,相应的解空间树
-
排列树 - O(n!) :当所给问题是确定n个元素满足某种性质的排列时,相应的解空间树称为 排列树
3、装载问题
1)【问题描述】: 有一批共有 n 个集装箱要装上两艘载重量分别为 c1 和 c2 的轮船,其中集装箱 i 的重量为 w[i], 且重量之和小于(c1 + c2)。装载问题要求确定是否存在一个合理的装载方案可将这 n 个集装箱装上这两艘轮船。如果有,找出一种装载方案。
2)【问题分析】
容易去证明:如果一个装载问题有解,则采用下面的策略可以得到最优装载方案:
①首先将第一艘轮船尽可能装满;② 然后将剩余的集装箱装在第二艘轮船上。
3)【算法实现】
// https://www.cnblogs.com/xymqx/p/3724356.html
void Loading<Type>::Backtrack(int i)
{
if(i>n) // 回溯到叶节点
{
if(cw>bestw)
bestw = cw;
return;
}
r-=w[i]; //计算剩余(未考察)的集装箱的重量,减去当前考察过的对象的重量
if(cw+w[i] <= c)
{
cw += w[i];
Backtrack(i+1);
cw -= w[i];
}
Backtrack(i+1);
r+=w[i]; //递归回退返回上一层时,记得修改r的当前值,如果得不到最优解,再取消当前考察的集装箱,标记为未选,因此剩余容量要再加上当前集装箱重量
}
// ============================================================================//
// 加入剪枝
void Loading<Type>::Backtrack(int i)
{ //搜索第i层结点
if(i>n) //到达叶子结点
{
if(cw>bestw) {
for(j=1;j<=n;j++)
bestx[j] = x[j]; //记录最优路径
bestw = cw; //若cw>bestw,更新bestw=cw
}
return;
} //搜索子树
r-=w[i]; //计算剩余(未考虑过)集装箱的重量,减去当前考虑过的集装箱重量
if(cw+w[i] <= c) //搜索左子树
{
x[i] =1; //左子树1,右子树0
cw += w[i]; //进入子树,则+
Backtrack(i+1);
cw -= w[i]; //表示从Backtrack(i+1)里出来,则复原cw,所以前面+,这里则-,恢复原状
}
// r 剩余集装箱的重量
if(cw+r > bestw) //搜索右子树——————剪枝函数
{
x[i] = 0;
Backtrack(i+1);
}
r+=w[i]; //递归返回上一层时,记得修改r的值,如果取不到最优解,再取消当前考虑的集装箱,标记为未选,因此剩余容量要再加上当前集装箱重量
}
4、批处理作业调度
1)问题描述
每一个作业 Ji 都有两项任务分别在2台机器上完成。每个作业必须先由机器1处理,然后再由机器2处理。作业 Ji 需要机器 j 的处理时间为 tji。对于一个确定的作业调度,设 Fji 是作业 i 在机器 j 上完成处理时间。则所有作业在机器2上完成处理时间和 f=F2i ,称为该作业调度的完成时间和
【参考网址】
https://blog.youkuaiyun.com/m0_46308522/article/details/109425775
https://www.cnblogs.com/wkfvawl/p/11765576.html
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-BYznKKyn-1648911071052)(C:\Users\Weller.Y\AppData\Roaming\Typora\typora-user-images\1638880968987.png)]
int n; //作业数
int M[100][100]; //M[i][j]表示第i个作业在机器j上需要处理的时间
int x[100]; //x[i]表示第i个处理的作业为x[i]
int bestx[100]; //x[i]的最优值
int f1; //作业在机器1上完成处理的时间
int f2[100]; //f2[i]表示第i个作业在机器2上完成处理的时间
int f; //用于记录 前i个作业在机器2上完成处理的时间和
int bestf; //f的最优值
void Backtrack(int i)
{
if(i>n) //每到达一个叶子结点,一定是产生了一个最优解,因此要更新之前最优解的值
{
if(f<bestf) //更新最优解
{
for(int j=1;j<=n;j++)
bestx[j]=x[j]; //更新最优调度序列
bestf=f; //更新最优目标值
}
}
else {
for(int j=i;j<=n;j++) //控制展开i-1层结点的各个分支。例如当i=1时,表示在整棵排列树的根结点处,刚要开始探索结点,这时可以展开的分支有1、2、3……
{
f1 += M[x[j]][1]; //计算第i层(个)作业在机器1上的完成处理的时间
//若第(i-1)个作业在机器2上的完成处理的时间 > 第i个作业在机器1上的完成处理的时间,那么第i个作业想进入机器2,就要等第(i-1)个作业在机器2上完成后
if(f2[i-1] > f1)
f2[i] = f2[i-1] + M[x[j]][2]; //保存当前作业在机器2的完成时间
else //否则,第i个作业可以在机器1上完成处理后直接进入机器2。
f2[i] = f1 + M[x[j]][2]];
f += f2[i]; //在机器2上的完成时间和
if(f < bestf) //截止到这,已经得到一个前i个作业在机器2上完成处理的时间和f,如果f比之前记录的前i个作业在机器2上的完成处理的时间和的最优值bestf都要小,就可以生成第i层结点的孩子结点,继续探索下一层
{
Swap(x[i],x[j]); //把处于同一层的并且使f更小的那个结点拿过来,放到正在探索的这个结点处(这里结合排列数的图可以更好地理解)
Backtrack(i+1); //继续探索以第i层结点为根结点的子树
Swap(x[i],x[j]); //探索完要回溯时,只要做探索前的反“动作”就可以了
}
f -= f2[i]; //探索完要回溯时,只要做探索前的反“动作”就可以了
f1 -= M[x[j]][1]; //探索完要回溯时,只要做探索前的反“动作”就可以了
}
}
}
5、符号三角形问题
用n元组x[1:n]表示符号三角形的第一行的n个符号,当x[i]等于1时,表示符号三角形的第一行的第i个符号为“+”;当x[i]等于0时,表示符号三角形的第一行的第i个符号为“-”;1<=i<=n。由于x[i]是2值的。所以在用回溯法解符号三角形问题时,可以用一棵完全二叉树来表示其解空间。在符号三角形的第一行的前i个符号x[1:i]确定后,就确定了一个有i*(i+1)/2个符号组成的符号三角形。(i*(i+1)/2来自首项为1、公差为1的等差数列的求和公式)
下一步确定x[i+1]的值后,只要在前面已确定的符号三角形的右边加一条边,就可以拓展为x[1:i+1]所对应的符号三角形。最终由x[1:n]所确定的符号三角形包含的“+”个数与“-”同为n(n+1)/4(n(n+1)/2的一半,也就是一半的符号)。因此,在回溯可将“+”、“-”个数均 不超过n(n+1)/4为约束条件。同时,对于给定的n当n(n+1)/2为奇数时,显然不存在“+”和“-”个数相同的符号三角形。 计算时间为 O(n2^n)。
可行性约束函数:当前符号三角形所包含 的“+”个数与“-”个数均不超过n***(n+1)/4
无解的判断**:n*(n+1)/2为奇数
https://www.cnblogs.com/wkfvawl/p/11766662.html
public static int n, half, count;// 第一行的符号个数n,当前“+”个数count,
public static int[][] p;// 符号三角形矩阵
public static long sum;// 符合条件的符号三角形个数
public static void backtrack(int t) {
// 剪枝, 判断"+"或"-"是否都超过了一半
if ((count > half) || (t * (t - 1) / 2 - count > half))
return;// 若符号统计未超过半数,并且另一种符号也未超过半数
if (t > n) { //可行性约束
sum++;
} //当t>n时,算法搜索至叶节点,得新的“+”与“—”个数相同的符号三角形,当前已找到的符号三角形数sum增1.
else {
for (int i = 0; i <= 1; i++) {
p[1][t] = i;
count += i;
for (int j = 2; j <= t; j++) {
//这里可能有一些难推导,第t列的这个符号只能影响下面几行的t列之前的符号
//如果当前行为k,下面的行数为j,则t最多可以影响到的列数为t-(j-k)即为t-j+k
//在一行中即为t-j+1
/*
if (p[j - 1][t - j + 1] == p[j - 1][t - j + 2]) {
p[j][t - j + 1] = 1;
// 2个同号下面都是“+”
}
else {
p[j][t - j + 1] = 0;
// 2个异号下面都是“-”
}
*/
//用0,1表示的一个好处是可以使用异或运算,来计算下层结果
p[j][t-j+1] = p[j-1][t-j+1] ^ p[j-1][t-j+2];
count += p[j][t - j + 1];
}
backtrack(t + 1); // 回溯
for (int j = 2; j <= t; j++) {
// 回溯时取消上一次的赋值
count -= p[j][t - j + 1];
}
count -= i;
}
}
}
6、n后问题
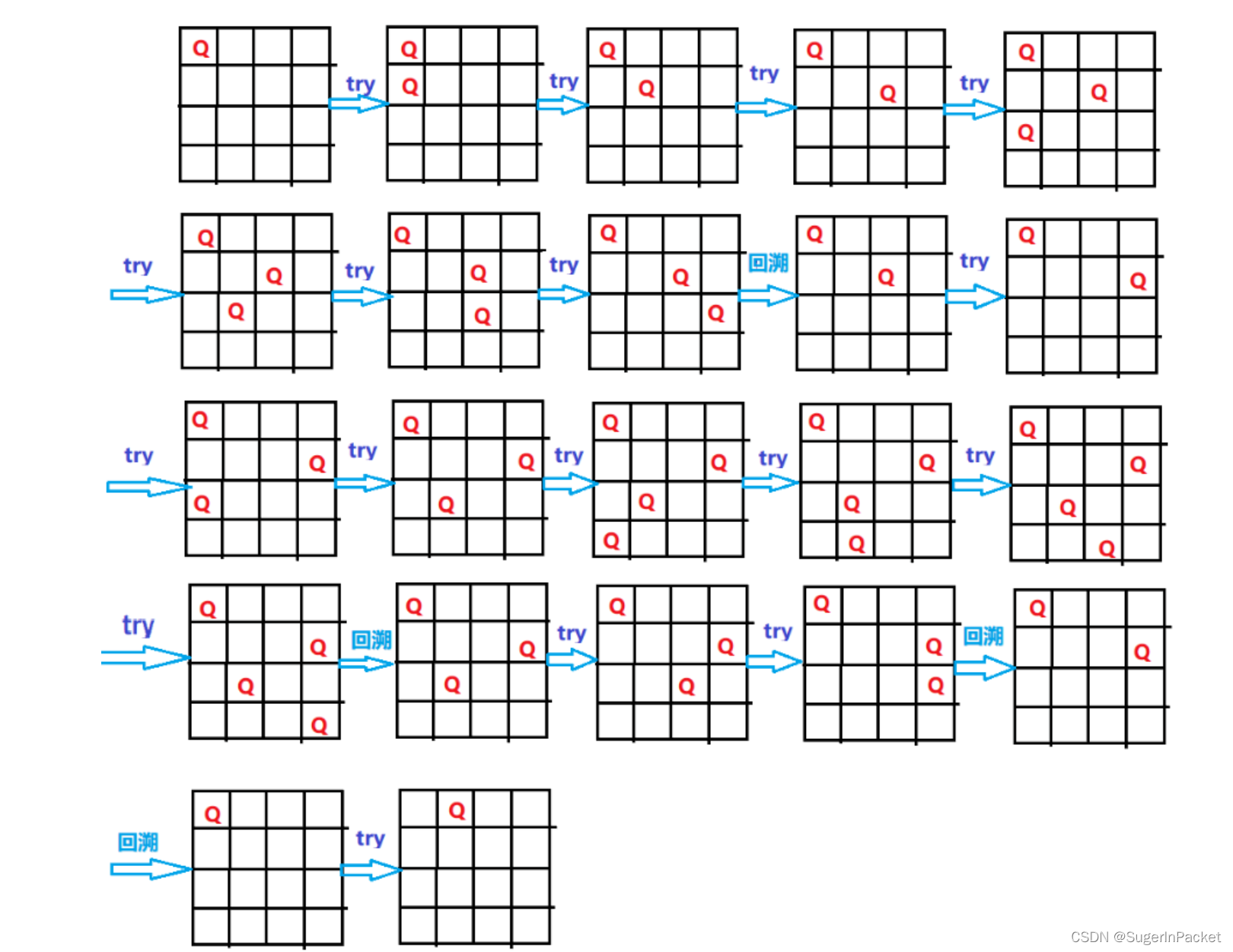
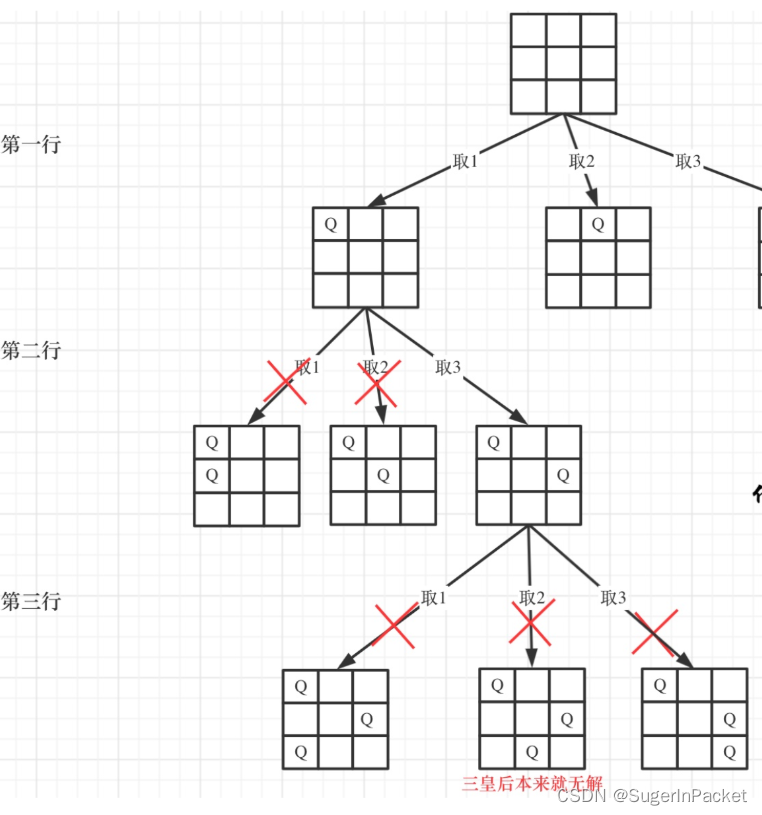
1)问题描述
在n*n格的棋盘上防止彼此不受攻击的n个皇后,按照国际象棋的规则,皇后可以攻击与之处在同一行、同一列 或同一斜线上的棋子。n后问题等价于,在n *n 的棋盘上防止n个皇后,任何两个不能满足攻击条件。
2)问题分析
https://cloud.tencent.com/developer/article/1424758
【核心代码】
// n 为输入的棋盘大小
// row 是当前递归到棋牌的第几行了
void backtracking(int n, int row, vector<string>& chessboard) {
if (row == n) {
result.push_back(chessboard);
return;
}
for (int col = 0; col < n; col++) {
if (isValid(row, col, chessboard, n)) { // 验证合法就可以放
chessboard[row][col] = 'Q'; // 放置皇后
backtracking(n, row + 1, chessboard);
chessboard[row][col] = '.'; // 回溯,撤销皇后
}
}
}
// 检查皇后位置是否相容
bool isValid(int row, int col, vector<string>& chessboard, int n) {
int count = 0;
// 检查列
for (int i = 0; i < row; i++) // 这是一个剪枝
if (chessboard[i][col] == 'Q') return false;
// 检查 45度角是否有皇后
for (int i = row - 1, j = col - 1; i >=0 && j >= 0; i--, j--)
if (chessboard[i][j] == 'Q') return false;
// 检查 135度角是否有皇后
for(int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++)
if (chessboard[i][j] == 'Q') return false;
return true;
}
7、0-1背包问题
解空间:子集树
1)问题描述
给定 n 种物品和一背包。物品 i 的重量是 wi > 0,其价值为 vi > 0,背包的容量为 c 。问应如何选择装入背包中的物品,使得装入背包中物品的总价值最大? (要求使用回溯法)
//用于记录是否存放当前地物体
int inOut[n];
//保存最多的价值
int value_max;
//定义背包的总共的重量的
int bagVolume = c;
/*
描述:背包问题的约束条件,当传入对应的序号,就去判定是否要放对应的物品
参数:放入包中物体的序号
返回:当前物体总重量和背包容量的关系
true:表示没有超重
false:表示超重
原理:判定当前的物品的总重量,是不是小于物体的实际重量
*/
bool bagConstraint(int m, int weight[]) {
//一直遍历m层之前的所有物体,求出其对应的重量
int allweight = 0;
for (int i = 0; i <= m; ++i)
//计算出总共的重量的
allweight += inOut[i] * weight[i];
//比较当前的物体总重量和背包的总重量关系
return allweight <= bagVolume;
}
/*
描述:深度优先搜索的函数,递归函数
参数:m:是要装入背包的物品的数量
weight:是背包中各个物品的重量
value:是背包中各个物品的价值
返回:最终返回的是最大的价值
问题:
*/
void back_tracing_0-1bag(int m, int n, int weight[], int valueAll[]) {
//首先确定终止条件,那就比较最大值
if (m == n) {
int sum = 0;
for (int i = 0; i < m; ++i)
sum += valueAll[i] * inOut[i];
//比较最大值
if (sum > value_max) value = sum;
}
else {
//没有到达终止条件,继续向下进行递归
for (int i = 0; i < 2; ++i) {
inOut[m] = i;
//判定是否满足对应约束条件
if (bagConstraint(m, weight))
//满足约束条件,继续向下进行递归的
back_tracing_0-1bag(m + 1, n, weight, valueAll);
}
}
}
8、图的m着色问题
1.将数组color[n]初始化为0;
2.k=1;
3.while (k>=1)
3.1 依次考察每一种颜色,若顶点k的着色与其他顶点的着色不发生冲突,则转步骤3.2;否则,搜索下一个颜色;
3.2 若顶点已全部着色,则输出数组color[n],返回;
3.3 否则, 3.3.1 若顶点k是一个合法着色,则k=k+1,转步骤3 处理下一个顶点;
3.3.2 否则,重置顶点k的着色情况,k=k-1,转步 骤3回溯;
图的m着色问题应用举例
三着色问题:机场停机位分配是指根据航班和机型等属性,为每个航班指定停机位。要满足下列约束:
1) 各航班须被分配,且仅能被分配一个停机位; 2) 同一时刻同一停机位不可分配1个以上的航班;
3) 应满足航站衔接以及过站时间衔接要求; 4) 机位与使用机位航班应相互匹配。
9、旅行售货员问题
1) 问题描述
某售货员要到若干城市去推销商品,已知各城市之间的路程,他要选定一条从驻地出发,经过每个城市一遍,最后回到住地的路线,使总的路程最短。
2) 问题分析
解空间树 —— 排列树
10、圆排列问题
这个问题的解空间应该是一棵排列树。因为圆就是按照一定的顺序排在矩形框中的,这里面我们将圆的半径进行排序,从而代表圆排序。其中a=[r1,r2,…,rn]就是我们的序列。
// https://blog.youkuaiyun.com/weixin_44755413/article/details/106095725
// CirclePerm(n,a)返回找到的最小圆排列长度。
// 初始时,数组a是输入的n个圆的半径,计算结束后返回相应于最优解的圆排列。
// Center计算当前所选择的圆在当前圆排列中圆心的横坐标,
// Compute计算当前圆排列的长度,
// 变量min记录当前最小圆排列的长度,数组r表示当前圆排列,
// 数组x则记录当前圆排列中各圆的圆心横坐标。
// 算法中约定在当前圆排列中排在第一个的圆的圆心横坐标为0.
class Circle
{
friend float CirclePerm(int,float *);
private:
float Center(int t);//计算当前所选择圆的圆心横坐标
void Compute(void);
void Backtrack(int t);
float min,//当前最优值
*x,//当前圆排列圆心横坐标
*r;//当前圆排列(可理解为半径排列)
int n;//待排列圆的个数
float Circle::Center(int t)
{
float valuex,temp = 0;
//之所以从1-t判断是因为防止第t个圆和第t-1个圆不相切
for(int j = 1;j < t;j++)
{
valuex = x[j] + sqrt(r[t] * r[j]);
if(valuex > temp)
temp = valuex;
}
return temp;
}
void Circle::Compute(void)
{
float low = 0,high = 0;
for(int i = 1;i <=n;i++)
{
if(x[i] - r[t] < low) low = x[i] - r[i];
if(x[i] + r[i] > high) high = x[i] + r[i];
}
if(high - low < min) min = high - low;
}
void Circle::Backtrack(int t)
{
if(t > n)
//到达叶子节点,我们计算high与low的差距
Compute();
else
{
//排列树解空间
for(int j = 1;j <= t;j++)
{
//圆的排列其实就是就是半径的排列,因为相同半径的圆是相同的
//交换半径顺序,可以进一步优化,如果半径相等不交换
//镜像序列只算一次,例如1,2,3和3,2,1
swap(r[t],r[j]);
if(Center(t)+r[1]+r[t] < min)//下界约束,我们取第一个圆的圆心为原点,所以计算距离的时候要加上r[1]和r[t]
{
x[t] = Center(t);
Backtrack(t+1;)
}
swap(r[t],r[j]);
}
}
}
float CirclePerm(int n,float *a)
{
Circle X;
X.n = n;
X.r = a;
X.min = 100000;
float *x = new float [n+1];//圆的中心坐标排列
X.x = x;
X.Backtrack(1);
delete[] x;
return X.min;
}
};
(二) 分支限界法
1、分枝限界法和回溯法
相同点:是在问题的【解空间树】上搜索问题解的算法
不同点:
- 求解目标不同:回溯法的求解目标是找出解空间树中满 足约束条件的所有解,而分枝限界法的求解目标则是找出满足约束条件的一个解,或是在满足约束条件的解中找出在某种意义下的最优解
- 搜索方式的不同:回溯法以深度优先的方式搜索解 空间树,而分枝限界法以广度优先或以最小耗费优先的方式搜索解空间树
2、分枝限界法的基本思想
https://blog.youkuaiyun.com/u010089444/article/details/74331907
https://blog.youkuaiyun.com/weixin_44712386/article/details/105532881
分支 —— 使用广度优先策略,依次生成扩展结点的所有分支。
限界 —— 在结点扩展过程中,计算结点的上界,搜索的同时剪掉某些分支。
分支限界法就是把问题的可行解展开,再由各个分支寻找最佳解。
与回溯法类似,分支限界法也是在解空间树中搜索得到解;
不同的是,分支限界法会生成所有扩展结点,并舍弃不可能通向最优解的结点,然后根据广度优先/最小耗费优先,从活结点中选择一个作为扩展结点,使搜索向解空间上有最优解的分支推进
分枝限界法常以广度优先或以最小耗费 (最大效益)优先的方式搜索问题的解空间树
- 在分枝限界法中,每一个活结点只有一次机会成为【扩展结点】。活结点一旦成为扩展结点,就一次性产生其所有儿子结点。在这些儿子结点中,导致不可行解或导致非最优解的儿子结点被舍弃,其余儿子结点被加入活结点表中
- 此后,从活结点表中取下一结点成为当前扩展结点, 并重复上述结点扩展过程。这个过程一直持续到找到所需的解或活结点表为空时为止
3、常见的两种分枝限界法
队列式(FIFO)分枝限界法
按照队列先进先出(FIFO)原则选取下一个节点为 扩展节点
优先队列式分枝限界法
- 按照优先队列中规定的优先级选取优先级最高的节点成为当前扩展节点
- 应用优先队列式分枝限界法求解具体问题时,应该根据具体问题的特点确定选用**最大优先队列(最小优先队列)**表示解空间的活结点表
4、装载问题
有一批共n个集装箱要装上2艘载重量分别 为c1和c2的轮船,其中集装箱i的重量为wi, 且∑ Wi ≤ c1 + c2 ;
装载问题要求确定是否有一个合理的装载 方案可将这些集装箱装上这2艘轮船。如果有,找出一种装载方案
【算法解释】https://blog.youkuaiyun.com/qq_44766883/article/details/106904355
【详细步骤解释】https://my.oschina.net/wangshengzhuang/blog/785027
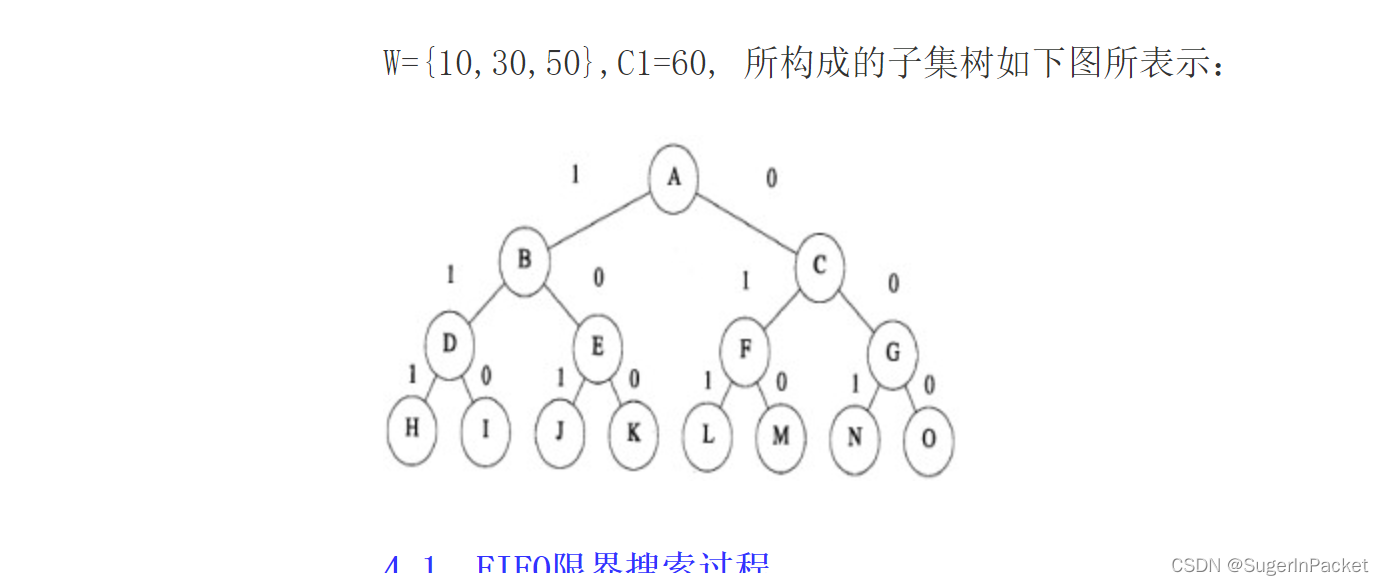
(1) 队列式 分支限界法

(2)优先队列式 分支限界法

5、0-1背包问题
6、旅行售货员问题
1)问题描述

给定一个n顶点网络(有向或无向),找出一个包含n个顶点且具有最小耗费 的换路。任何一个包含网络所有顶点的换路称为一个旅行。**旅行商问题(Traveling Salesman Problem,TSP)**是要寻找一条耗费最少的旅行。
2)算法描述
https://blog.youkuaiyun.com/qq_44766883/article/details/106992785
- 要找最小费用旅行售货员回路,选用
最小堆表示活结点优先队列。 - 算法开始时创建一个最小堆,用于表示活结点优先队列。
- 堆中每个结点的优先级是
子树费用的下界lcost值。 - 计算
每个顶点i的最小出边费用并用min_out[i]记录 - 如果所给的
有向图中某个顶点没有出边,则该图不可能有回路,算法结束。

八、NP 理论
P 问题是【容易解决】的问题,P类问题是多项式时间可解的
NP 问题是【容易验证】的问题,NP类问题是多项式时间可验证的
NPC问题(NP Complete):NP完全问题,所有NP问题在多项式时间内都能规约(Reducibility)到它的NP问题,即解决了此NPC问题,所有NP问题也都能得到解决。
NP-hard(NP hard):NP难问题,所有NP问题在多项式时间内都能规约(Reducibility)到它的问题,但不一定是NP问题。

归约(reduction): 归约是证明NP-hard问题的一种常用方法,通常用<=这个符号来表示。如P<=Q,这个就表示P is reducible to Q , or Q is the reduction from P or P is reduced to Q(P问题可以归约到Q问题,or可以把P归约到Q) 。这里的reduction的符号可以当成是 比较难易程度的小于等于号,意味着P至少比Q容易,或者Q至少比P难。
归约主要做的就是以下两个转化(注意两个转化都要在polynomial的时间内完成)【已知P是个NP-hard问题,证新问题Q 亦是NP-hard问题】,
1.把P的输入转化到Q的输入; 2. 把Q的输出转化到P的输出。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-CEjtKOnM-1648911071053)(C:\Users\Weller.Y\AppData\Roaming\Typora\typora-user-images\1639227159358.png)]

- 证明NP问题。这个容易,即给你一个结果,你能在polynomial的时间内验证该结果的正确性。
- 证明NP-hard问题。我们要证明一个问题是NP-hard的时候,我们通常要做的是找到一个已被证明了的NPC问题,并把这个NPC问题归约到该问题上去(即NPC<=NP-hard)。
- 证明NP-Complete问题。分以下两步:
- 第一步,证明这个问题属于NP;
- 第二步,证明这个问题是NP-hard的。

问题的多项式变换(规约)
设IA是判定问题A的任一实例,B是另一判定 问题,若存在一个从A到B的映射f满足
- ∀IA∈A ,实例IA的答案为‘Yes’ iff f(IA)(与 IA相对应 的B问题的实例)的答案为‘Yes’
- IA∈A,若IA的输入规模为n,则对应实例f(IA)的输入 规模不超过PA(n),这里PA(n)是一个与判定问题A有关 的多项式
- IA∈A ,若IA的输入规模为n,则对应实例f(IA)的输 入在多项式时间p(n)内可计算
则称问题A可多项式变换为B,记作A≤pB, (≤p亦称Karp规约)
多项式变换(规约)的作用
若A≤pB且问题B是多项式时间可判定的, 则问题A也一定是多项式时间可判定的。
要证明一个判定问题B是NP-C的:
① 证明B是多项式时间可验证的(从而B属于 NP类)
② 还要找一个NP-C问题A,证明A 可以在多项式时间里变换为B,且A的任 一实例回答为‘Yes’ iff与之对应的B的实 例回答为‘Yes’
NP-hard类问题的求解方法
- 当n不太大时,可使用 a) 动态规划法 b) 分枝限界法 c) 回溯法
- 求近似解。在误差允许的范围之内找一个 解,该近似解可以在多项式时间里得到。
- 用启发式算法求解
- 智能优化算法。常常能获得很好的结果。 但有偶然性,与最优解的误差难以给出
九、近似算法
许多具有实际意义的问题都是NP完全问题。我们不知道如何在多项式时间内求得最优解。但是,这些问题通常十分重要,我们不能因此而放弃对它们的求解。即使一个问题是NP完全的,也有其解次方法。
解决NP完全问题至少有三种方法:
1)如果实际输入数据规模较小,则用指数级运行时间的算法就能很好地解决问题;
2)对于一些能在多项式时间内解决的特殊情况,可以把它们单独列出来求解;
3)可以寻找一些能够在多项式时间内得到近似最优解(near-optimal solution)的方法(最坏情况或平均情况)。在实际应用中,近似最优解一般都能满足要求。返回近似最优解的算疫就称为近似算法(approximation algorithm)。
使用近似算法的目的: 近似算法其实是针对NP难问题的一种退让,对于许多P不等于NP的最优化问题,无法在多项式时间内找到最优解。因此,如果可以只求一个我们可以接受的解,而不是非要最优解,那么可能存在一个多项式时间的算法。
1、装箱问题(Bin Packing)
设有n个物体u1,u2,…,un,每个物体的体积不超过1。另外,有足够多的、体积为1的箱子。箱子、物体均是长方体且截面相同 ,问如何装箱,使得所用箱子数最少。
(1) First-Fit(FF)算法
- 从排在最前面的箱子开始,对每个箱子剩余的体积逐一进行检查,一旦碰到第一个能够装进当前物体的箱子时,就立即把该物体装入这个箱子。对每个物体反复执行上述程序。
- 算法的最坏时间复杂度:O(n^2)
- 用FF算法不能保证所获得的解是最优解
(2) Next-Fit(NF)算法
- 先把第一个空箱置为当前箱。然后依次把物品 u1,u2,…,un按下列方式装箱:若当前所指的箱子里放得下ui,则把ui放入箱中;若放不下, 则把ui放入下一 个空箱,把当前指针指向(放ui的)该箱
- 算法的最坏时间复杂度:O(n)
(3) Best-Fit(BF)算法
- FF算法的修改:在已装有物品的箱子中,找一个既能放下ui、又使得其剩余空间最小的箱子来放ui
- 表面上看起来该算法要比FF法更能充分利用空间, 但实际上,Johnson等人证明了BF法在最坏情况下 的性能,本质上与FF法相同
(4)FFD(First-Fit Decreasing)算法
先将所有物品从大到小排序,然后再使用FF法
2、顶点覆盖问题
- 无向图G=(V,E)的顶点覆盖是它的顶点集V的一个子集V’⊆V,使得若(u,v)是G的一条边,则v∈V’或 u∈V’
- 顶点覆盖V’的大小是它所包含的顶点个数|V’|
- 顶点覆盖问题就是要求在一个给定的无向图中,找出一个具有最小规模的顶点覆盖,使得所有边都至少与点集中的一个点接触。
VertexSet approxVertexCover ( Graph g ) {
cset = 空集 ; // Cset用来存储顶点覆盖中的各顶点
e1 = g.e ;
while (e1 != 空集) {
从e1中任取一条边(u,v) ;
cset = cset∪{u,v} ;
从e1中删去与u和v相关联的所有边 ;
}
return c;
}
3、旅行商问题
旅行商问题(TSP)简单描述
- 给定一个完全无向图G=(V,E),其每一边(u,v)∈E 有一非负整数代价c(u,v)
- 要找出G中具有最小代价的哈密尔顿回路( 从某个顶点出发 , 将所有的顶点都走一遍, 并且每个顶点只能经过一次, 经过所有顶点的 圈 称为 哈密顿圈 , 经过所有顶点的 道路 称为 哈密顿道路 NPC )
TSP的特殊性质
- 代价函数c往往具有三角不等式性质,即对任意的3 个顶点u,v,w∈V,有:c(u,w)≤c(u,v)+c(v,w)
- 当图G中的顶点就是平面上的点,任意2顶点间的代价就是这2点间的欧氏距离时,代价函数c就具有三角不等式性质
void approxTSP (Graph g) {
(1)选择g的任一顶点r;
(2)用Prim算法找出带权图g的一棵以r为根的最小生成树T;
(3)前序遍历树T得到的顶点表L;
(4)将r加到表L的末尾,按表L中顶点次序组成回路H,作为计算结果返回;
}
法:
1)如果实际输入数据规模较小,则用指数级运行时间的算法就能很好地解决问题;
2)对于一些能在多项式时间内解决的特殊情况,可以把它们单独列出来求解;
3)可以寻找一些能够在多项式时间内得到近似最优解(near-optimal solution)的方法(最坏情况或平均情况)。在实际应用中,近似最优解一般都能满足要求。返回近似最优解的算疫就称为近似算法(approximation algorithm)。
使用近似算法的目的: 近似算法其实是针对NP难问题的一种退让,对于许多P不等于NP的最优化问题,无法在多项式时间内找到最优解。因此,如果可以只求一个我们可以接受的解,而不是非要最优解,那么可能存在一个多项式时间的算法。
1、装箱问题(Bin Packing)
设有n个物体u1,u2,…,un,每个物体的体积不超过1。另外,有足够多的、体积为1的箱子。箱子、物体均是长方体且截面相同 ,问如何装箱,使得所用箱子数最少。
(1) First-Fit(FF)算法
- 从排在最前面的箱子开始,对每个箱子剩余的体积逐一进行检查,一旦碰到第一个能够装进当前物体的箱子时,就立即把该物体装入这个箱子。对每个物体反复执行上述程序。
- 算法的最坏时间复杂度:O(n^2)
- 用FF算法不能保证所获得的解是最优解
(2) Next-Fit(NF)算法
- 先把第一个空箱置为当前箱。然后依次把物品 u1,u2,…,un按下列方式装箱:若当前所指的箱子里放得下ui,则把ui放入箱中;若放不下, 则把ui放入下一 个空箱,把当前指针指向(放ui的)该箱
- 算法的最坏时间复杂度:O(n)
(3) Best-Fit(BF)算法
- FF算法的修改:在已装有物品的箱子中,找一个既能放下ui、又使得其剩余空间最小的箱子来放ui
- 表面上看起来该算法要比FF法更能充分利用空间, 但实际上,Johnson等人证明了BF法在最坏情况下 的性能,本质上与FF法相同
(4)FFD(First-Fit Decreasing)算法
先将所有物品从大到小排序,然后再使用FF法
2、顶点覆盖问题
- 无向图G=(V,E)的顶点覆盖是它的顶点集V的一个子集V’⊆V,使得若(u,v)是G的一条边,则v∈V’或 u∈V’
- 顶点覆盖V’的大小是它所包含的顶点个数|V’|
- 顶点覆盖问题就是要求在一个给定的无向图中,找出一个具有最小规模的顶点覆盖,使得所有边都至少与点集中的一个点接触。
VertexSet approxVertexCover ( Graph g ) {
cset = 空集 ; // Cset用来存储顶点覆盖中的各顶点
e1 = g.e ;
while (e1 != 空集) {
从e1中任取一条边(u,v) ;
cset = cset∪{u,v} ;
从e1中删去与u和v相关联的所有边 ;
}
return c;
}
3、旅行商问题
旅行商问题(TSP)简单描述
- 给定一个完全无向图G=(V,E),其每一边(u,v)∈E 有一非负整数代价c(u,v)
- 要找出G中具有最小代价的哈密尔顿回路( 从某个顶点出发 , 将所有的顶点都走一遍, 并且每个顶点只能经过一次, 经过所有顶点的 圈 称为 哈密顿圈 , 经过所有顶点的 道路 称为 哈密顿道路 NPC )
TSP的特殊性质
- 代价函数c往往具有三角不等式性质,即对任意的3 个顶点u,v,w∈V,有:c(u,w)≤c(u,v)+c(v,w)
- 当图G中的顶点就是平面上的点,任意2顶点间的代价就是这2点间的欧氏距离时,代价函数c就具有三角不等式性质
void approxTSP (Graph g) {
(1)选择g的任一顶点r;
(2)用Prim算法找出带权图g的一棵以r为根的最小生成树T;
(3)前序遍历树T得到的顶点表L;
(4)将r加到表L的末尾,按表L中顶点次序组成回路H,作为计算结果返回;
}





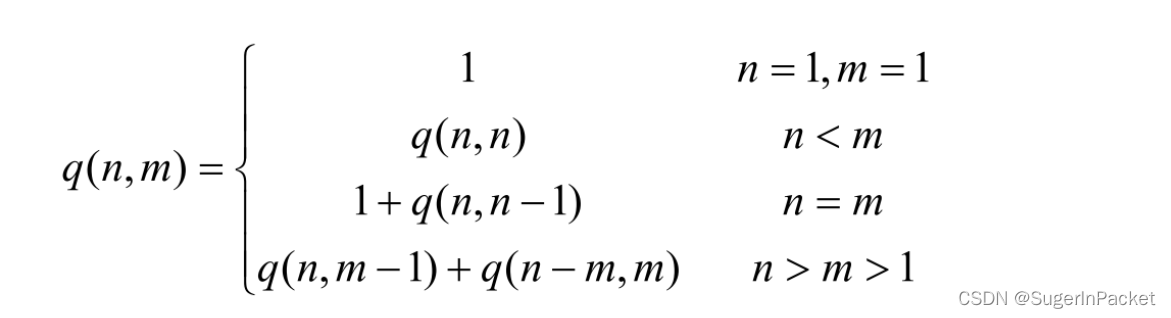
















 975
975

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








