【623. 在二叉树中增加一行】

来源：力扣（LeetCode）

描述：

给定一个二叉树的根 root 和两个整数 val 和 depth ，在给定的深度 depth 处添加一个值为 val 的节点行。

注意，根节点 root 位于深度 1 。

加法规则如下:

• 给定整数 depth，对于深度为 depth - 1 的每个非空树节点 cur ，创建两个值为 val 的树节点作为 cur 的左子树根和右子树根。
• cur 原来的左子树应该是新的左子树根的左子树。
• cur 原来的右子树应该是新的右子树根的右子树。
• 如果 depth == 1 意味着 depth - 1 根本没有深度，那么创建一个树节点，值 val 作为整个原始树的新根，而原始树就是新根的左子树。

示例 1:

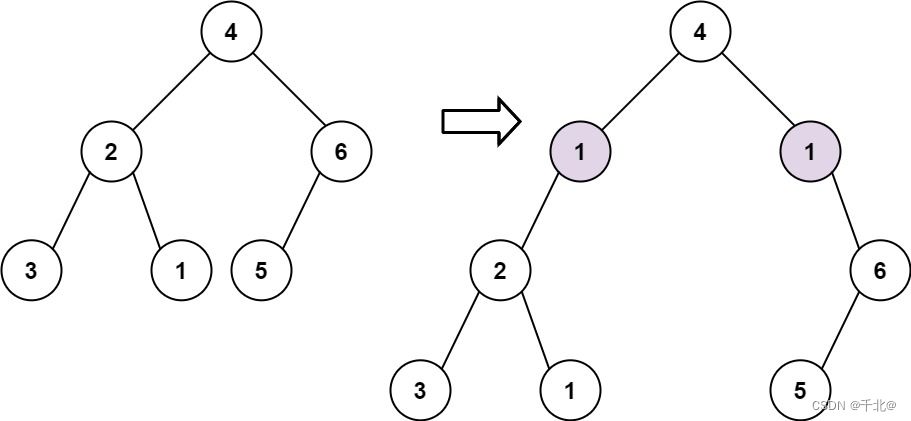
输入: root = [4,2,6,3,1,5], val = 1, depth = 2
输出: [4,1,1,2,null,null,6,3,1,5]

示例 2:

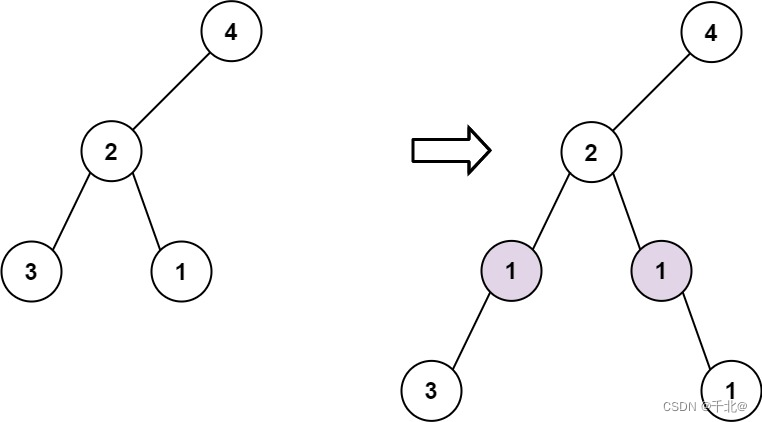
输入: root = [4,2,null,3,1], val = 1, depth = 3
输出:  [4,2,null,1,1,3,null,null,1]

提示:

• 节点数在 [1, 10⁴] 范围内
• 树的深度在 [1, 10⁴]范围内
• -100 <= Node.val <= 100
• -10⁵ <= val <= 10⁵
• 1 <= depth <= the depth of tree + 1

方法一：深度优先搜索
思路

当输入 depth 为 1 时，需要创建一个新的 root，并将原 root 作为新 root 的左子节点。当 depth 为 2 时，需要在 root 下新增两个节点 left 和 right 作为 root 的新子节点，并把原左子节点作为 left 的左子节点，把原右子节点作为right 的右子节点。当 depth 大于 2 时，需要继续递归往下层搜索，并将 depth 减去 1，直到搜索到 depth 为 2。

代码:

class Solution {
public:
    TreeNode* addOneRow(TreeNode* root, int val, int depth) {
        if (root == nullptr) {
            return nullptr;
        }
        if (depth == 1) {
            return new TreeNode(val, root, nullptr);
        }
        if (depth == 2) {
            root->left = new TreeNode(val, root->left, nullptr);
            root->right = new TreeNode(val, nullptr, root->right);
        } else {
            root->left = addOneRow(root->left, val, depth - 1);
            root->right = addOneRow(root->right, val, depth - 1);
        }
        return root;
    }
};

执行用时：12 ms, 在所有 C++ 提交中击败了93.33%的用户
内存消耗：24.2 MB, 在所有 C++ 提交中击败了75.63%的用户
复杂度分析
时间复杂度：O(n)，其中 n 为输入的树的节点数。最坏情况下，需要遍历整棵树。
空间复杂度：O(n)，递归的深度最多为 O(n)。

方法二：广度优先搜索

思路

与深度优先搜索类似，我们用广度优先搜索找到要加的一行的上一行，然后对这一行的每个节点 node，都新增两个节点 left 和 right 作为 node 的新子节点，并把原左子节点作为 left 的左子节点，把原右子节点作为 right 的右子节点。

代码:

class Solution {
public:
    TreeNode* addOneRow(TreeNode* root, int val, int depth) {
        if (depth == 1) {
            return new TreeNode(val, root, nullptr);
        }
        vector<TreeNode *> curLevel(1, root);
        for (int i = 1; i < depth - 1; i++) {
            vector<TreeNode *> tmpt;
            for (auto &node : curLevel) {
                if (node->left != nullptr) {
                    tmpt.emplace_back(node->left);
                }
                if (node->right != nullptr) {
                    tmpt.emplace_back(node->right);
                }
            }
            curLevel = move(tmpt);
        }
        for (auto &node : curLevel) {
            node->left = new TreeNode(val, node->left, nullptr);
            node->right = new TreeNode(val, nullptr, node->right);
        }
        return root;
    }
};

执行用时：20 ms, 在所有 C++ 提交中击败了47.59%的用户
内存消耗：24.6 MB, 在所有 C++ 提交中击败了5.06%的用户
复杂度分析
时间复杂度：O(n)，其中 n 为输入的树的节点数。最坏情况下，需要遍历整棵树。
空间复杂度：O(n)，数组空间开销最多为 O(n)。
author：LeetCode-Solution