python基础教学day16--树与二叉树_python二叉树中的度-优快云博客

本文深入讲解二叉树的基础概念、不同类型的二叉树及其性质、遍历方法、二叉排序树及平衡二叉树等内容。文章通过代码示例介绍了如何实现二叉树的基本操作。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一.树

1. 树是一种抽象数据类型或是实作这种抽象数据类型的数据结构,用来模拟具有树状结构性质的数据集合.
2. 它是由n(n>=1)个有限节点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵
倒挂的树,也就是说它是根朝上,而叶朝下的。它具有以下的特点:

每一个节点有零个或者多个子节点
没有父节点的节点称为根结点
每一个非根节点有且只有一个父节点
除了根节点外,每一个子节点可以分为多个不相交的子树;

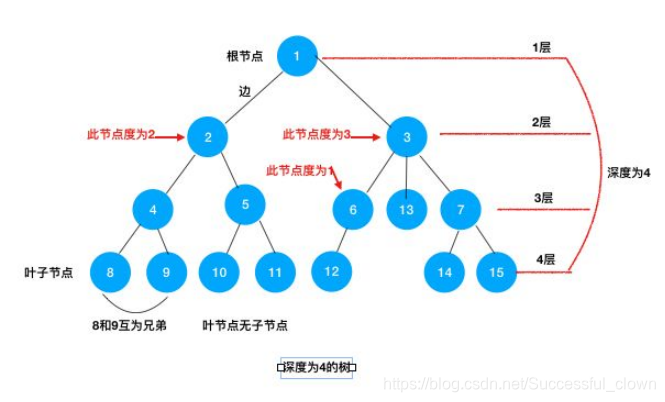
3. 节点的度:一个节点含有的子树的个数称为该节点的度;
树的度:一棵树中,最大的节点的度称为树的度;

在这里插入图片描述

二.二叉树的性质

1. 二叉树中,第 i 层最多有 2^i-1 个结点。
如果二叉树的深度为k,那么此二叉树最多有2^k-1个结点
二叉树中,终端结点数(叶子结点数)为n0,度为2的结点数为n2,则n0 = n2 + 1.
2. 如果二叉树中除了叶子结点,每一个结点的度都为2,则此二叉树称为满二叉树.
3. 如果二叉树中除去最后一层节点为满二叉树,且最后一层的结点依次从左到右分布,则此二叉树被称为完全二叉树.
**4.**顺序存储:将数据结构存储在固定的数组中,然在遍历速度上有一定的优势,但因所占空间比较大,是非主流二叉树。二叉树通常以链式存储。

class Tree(object):
    """树类"""
    def __init__(self, root=None):
        self.root = root
    def add(self, elem):
        """为树添加节点"""
        node = Node(elem)
        #如果树是空的,则对根节点赋值
        if self.root == None:
            self.root = node
        else:
            queue = []
            queue.append(self.root)
            #对已有的节点进行层次遍历
            while queue:
                #弹出队列的第一个元素
                cur = queue.pop(0)
                if cur.lchild == None:
                    cur.lchild = node
                    return
                elif cur.rchild == None:
                    cur.rchild = node
                    return
                else:
                    #如果左右子树都不为空,加入队列继续判断
                    queue.append(cur.lchild)
                    queue.append(cur.rchild)

三.二叉树的遍历

1. 遍历是指对树中所有结点的信息的访问,即依次对树中每个结点访问一次且仅访问一次,我们把这种对所有节点的访问称为遍历.

def breath travel(self,root):
    if root == None:
        return
    queue = []
    queue.append(root)
    while queue:def breadth_travel(self, root):
    """利用队列实现树的层次遍历"""
        node = queue.pop(0)
        print(node.elem,end=",")
        if node.lchild != None:
            queue.append(node.lchild)
        if node.rchild != None:
            queue.append(node.rchild)
    print()

先序遍历：每遇到一个节点，先访问，然后再遍历其左右子树
中序遍历：第一次经过时不访问根节点，等遍历完左子树之后再访问，然后遍历右子树
后序遍历：第一次和第二次经过时都不访问，等遍历完该节点的左右子树之后，最后访问该节点

class Node(object):
    """
    二叉树节点对象封装的类
    """

    def __init__(self, element):
        self.element = element
        self.lchild = None
        self.rchild = None

    def __str__(self):
        return self.element


    def __repr__(self):
        return  self.element


class Tree(object):
    """二叉树的封装"""

    def __init__(self, root=None):
        self.root = root

    def add(self, item):
        """往二叉树里面添加元素"""
        node = Node(item)
        #  #如果树是空的,则对根节点赋值
        if not self.root:
            self.root = node
        else:
            # 先找树的根节点, 存储到变量queue中
            queue = []
            queue.append(self.root)
            while queue:
                item = queue.pop(0)
                if not item.lchild:
                    item.lchild = node
                    return
                elif not item.rchild:
                    item.rchild = node
                    return
                else:
                    queue.append(item.lchild)
                    queue.append(item.rchild)

    def breadth_travel(self):
        """利用队列实现树的层次遍历"""
        if not self.root:
            return
        else:
            queue = []
            queue.append(self.root)
            while queue:
                node = queue.pop(0)
                print(node.element, end=',')
                if node.lchild:
                    queue.append(node.lchild)
                if node.rchild:
                    queue.append(node.rchild)
            print()


    def preorder(self, root):
        """先序遍历: 根左右"""
        if root == None:
            return
        print(root.element, end=', ')
        self.preorder(root.lchild)
        self.preorder(root.rchild)

    def inorder(self, root):
        """递归实现中序遍历"""
        if root == None:
            return
        self.inorder(root.lchild)
        print(root.element, end=', ')
        self.inorder(root.rchild)

    def lastorder(self, root):
        """递归实现后序遍历"""
        if root == None:
            return
        self.lastorder(root.lchild)
        self.lastorder(root.rchild)
        print(root.element, end=', ')


    def depth(self, root):
        """求二叉树的深度"""
        if root == None:
            return  0
        lcount = self.depth(root.lchild) + 1  # 树左侧的深度
        rcount = self.depth(root.rchild) + 1
        return  lcount if lcount > rcount else rcount


    def mirror(self, root):
        """对于二叉树进行一个镜像：左右子树交换"""
        if root == None:
            return  None
        self.mirror(root.lchild)
        self.mirror(root.rchild)
        root.lchild, root.rchild = root.rchild, root.lchild

if __name__ == '__main__':
    tree = Tree()
    for item in range(10):
        tree.add(item + 1)
    print("创建树成功")

    #
    # print("层次遍历".center(30, '*'))
    # tree.breadth_travel()


    print("先序遍历")
    root = tree.root
    tree.preorder(root)


    print("\n后序遍历")
    root = tree.root
    tree.lastorder(root)



    print("进行树的镜像".center(50, '*'))
    tree.mirror(root)
    print("层次遍历".center(30, '*'))
    tree.breadth_travel()

四.二叉排序树

**1.**二叉排序树要么是空二叉树，要么具有如下特点：

二叉排序树中，如果其根结点有左子树，那么左子树上所有结点的值都小于根结点的值；
二叉排序树中，如果其根结点有右子树，那么右子树上所有结点的值都大小根结点的值；
二叉排序树的左右子树也要求都是二叉排序树；

2 二叉树的操作

查找：对比节点的值和关键字，相等则表明找到了；小了则往节点的左子树去找，大了则往右子树去找，这么递归下去，最后返回布尔值或找到的节点。
插入：从根节点开始逐个与关键字进行对比，小了去左边，大了去右边，碰到子树为空的情况就将新的节点链接。
删除：如果要删除的节点是叶子，直接删；如果只有左子树或只有右子树，则删除节点后，将子树链接到父节点即可；如果同时有左右子树，则可以将二叉排序树进行中序遍历，取将要被删除的节点的前驱或者后继节点替代这个被删除的节点的位置。

如果要删除的节点是叶子，直接删；
如果只有左子树或只有右子树，则删除节点后，将子树链接到父节点即可；
如果同时有左右子树，(两种方式)则可以将二叉排序树进行中序遍历，取将要被删除的节
点的前驱或者后继节点替代这个被删除的节点的位置。
方法一:令结点 p 的左子树为其双亲结点的左子树；结点 p 的右子树为其自身直接前驱结点的右子树
方法二:用结点 p 的直接前驱（或直接后继）来代替结点 p，同时在二叉排序树中对其直接前驱（或直接后继）做删除操作。在对左图进行中序遍历时，得到的结点 p 的直接前驱结点为结点 s，所以直接用结点 s 覆盖结点 p
代码示例：

class Node(object):
    """二叉树节点对象的封装"""

    def __init__(self, element):
        self.element = element
        self.lchild = None
        self.rchild = None

    def __str__(self):
        return '<Node:%d>' % (self.element)


class BinarySortTree(object):
    """二叉排序树的封装"""

    def __init__(self):
        self.root = None

    def is_empty(self):
        return self.root is None

    def add(self, item):
        """
        树里面插入元素
            1. 先判断树是否为空， 直接让根结点指向新的节点
            2. 如果不为空:
                从根结点开始访问， 判断一下item和节点的大小;
                    如果大于节点元素， 往右孩子节点添加；
                    如果小于节点元素， 往左孩子节点添加；
        """
        node = Node(item)
        if self.root is None:
            self.root = node
        bt = self.root
        while True:
            rootItem = bt.element
            # 如果添加的元素是否大于根结点元素：
            if item > rootItem:
                # 如果根结点的右子树为空， 直接添加节点到右子树即可；
                if bt.rchild is None:
                    bt.rchild = node
                # 如果根结点的右子树不为空， 将右子树节点作为新的根结点， 循环继续判断;；
                bt = bt.rchild
            elif item < rootItem:
                if bt.lchild is None:
                    bt.lchild = node
                bt = bt.lchild
            # 如果插入的元素和根结点相等， 不做操作;
            else:
                return

    def breadth_travel(self):
        """利用队列实现树的层次遍历"""
        if not self.root:
            return
        else:
            queue = []
            queue.append(self.root)
            while queue:
                node = queue.pop(0)
                print(node.element, end=',')
                if node.lchild:
                    queue.append(node.lchild)
                if node.rchild:
                    queue.append(node.rchild)
            print()

    def search(self, root, key):
        """
        搜索指定元素是否在树里面
            key: 用户搜索的元素
        """
        if root is None:
            return False
        # 如果找到节点元素和用户搜索的值相等， 直接返回节点对象
        if root.element == key:
            return root
        # 如果找到节点元素大于用户搜索的值， 直接返回节点对象
        elif root.element > key:
            return self.search(root.lchild, key)
        else:
            return self.search(root.rchild, key)

    def searchDetail(self, root, parent, key):
        """
        搜索指定元素是否在树里面, 如果有， 则
        返回3个值:
            1. Bool: 是否找到该元素;
            2. node: 找到元素对应的节点
            3. parent: 找到的元素对应的父节点;
        """
        if root is None:
            return False, root, parent
        # 如果找到节点元素和用户搜索的值相等， 直接返回节点对象
        if root.element == key:
            return True, root, parent
        # 如果找到节点元素大于用户搜索的值， 直接返回节点对象
        elif root.element > key:
            return self.searchDetail(root.lchild, root, key)
        else:
            return self.searchDetail(root.rchild, root, key)

    def delete(self, key):
        """
        删除二叉排序树的节点元素:
            1). 如果要删除的节点是叶子，直接删；
            2). 如果只有左子树或只有右子树，则删除节点后，将子树链接到父节点即可；
        :param key:
        :return:
        """
        # 1. 查找删除元素对应的节点, isExists是否找到该节点元素， node是找到的节点对象， parent：元素节点的父节点
        isExists, node, parent = self.searchDetail(self.root, None, key)

        if not isExists:
            print("要删除的元素%d不存在" % (key))
            return

        # 如果深处的是根节点， 不处理
        if node == self.root:
            print("不能删除根结点")
            return
        # 1). 如果要删除的节点是叶子，直接删；
        if node.lchild is None and node.rchild is None:
            # 判断删除的节点是父节点左孩子还是右孩子
            if parent.lchild == node:
                parent.lchild = None
            else:
                parent.rchild = None

        # 2). 如果只有左子树或只有右子树，则删除节点后，将子树链接到父节点即可；
        # 如果只有左子树
        if node.lchild is not None and node.rchild is None:
            # 如果node是parent的左子树：
            if parent.lchild == node:
                parent.lchild = node.lchild
            else:
                parent.rchild = node.lchild

        # 如果只有右子树
        if node.rchild is not None and node.lchild is None:
            # 如果node是parent的左子树：
            if parent.lchild == node:
                parent.lchild = node.rchild
            else:
                parent.rchild = node.rchild

        # 如果有左右子树
        # 方法一: 令结点 node 的左子树为其双亲结点的左子树；结点 node的右子树为其自身直接前驱结点的右子树
        if node.lchild is not None and node.rchild is not None:
            # 如何找到node的直接前驱节点, 找到后， 将直接前驱节点的右子树指向node的右子树;
            # 当前节点左子树的最右节点
            # 分类讨论， 删除的是父节点的左孩子还是右孩子
            if parent.lchild == node:
                parent.lchild = node.lchild
            else:
                parent.rchild = node.lchild

            prevNode = node.lchild
            while prevNode.rchild:
                prevNode = prevNode.rchild
            # prev指的是node节点的直接前驱(中徐遍历时，node节点前面的节点)
            prevNode.rchild = node.rchild

if __name__ == '__main__':
    # sortedTree = BinarySortTree()
    # nums = [3, 5, 7, 2, 1]
    # for num in nums:
    #     sortedTree.add(num)
    #
    # sortedTree.breadth_travel()
    #
    # print("搜索:")
    # print(sortedTree.search(sortedTree.root, 2))
    #
    # print("详细搜索:")
    # isExist, node, parentNode = sortedTree.searchDetail(sortedTree.root, None, 2)
    # print("找到的节点:", node)
    # print("搜索节点的父节点:", parentNode)
    #
    # print("删除节点")
    # sortedTree.delete(3)
    # sortedTree.breadth_travel()

    sortedTree = BinarySortTree()
    nums = [45, 12, 53, 3, 37, 100, 24, 52, 61, 90, 78]
    for num in nums:
        sortedTree.add(num)
    sortedTree.breadth_travel()
    # 删除右左右子树的节点;
    sortedTree.delete(53)
    sortedTree.breadth_travel()

五.平衡二叉树

1 平衡二叉树，又称为 AVL 树。遵循以下两个特点的二叉树：

每棵子树中的左子树和右子树的深度差不能超过 1；
二叉树中每棵子树都要求是平衡二叉树；
总结: 其实就是在二叉树的基础上，若树中每棵子树都满足其左子树和右子树的深度差都不超过 1，则这棵二叉树就是平衡二叉树。

2 平衡因子：每个结点都有其各自的平衡因子，表示的就是其左子树深度同右子树深度的差。
平衡二叉树中各结点平衡因子的取值可能是0，1，-1。

例题

1、输入一个二叉树，判断该二叉树是否为平衡二叉树。

    def IsBalanced_Solution(self, root):
        #问题转化为求二叉树的高度，并确定左右子树高度的绝对值之差<=1是否成立
        if root==None : 
        	return True
        lcount=self.TreeDepth(root.lchild)
        rcount=self.TreeDepth(root.rchild)
        return abs(lcount-rcount)<=1

2、输入一个二叉树，求该树的深度。从根结点到叶子结点依次经过的结点(含根、叶结点形成的一条路径，最长的路径的长度为树的深度)

def TreeDepth(self, root):
    if root==None:return 0
    lcount=self.TreeDepth(root.lchild)+1
    rcount=self.TreeDepth(root.rchild)+1
    return lcount if lcount>rcount else rcount