素数筛法

素数定义

质数又称素数。一个大于1的自然数，除了1和它自身外，不能被其他自然数整除的数叫做质数；否则称为合数（规定1既不是质数也不是合数）。

素数判断

 

设n为要判断的数。按照定义，判断n是否能被2~n-1中任意一个数整除即可。时间复杂度为O(n)

bool prime(int n)
{
    if(n==1)                    //如果n为1，则n不是素数返回false
        return false;
    for(int i = 2; i < n; i++)
    {
        if(n%i==0)              //如果n被除1以及n以外的自然数整除那么n不是素数，返回false
            return false;
    }
    return true;                //返回true
}

这里有一种升级版本

只需要判断n是否能被2~√n中任意一个数整除即可。这是为什么呢？

举个例子，一个合数n能被i整除，商为j，那么一定存在i*j=n，一定存在i<=√n<=j，所以如果一个数在2~√n范围内没有被整除，那么这个数一定是素数

该升级版本时间复杂度为O(√n)

bool prime(int n)
{
    if(n==1)                    //如果n为1，则n不是素数返回false
        return false;
    for(int i = 2; i*i <= n; i++)
    {
        if(n%i==0)              //如果n被除1以及n以外的自然数整除那么n不是素数，返回false
            return false;
    }
    return true;                //返回true
}

 

素数筛法

当我们需要求一个区间[a,b]范围内的所有素数时，如果这个区间范围很大，就需要用到素数筛法了。

素数筛法就是根据已经求出来的素数，来将素数的倍数筛去，因为素数的倍数一定不是素数

埃氏筛法

思想：从2开始，将每个质数的倍数都标记成合数，以达到筛选素数的目的

代码：

int vis[maxn];                              //用来标记素数，素数标记为0，非素数为1
bool prime()
{
    memset(vis,0,sizeof(vis));              //初始都是素数
    vis[0]=vis[1]=1;                        //0和1都不是素数
    for(int i = 2; i <= maxn; i++)          //2一定是素数，所以从2开始可以不断筛出合数
    {
        if(!vis[i])                         //如果i是素数，让i的所有倍数都不是素数
        {
            for(int j = i*i; j<=maxn; j+=i)  //
            {
                vis[j] = 1;
            }
            cout<<endl;
        }
    }
}

 这里有一个优化，j并不是从i+i开始的，这是因为i*（2-i-1）在2~i-1时已经筛去。

存在的问题：

同一个合数可能被不同的素数重复筛出。

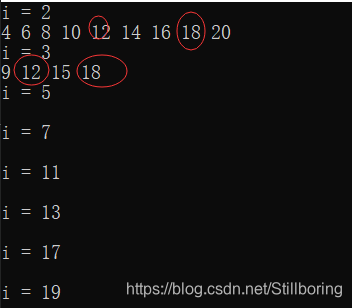
以图中的12为例，12是素数2和素数3的倍数，2*6=12  3*4=12，所以12就被筛了两次。

那么如何保证每个合数只被筛选一次呢？只需要保证每个合数被它的最小质因子筛选。这也就是欧拉筛法的思想

 

欧拉筛法

思路：在埃氏筛法的基础上，让每个合数只被它的最小质因子筛选一次，以达到不重复的目的。

代码：

#include <bits/stdc++.h>
using namespace std;
const int maxn = 20;
int vis[maxn];                              //用来标记素数，素数标记为0，非素数为1
int prime[maxn];                            //保存素数
bool Prime()
{
    int cnt = 0;                            //记录prime中素数的数量
    memset(vis,0,sizeof(vis));              //初始都是素数
    vis[0]=vis[1]=1;                        //0和1都不是素数
    for(int i = 2; i <= maxn; i++)          //2一定是素数，所以从2开始可以不断筛出合数
    {
        if(!vis[i])                         //如果i是素数，让i的所有倍数都不是素数
        {
            prime[cnt++]=i;
        }
        //以最小质因子的方式去筛选，而不是以素数的倍数的方式
        for(int j = 0; j<cnt&&i*prime[j]<=maxn; j++)
        {
            vis[i*prime[j]] = 1;
            if(i%prime[j]==0)
                break;
        }
        cout<<endl;
    }
}
int main()
{
    Prime();
    return 0;
}

①vis[i*prime[j]]不是用素数的倍数筛选，而是用prime数组中从小到大的素数作为最小质因子筛选。

②对于 i%prime[j] == 0 就break的解释 ：当 i是prime[j]的倍数时，i = kprime[j]，如果继续运算 j+1，i * prime[j+1] = prime[j] * k prime[j+1]，这里prime[j]是最小的素因子，当i = k * prime[j+1]时会重复，所以才跳出循环。

时间复杂度分析：求解[1，n]区间中的素数，每个合数只会被筛选一次，就是说每个数只会被标记一次，因此时间复杂度为O(n)

 

参考博文：https://blog.youkuaiyun.com/qq_39763472/article/details/82428602