傅里叶变换学习记录

原创

已于 2025-04-18 07:27:18 修改 · 827 阅读

29 ·

CC 4.0 BY-SA版权

文章标签：

#学习

于 2025-04-18 03:55:19 首次发布

系列文章目录

提示：写完文章后，目录可以自动生成，如何生成可参考右边的帮助文档

（1）差分（Differentiation）

前言

提示：这里可以添加本文要记录的大概内容：

傅里叶变换是信号处理中的一个非常重要的数学工具，它的核心思想是将复杂的信号分解成不同频率的正弦波的叠加。虽然看起来可能有点抽象，但可以通过一些通俗的例子和应用来帮助理解它在电子信息中的实际作用。

提示：首先粗略了解一下傅里叶变换......

一、傅里叶变换扫盲

1.1 基本概念

傅里叶变换的基本原理可以理解为：任何信号，都可以分解成不同频率的简单波形（正弦波和余弦波）的叠加。例如，一个复杂的音频信号，或者一个电压信号，虽然看起来非常复杂，但实际上它是由多种不同频率的简单正弦波构成的。

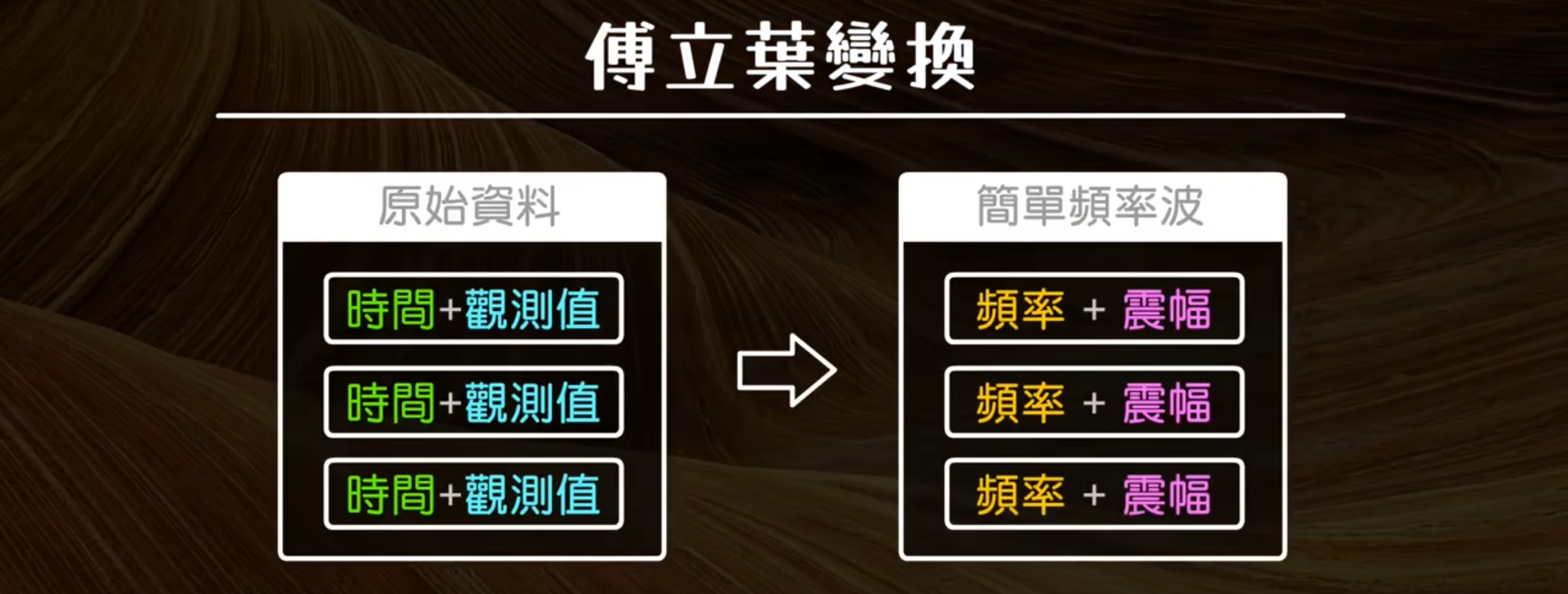
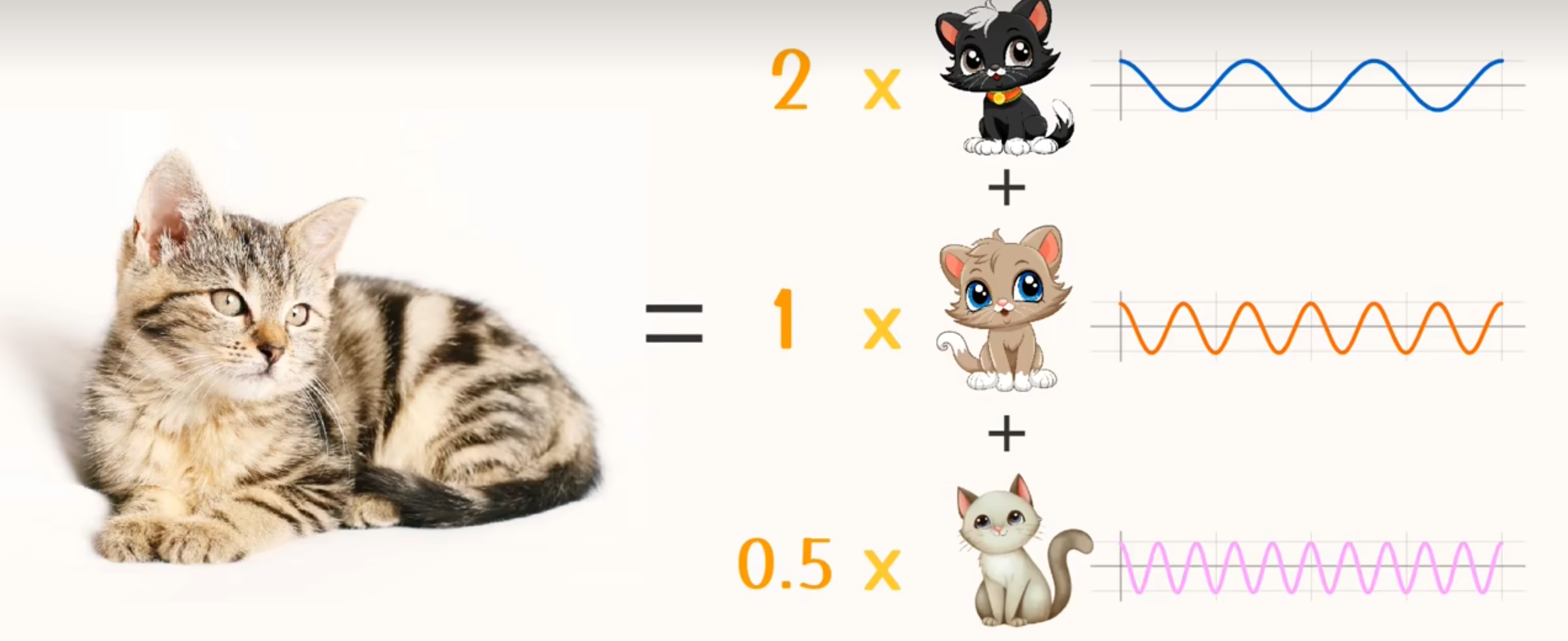
在数学上，傅里叶变换将一个信号（通常是时间域信号，如电压随时间变化的波形）转换到频率域（显示不同频率成分的幅度和相位信息），让我们可以更清楚地看到信号的频率特性。

1.2 通俗的例子

假设你在听音乐，音乐信号是由各种不同音高（频率）组成的。如果你想知道音乐中的每个音符的频率，傅里叶变换就可以帮你从复杂的音乐信号中提取出不同的频率成分。简单来说，就是：

听到一个声音，傅里叶变换可以告诉你，这个声音是由哪些频率的波组成的。

另一个简单的例子：

你观察一段电压波形，它可能是一个很复杂的波动，但傅里叶变换可以告诉你，这段波形实际上是由几个不同频率的正弦波组成的。

1.3 傅里叶变换在电子专业中的应用

作为电子信息类···专业的研究生，你会遇到许多与信号和频率相关的任务。以下是一些傅里叶变换在你专业中的具体应用：

信号分析与处理：在仪器仪表的测量系统中，常常需要处理复杂的信号。傅里叶变换可以帮助你将信号从时间域转换到频率域，从而更好地分析和理解信号的特性。例如，频谱分析：你可以通过傅里叶变换分析一个复杂的电压信号，看看它是由哪些频率成分组成的。通过分析频谱，你可以发现信号中的噪声频率、干扰信号或者有用的频率成分。
滤波与信号去噪：在仪器仪表中，信号往往会受到各种噪声的干扰。通过傅里叶变换，你可以识别噪声的频率成分，并通过滤波器将这些频率成分滤除。比如：如果你知道信号中有一个固定频率的噪声，你可以使用傅里叶变换来提取这个噪声频率，然后通过滤波器将它从信号中去除。
调制与解调：在通信系统中，信号通常会被调制到一个载波频率上，以便有效传输。傅里叶变换可以帮助你分析和解调这些信号。例如：在 调频（FM）或调幅（AM）通信系统 中，通过傅里叶变换，你可以从接收到的信号中提取出原始的低频信号（即你要传输的信息）。
振动分析与故障诊断：在电子仪器和机械系统中，振动分析是常用的故障诊断工具。通过傅里叶变换，你可以把机械振动信号从时间域转到频率域，从而分析出不同频率的振动成分。例如，在电动机的振动信号中，某些特定频率的振动可能表明电动机的某个部件有故障，傅里叶变换可以帮助你找到这些特征频率。
图像处理与边缘检测：在某些电子仪器中，图像处理是一个重要应用。傅里叶变换可以用来处理图像信号，尤其是在图像的频域分析中。例如：通过傅里叶变换，你可以对图像进行 边缘检测，即分析图像的频率成分，从而突出图像中的边缘信息。