C++ Binary_Search _Tree（1）

1.循环实现Erase

我们Erase 首先要找到我们要删的东西在不在 如果我们要删除一个不存在的东西

那肯定是直接返回false

找的规则符合搜索二叉树的性质

即

根的左节点的值及其子节点的值小于根节点的值

根的右节点的值及其子节点的值大于根节点的值

​bool Find(const K& key)
{
	Node* cur = _root;
while (cur)
{
	//第一步找到要删除的值 看存不存在
	if (cur->_key < key)
	{
		parent = cur;
		cur = cur->_right;
	}
	else if (cur->_key > key)
	{
		parent = cur;
		cur = cur->_left;
	}

    {
//存在



    }
}

//不存在
		return false;
	}

​

我们再来思考找到了要删的点

有哪几种情况

1. 左子树的值为空

2.右子树的值为空

3.左右子树的值都不为空

(1)左子树为空（左节点为空）

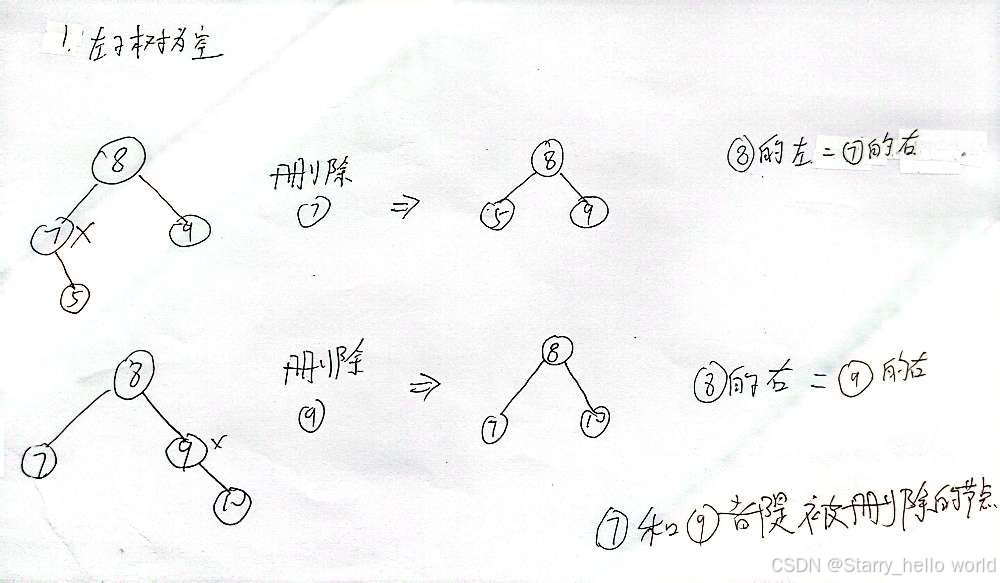
左子树删除的时候 我们要注意两点

1.是删除点的是父节点的左节点还是右节点

2.删除点父节点链接的是删除点的右节点（左节点为空）

就算右子树也是空也可以链接

但是我们再思考一些特殊情况  比如删除的是根呢？

如果删除的是根 它不就没有父节点吗？

那上面两点是不是就不成立 这种情况我们就要去单独写了！

那很简单

 

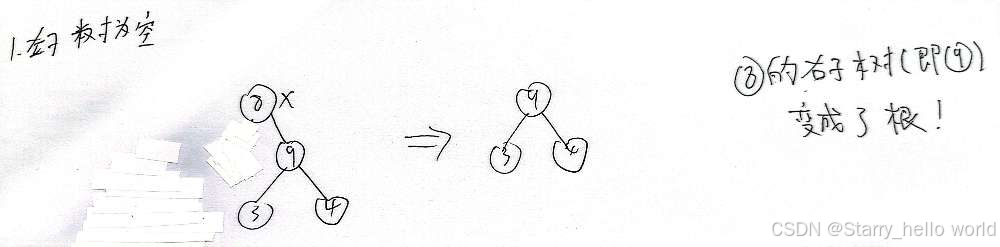
所以对于删除的是根就很简单

1.根的右节点为新的根 

 这样左为空就可以很好的写出来 右为空的情况同理

	else // 找到了 要判断要删的值是那张情况   1.左为空  2.右为空  3.左右都不为空
	{
		// 左为空 
		if (cur->_left == nullptr)
		{
			if (cur == _root)
			{
				_root = cur->_right;
			}
			else
			{
				//判断要删除的节点是父节点的左节点还是右节点
				if (parent->_right == cur)
				{
					parent->_right = cur->_right;
				}
				else
				{
					parent->_left = cur->_right;
				}
			}
		}// 右为空
		else if (cur->_right == nullptr)
		{
			if (cur == _root)
			{
				_root = cur->_left;
			}
			else
			{
				if (parent->_right == cur)
				{
					parent->_right = cur->_left;
				}
				else
				{
					parent->_left = cur->_left;
				}
			}
		}

我们再来思考最后一种情况

左右子树都为空

这种情况就比较难了

我能不能直接把这个节点删了

但是删了之后父节点连接哪个子节点呢？（左右都不为空）

这样就很麻烦 要不断的调整

搜索二叉树的性质是

根的左节点的值及其子节点的值小于根节点的值
根的右节点的值及其子节点的值大于根节点的值

因此在中序遍历的时候 二叉树是满足从小到大的顺序

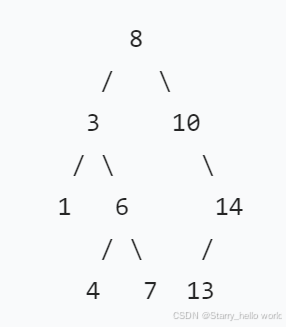
中序遍历是 1  3  4 6 7 8 10 13  14

我们先看整个树

   很明显

根左边的数（左节点及左节点下面的所有节点）都小于根的值

根左边的数（右节点及右节点下面的所有节点）都大于根的值

也就是如果我把8删掉了

这个树就变成了

1  3  4 6 7  10   13  14

这个顺序我们可以写出两种情况

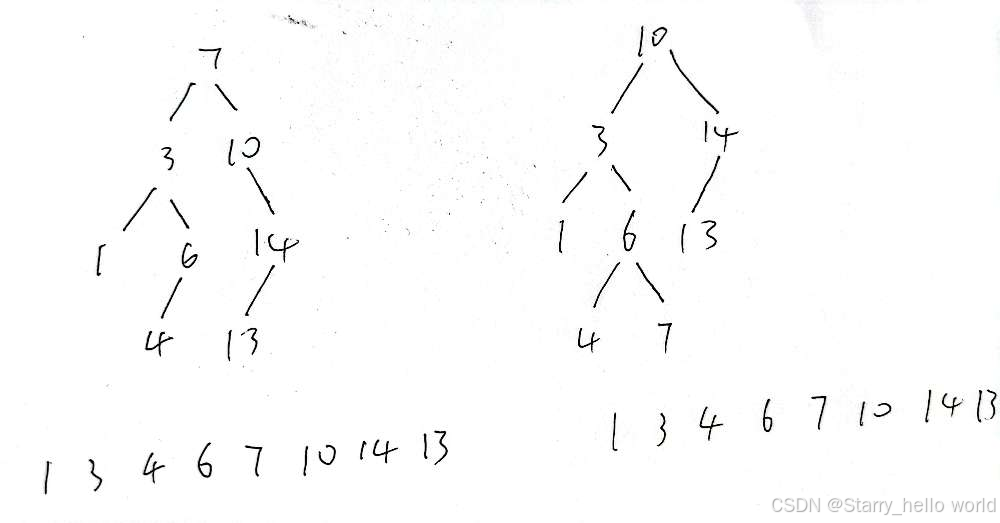
我们发现其他元素的相对位置不变

 只把根节点左边的7变成根或者把右边的10变成根

但是很巧的是

7是根左边最大的  10是根右边最大的

原理是这样的

由于搜索二叉树的性质

性质1：根节点的值>左边所有值

性质2：根节点的值<右边所有值

新的根节点的值也要满足这点

如果要在左边节点找这样一个值是不是要找左边最大的

因为只有左边最大的变成了根后（不再是左边的值）  就大于所有左边的值 这样就满足性质1了

同时也满足性质2了

为什么？

左边最大的<原来的根节点

原来根节点<右边的所有值

就可以得到

左边最大的<右边的所有值

所以就左边的最大的值变成根后依然满足性质2

右边最小的值可以作为根 同理

那根据搜索二叉树的性质找到左边最小的值是不是很简单

首先找到根的左节点

再一直往右走 直到遇到空停止  空的父节点就是根左边最大的最大值

右边最小值同理（这里只演示一种）

那这样不就完成了左右都不为空的情况了吗？

那如果我删的左右都不为空的节点不是根怎么办？

那你就把它看成根去处理不久可以了吗？

比如像右图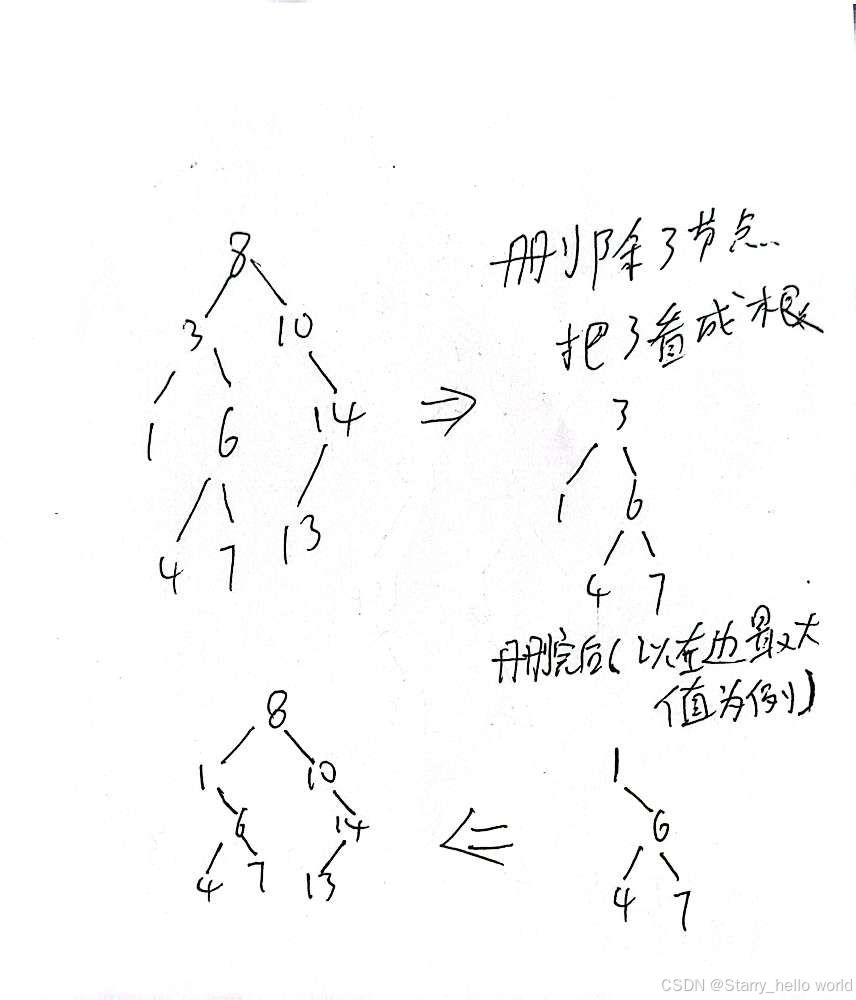

我们找到新的根节点后 链接的时候也要分情况讨论

 

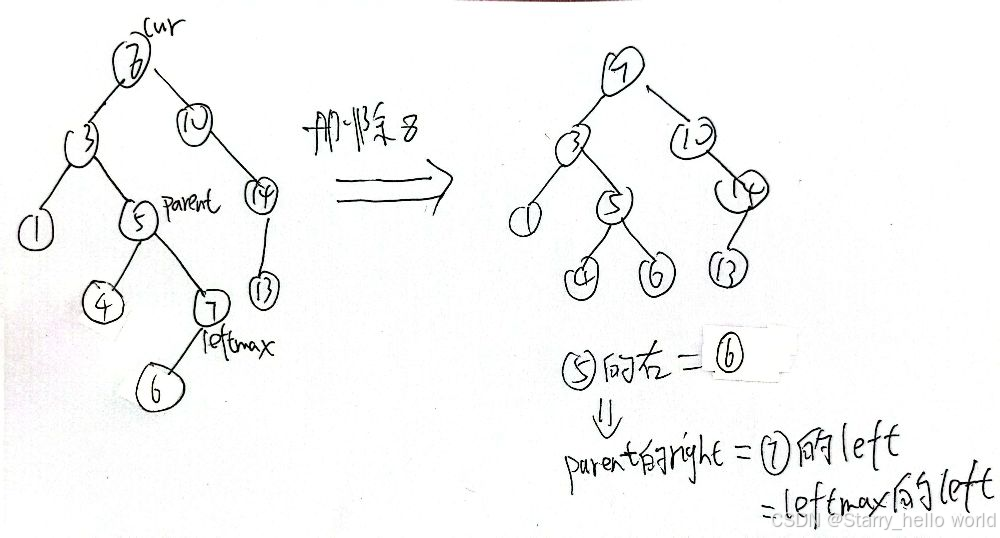
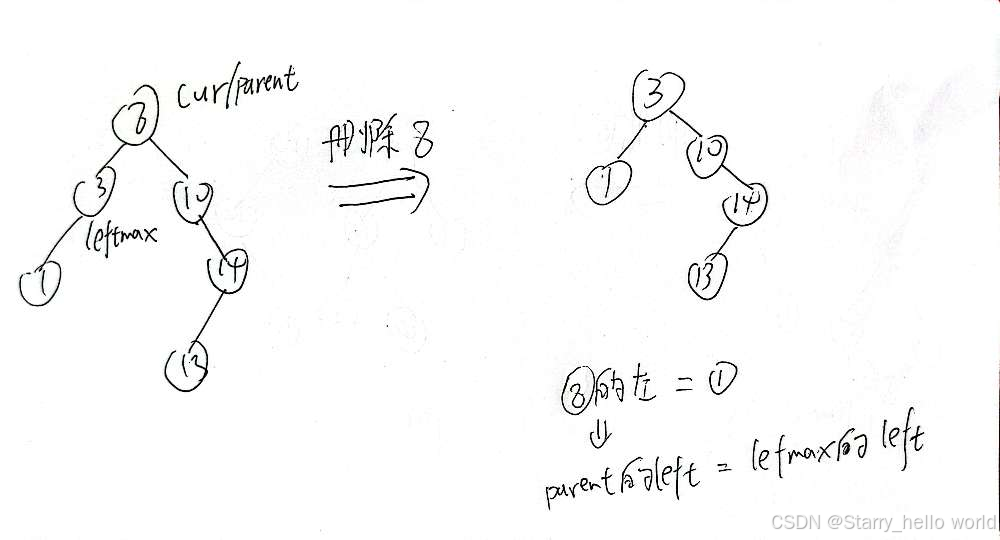
	else
	{
		// 找替代节点
		Node* parent = cur;//这个地方parent可不可以为nullptr 
		//不可以 如果删除的是根节点就会报错啊！根节点没有parent啊！
		Node* leftMax = cur->_left;
		while (leftMax->_right)
		{
			parent = leftMax;
			leftMax = leftMax->_right;
		}
		//这个地方交换的是节点的指向值，交换的不是cur和leftmax指向的节点
		swap(cur->_key, leftMax->_key);
		//这个地方判断的是左边是其父节点的左节点还是右节点 判断的是节点 而不是节点指向的值
		if (parent->_left == leftMax)
		{
			parent->_left = leftMax->_left;
		}
		else
		{
			parent->_right = leftMax->_left;
		}

		cur = leftMax;
	}

	delete cur;
	return true;
}

 三种情况都写完了 完整的循环版的Erase是不是就出来了！

bool Erase(const K& key)
{
	Node* parent = nullptr;
	Node* cur = _root;

	while (cur)
	{
		//第一步找到要删除的值 看存不存在
		if (cur->_key < key)
		{
			parent = cur;
			cur = cur->_right;
		}
		else if (cur->_key > key)
		{
			parent = cur;
			cur = cur->_left;
		}
		else // 找到了 要判断要删的值是那张情况   1.左为空  2.右为空  3.左右都不为空
		{
			// 左为空 
			if (cur->_left == nullptr)
			{
				if (cur == _root)
				{
					_root = cur->_right;
				}
				else
				{
					//判断要删除的节点是父节点的左节点还是右节点
					if (parent->_right == cur)
					{
						parent->_right = cur->_right;
					}
					else
					{
						parent->_left = cur->_right;
					}
				}
			}// 右为空
			else if (cur->_right == nullptr)
			{
				if (cur == _root)
				{
					_root = cur->_left;
				}
				else
				{
					if (parent->_right == cur)
					{
						parent->_right = cur->_left;
					}
					else
					{
						parent->_left = cur->_left;
					}
				}
			} // 左右都不为空 
			else
			{
				// 找替代节点
				Node* parent = cur;//这个地方parent可不可以为nullptr 
				//不可以 如果删除的是根节点就会报错啊！根节点没有parent啊！
				Node* leftMax = cur->_left;
				while (leftMax->_right)
				{
					parent = leftMax;
					leftMax = leftMax->_right;
				}
				//这个地方交换的是节点的指向值，交换的不是cur和leftmax指向的节点
				swap(cur->_key, leftMax->_key);
				//这个地方判断的是左边是其父节点的左节点还是右节点 判断的是节点 而不是节点指向的值
				if (parent->_left == leftMax)
				{
					parent->_left = leftMax->_left;
				}
				else
				{
					parent->_right = leftMax->_left;
				}

				cur = leftMax;
			}

			delete cur;
			return true;
		}
	}

	return false;
}

 2.递归实现Erase

3.搜索二叉树的优缺点

二叉树搜索的时间复杂度是O（n）而不是O（log2 N）

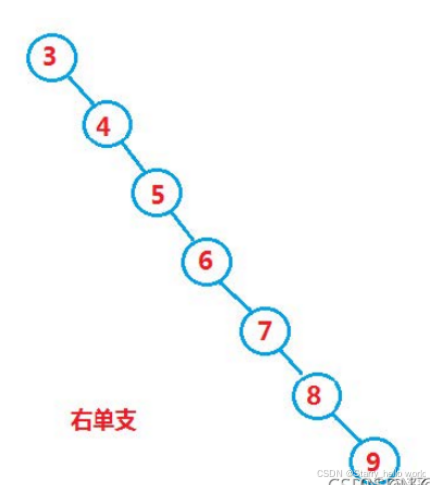
对于左边这种时间复杂度是O（N）

右边这种时间复杂度就是O（log2 N）

但是我们一般取最大的也就是O（N）

 我们再来看二分查找 二分查找查找的效率很高 没有问题

但是删除或者插入挪动数据的效率很差

二分查找不能用链表的结构 因为链表不能用下标随时访问

用数组的结构 插入删除效率又不行

物理空间连续  下表随机访问 要同时满足

于是搜索二叉树出现了

排序 中序就可以排序

插入 查找 最多只有高度次

删除虽然复杂些 但是效率也不低 基本也是高度次

缺点 ：下限没有保障 就如上面所说 差的时候 时间复杂度可以是O(n)

2.递归实现Erase

	//递归实现Erase
	bool _EraseR(Node*& root, const K& key)
	{
		if (root == nullptr)
			return false;

		if (root->_key < key)
		{
			return _EraseR(root->_right, key);
		}
		else if (root->_key > key)
		{
			return _EraseR(root->_left, key);
		}
		else
		{
			Node* del = root;

			// 1、左为空
			// 2、右为空
			// 3、左右都不为空
			if (root->_left == nullptr)
			{
				root = root->_right;
			}
			else if (root->_right == nullptr)
			{
				root = root->_left;
			}
			else
			{
				Node* leftMax = root->_left;
				while (leftMax->_right)
				{
					leftMax = leftMax->_right;
				}

				swap(root->_key, leftMax->_key);

				return _EraseR(root->_left, key);
				//这个地方写  return _EraseR(leftmax, key);不可以
				//因为leftmax是函数内的局部针变量 出了函数无法使用（使用就是野指针）
			}
			delete del;
			return true;
		}
	}

首先 递归的Erase和循环的Erase一样都要去寻找我们删除的那个值是否已经存在

找到了同样分三种情况

1.左为空 2.右为空  3.左右都不为空

（1）左为空或者右为空

这个地方我们对于左为空 右为空和循环的处理方式不一样

我们不用去保存父节点 以及判断删除的点是  父节点的左节点还是右节点

这个地方用的是引用 比如我在过程递归过程中

return _EraseR(root->_right, key);

如果走这个说明下一个递归函数的root节点是其父节点的右节点

    return _EraseR(root->_left, key);

如果走这个说明下一个递归函数的root节点是其父节点的左节点

同时这个递归函数的参数是引用啊 你参数改变的同时 你父节点指向的左节点/右节点也会跟着变啊！

为什么循环不能用？ 因为引用无法改变指向啊！ 但是递归 每递归一次 就是创建一个新的引用 

当然可以用啦！

（2）左右都不为空

这个时候同理我们要找到左边最大值或者右边最小值（以左边最大值为例子）

那我们可不可以用递归

答案是不能 这样会破坏搜索二叉树的结构

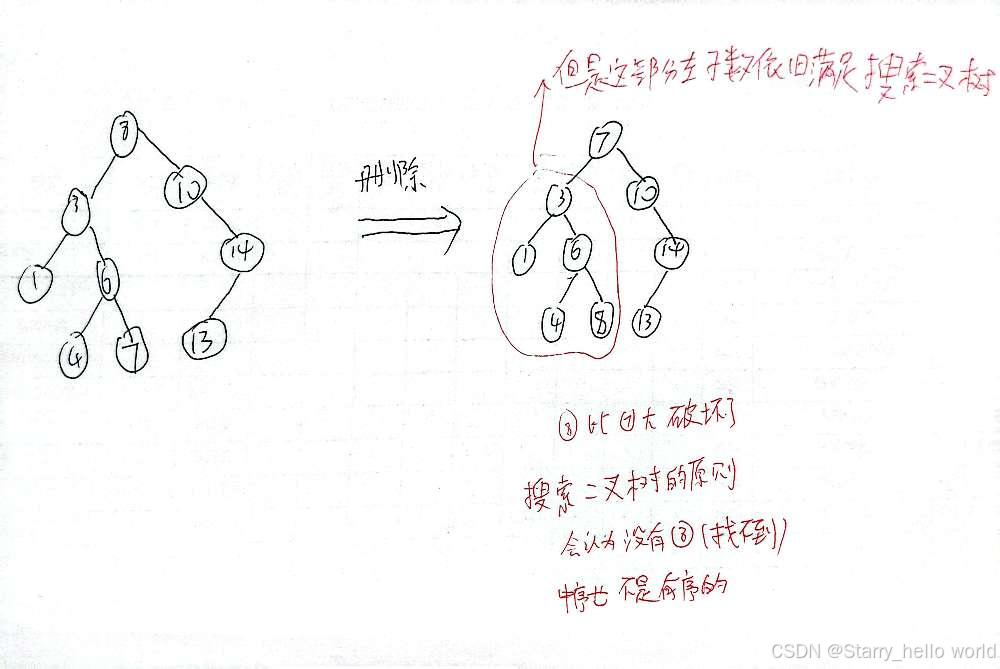
你会发现我们破坏了搜索二叉树后你就找不到那个要删的8了

这个时候你要删8 你递归进去 8比7大 走右边  然后你就永远找不到8了（8在左边）

但是转换一下 我们去左子树递归不就可以了吗（以左子树最大值为例）

为什么左子树可以？

下图除了7和8 其它的值都是是满足搜索二叉树

那么原本7那个地方应该是左子树最大的值

但是根（8）比左边最大的值还大 还过去也满足是左子树最大的值

除去根的部分或者除去8的部分都可构成搜索树 但是我们要找的就是8 所以不能把除8的部分看成搜索树

（3）leftmax和root->left的区别

 我们再来思考一下 return _EraseR(root->_left, key);

可以改成return _EraseR(leftmax, key);吗？

答案是不可以 

因为正常我们如果要根据左子树找到删除的节点

（1）至少再递归一次

我们如果找的不是Node* leftMax = root->_left

基本上要至少再递归一次递归寻找

我们后面要链接父节点和删除节点的子节点
也就需要保存父节点并判断删除节点是父节点的左节点还是右节点

但是递归寻找return _EraseR(root->_right, key);

或  return _EraseR(root->_left, key);

就已经把删除节点是父节点左节点还是右节点判断好了

（2）一次都不递归

如果一次都不递归 我传leftmax过去

我就无法判断删除节点是父节点的左节点还是右节点

那就更无法链接了

因为直接传leftmax传的是绝对位置

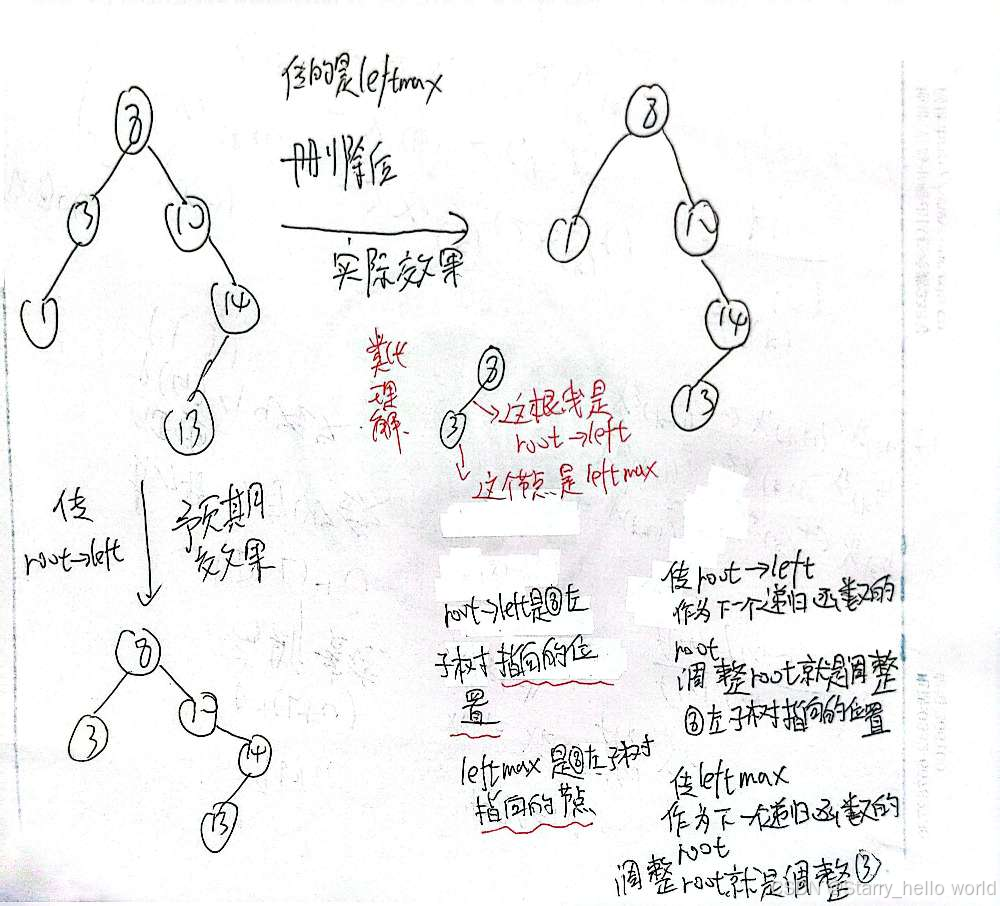
 传root->left可以理解为传一个相对位置的指针  即指向root的左子树节点  传的是一个抽象的节点指针

传leftmax可以理解为传一个绝对位置的节点  是一个指向具体的节点的指针（即原先root左子树准确的节点）