POJ1328,Radar Installation,贪心，仰慕逆向思维

Radar Installation

Description

Assume the coasting is an infinite straight line. Land is in one side of coasting, sea in the other. Each small island is a point locating in the sea side. And any radar installation, locating on the coasting, can only cover d distance, so an island in the sea can be covered by a radius installation, if the distance between them is at most d. 

We use Cartesian coordinate system, defining the coasting is the x-axis. The sea side is above x-axis, and the land side below. Given the position of each island in the sea, and given the distance of the coverage of the radar installation, your task is to write a program to find the minimal number of radar installations to cover all the islands. Note that the position of an island is represented by its x-y coordinates. 
 
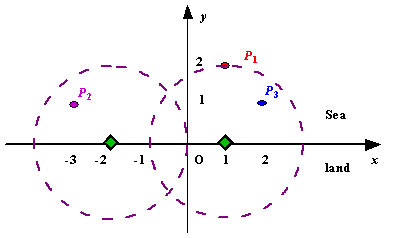
Figure A Sample Input of Radar Installations

Input

The input consists of several test cases. The first line of each case contains two integers n (1<=n<=1000) and d, where n is the number of islands in the sea and d is the distance of coverage of the radar installation. This is followed by n lines each containing two integers representing the coordinate of the position of each island. Then a blank line follows to separate the cases. 

The input is terminated by a line containing pair of zeros 

Output

For each test case output one line consisting of the test case number followed by the minimal number of radar installations needed. "-1" installation means no solution for that case.

Sample Input

3 2
1 2
-3 1
2 1

1 2
0 2

0 0

Sample Output

Case 1: 2

Case 2: 1

分析：

对这题 的第一印象是从输入之后对每个点一横坐标为第一要素纵坐标为第二要素排序。然后从最左边一个点的横坐标开始枚举，在包含第一个点的情况下尽量右移包含更多的点，知道第一个点不再包含则停止。雷达数加一，开始下一次移动。早上翘了五节课，还被逮到了T_T。。。按着思路敲出的代码给出的两组数据能过，提交发现无限WA。。。后来看了disscuss发现一种用逆向思维的方法，以每个小岛为圆心画圆，记录在X轴上截下的区间。对所有区间按起点排序。之后就是考虑去掉重叠区间的问题了。

code:

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
#define MAX 1000
using namespace std;
typedef struct length
{
    double lf,rg;
}len;
len l[MAX+5];
bool cmp(len a,len b)
{
    if(a.lf==b.lf) return a.rg<b.rg;
    return a.lf<b.lf;
}
int main()
{
    int n,count=0,i;
    double tmp,x,y,sq,d;
    while(scanf("%d %lf",&n,&d)==2)
    {
        if(n==0&&d==0) break;
        int inst=1;
        bool flag=true;
        count++;
        for(i=0;i<n;i++)
        {
            scanf("%lf %lf",&x,&y);
            sq=sqrt(d*d-y*y);
            if(y<0||y>d) flag=false;
            l[i].lf=x-sq;
            l[i].rg=x+sq;
        }
        if(!flag||d<=0)
        {
            printf("Case %d: %d\n",count,-1);
            continue;
        }
        sort(l,l+n,cmp);
        tmp=l[0].rg;
        for(i=1;i<n;i++)
        {
            if(l[i].lf>tmp)
            {
                inst++;
                tmp=l[i].rg;
            }
            else if(l[i].rg<tmp)
                tmp=l[i].rg;
        }
        printf("Case %d: %d\n",count,inst);
    }
    return 0;
}