开源仓库
https://github.com/zzySerendipity/MaxPlusII_Experiments/tree/main如果仓库的代码对你有帮助记得Star！
MaxPlusII设计 3x3阵列乘法器
全加器
已知：
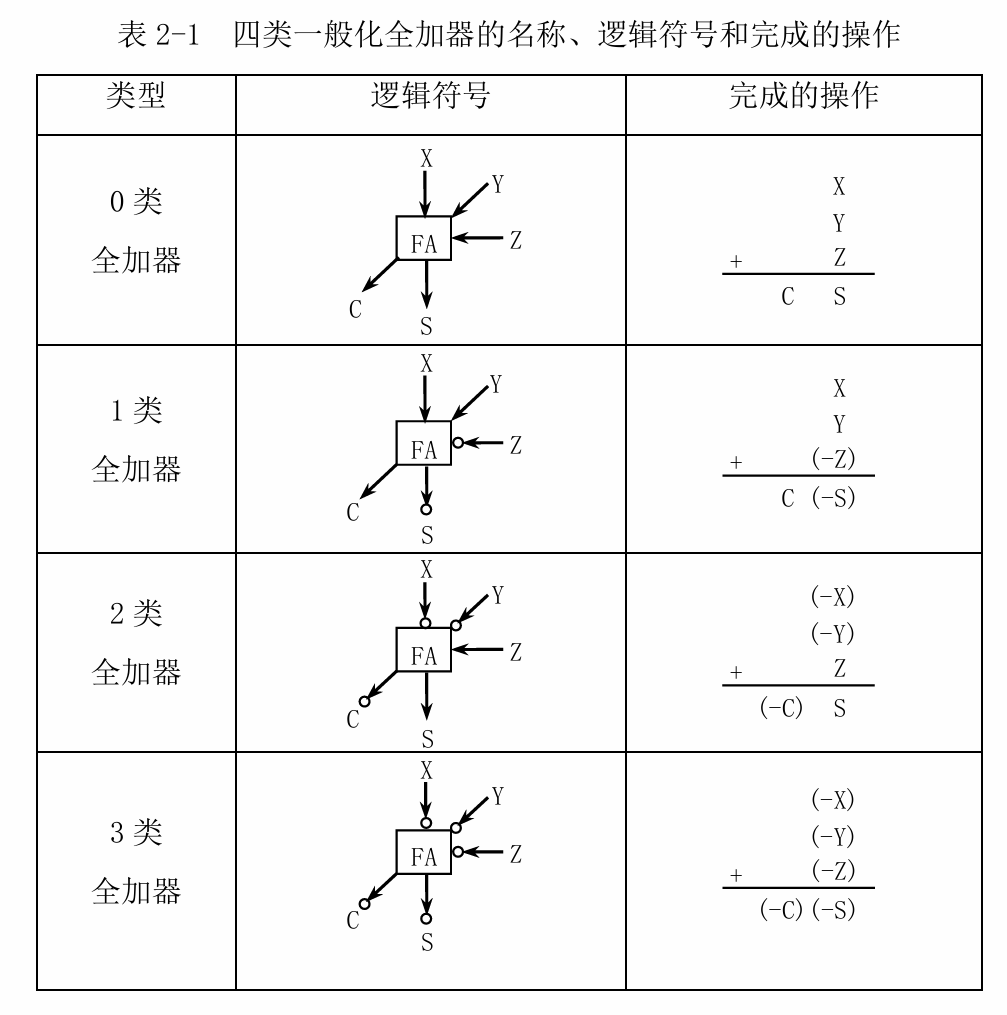
根据表2-1，可以推导出这四类全加器S和C的逻辑表达式。
Si = Xi ⊕ Yi ⊕ Zi-1
Ci = XiYi + Zi-1(Xi + Yi)
-
对0类、3类全加器而言有：
-
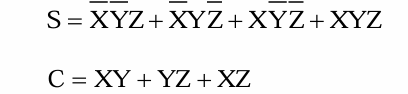
对1类、2类全加器，则有：
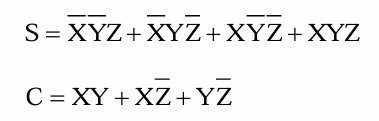
0类和3类全加器中S和C的逻辑表达式相同，它和常规的全加器是一致的。1类和2类全加器中S 和C的逻辑表达式也是相同的。
阵列乘法器逻辑原理
注意理解输入的符号位 和 输出的 补充符号位。
全加器图元设计
对0类、3类全加器而言，完成FA0图元设计：
采取VHDL语言设计图元形式：
LIBRARY IEEE;
USE IEEE.STD_LOGIC_1164.ALL;
USE IEEE.STD_LOGIC_ARITH.ALL;
USE IEEE.STD_LOGIC_UNSIGNED.ALL;
-- ENTITY FA0
ENTITY FA0 IS
PORT(
X,Y,Z:IN STD_LOGIC;
S,C:OUT STD_LOGIC
);
END FA0;
ARCHITECTURE A OF FA0 IS
BEGIN
S<=(NOT X AND NOT Y AND Z)OR(NOT X AND Y AND NOT Z)OR(X AND NOT Y AND NOT Z)OR(X AND Y AND Z);
C<=(X AND Y)OR(Y AND Z)OR(X AND Z);
END A; 对1类、2类全加器而言，完成FA1图元设计：
LIBRARY IEEE;
USE IEEE.STD_LOGIC_1164.ALL;
USE IEEE.STD_LOGIC_ARITH.ALL;
USE IEEE.STD_LOGIC_UNSIGNED.ALL;
ENTITY FA1 IS
PORT(
X,Y,Z:IN STD_LOGIC;
S,C:OUT STD_LOGIC
);
END FA1;
ARCHITECTURE A OF FA1 IS
BEGIN
S<=(NOT X AND NOT Y AND Z)OR(NOT X AND Y AND NOT Z)OR(X AND NOT Y AND NOT Z)OR(X AND Y AND Z);
C<=(X AND Y)OR(X AND NOT Z)OR(Y AND NOT Z);
END A; 3x3 阵列乘法器图元设计
top顶层需要使用总线的形式输入与输出，因此在顶层文件中，我们所涉及的3x3 阵列乘法器 需要作为一个“元件”加入到top层中。
Multiple-array：
输入总线与阵列图元设计
ANDARRAY：
LIBRARY IEEE;
USE IEEE.STD_LOGIC_1164.ALL;
USE IEEE.STD_LOGIC_ARITH.ALL;
USE IEEE.STD_LOGIC_UNSIGNED.ALL;
ENTITY ANDARRAY IS
PORT(
A, B : IN STD_LOGIC_VECTOR(2 DOWNTO 0);
A0B0, A1B0, A0B1, A0B2, A2B0, A1B1, A1B2, A2B1, A2B2 : OUT STD_LOGIC
);
END ANDARRAY;
ARCHITECTURE A OF ANDARRAY IS
BEGIN
A0B0 <= A(0) AND B(0);
A1B0 <= A(1) AND B(0);
A0B1 <= A(0) AND B(1);
A0B2 <= A(0) AND B(2);
A2B0 <= A(2) AND B(0);
A1B1 <= A(1) AND B(1);
A1B2 <= A(1) AND B(2);
A2B1 <= A(2) AND B(1);
A2B2 <= A(2) AND B(2);
END A;输出总线图元设计
CONVERT：
LIBRARY IEEE;
USE IEEE.STD_LOGIC_1164.ALL;
USE IEEE.STD_LOGIC_ARITH.ALL;
USE IEEE.STD_LOGIC_UNSIGNED.ALL;
ENTITY CONVERT IS
PORT(
I0, I1, I2, I3, I4, I5 : IN STD_LOGIC;
P : OUT STD_LOGIC_VECTOR(5 DOWNTO 0)
);
END CONVERT;
ARCHITECTURE A OF CONVERT IS
BEGIN
-- P <= (I5, I4, I3, I2, I1, I0);
P(0) <= I0;
P(1) <= I1;
P(2) <= I2;
P(3) <= I3;
P(4) <= I4;
P(5) <= I5;
END A;顶层gdf文件设计
WaveForm仿真运行
与顶层top.gdf同名！！：top.scf
运行结果：
结果分析：
由于输入端为3位，因此在直接补码阵列乘法器中，只能完成 - 4 ~ + 3 之间的乘法运算。
MaxPlusII设计 4x4阵列乘法器
设计4x4 输入的阵列乘法器，可以完成 - 8 ~ + 7 之间的乘法运算。结果输出总线也会相应增加。
全加器设计
多位乘法在直接阵列乘法器中，采用的加法器相同。
共需12个全加器，其中3个O类，3个一类，6个二类全加器。
全加器设计与3x3阵列乘法器完全相同。
4x4 阵列乘法器图元设计
通过理解指导书中的3x3 阵列乘法器设计思路完成：
设计原理图
红色括号是带符号位，由上两行确定中间的四行。根据符号位可以确定输入端的权值。
逻辑原理图
由各个全加器的输入端的正负权值分类确定C 与 S两个输出位的正负权。从而确定该全加器是0、1、2类全加器（本例用不到3类全加器）。
图元内部结构图
Graphic Edit
由上分析可知，FA1包含1类和2类全加器。一类全加器在Z输入端口为负权，而二类全加器在Z输入端口为正权。
注意：FA0 FA1的三输入端 X Y Z 不能随意指定引脚，需要考虑该类全加器在 Z 端口输入值得正负权，依照上图逻辑原理图绘制
1类与2类全加器FA1，在XYZ三个输入端有区别：一类全加器在Z输入端口为负权，而二类全加器在Z输入端口为正权。
因此设计电路图时，要根据逻辑原理图确保输入端口正确接线
4x4 阵列乘法器图元设计实例图：
此图不可以画错！每个全加器的三个输入端XYZ并不都是完全一样的，也就是说对于全加器的输入选择，不是任意的！
原因见上，写在这里不过是为了在提醒以下，因为笔者在测试时发生了错误，经过来回推敲确定是这里的问题。
输入总线与阵列图元设计
剩下的就是老规矩了，和3x3阵列乘法器相似：编写VHDL语言，保存后生成图元文件。但要注意PORT部分会存在细微差别。
ANDARRAY:
LIBRARY IEEE;
USE IEEE.STD_LOGIC_1164.ALL;
USE IEEE.STD_LOGIC_ARITH.ALL;
USE IEEE.STD_LOGIC_UNSIGNED.ALL;
ENTITY ANDARRAY IS
PORT(
A, B : IN STD_LOGIC_VECTOR(3 DOWNTO 0);
A0B0, A1B0, A0B1, A0B2, A2B0, A1B1, A1B2, A3B0, A2B1, A0B3, A1B3, A3B1, A2B2, A3B2, A2B3, A3B3 : OUT STD_LOGIC
);
END ANDARRAY;
ARCHITECTURE A OF ANDARRAY IS
BEGIN
A0B0 <= A(0) AND B(0);
A1B0 <= A(1) AND B(0);
A0B1 <= A(0) AND B(1);
A0B2 <= A(0) AND B(2);
A2B0 <= A(2) AND B(0);
A1B1 <= A(1) AND B(1);
A1B2 <= A(1) AND B(2);
A2B1 <= A(2) AND B(1);
A2B2 <= A(2) AND B(2);
A3B0 <= A(3) AND B(0);
A0B3 <= A(0) AND B(3);
A1B3 <= A(1) AND B(3);
A3B1 <= A(3) AND B(1);
A3B2 <= A(3) AND B(2);
A2B3 <= A(2) AND B(3);
A3B3 <= A(3) AND B(3);
END A;输出总线图元设计
CONVERT:
LIBRARY IEEE;
USE IEEE.STD_LOGIC_1164.ALL;
USE IEEE.STD_LOGIC_ARITH.ALL;
USE IEEE.STD_LOGIC_UNSIGNED.ALL;
ENTITY CONVERT IS
PORT(
I0, I1, I2, I3, I4, I5, I6, I7 : IN STD_LOGIC;
P : OUT STD_LOGIC_VECTOR(7 DOWNTO 0)
);
END CONVERT;
ARCHITECTURE A OF CONVERT IS
BEGIN
-- P <= (I7, I6, I5, I4, I3, I2, I1, I0);
P(0) <= I0;
P(1) <= I1;
P(2) <= I2;
P(3) <= I3;
P(4) <= I4;
P(5) <= I5;
P(6) <= I6;
P(7) <= I7;
END A;顶层gdf文件设计
保证对齐！这里我的ANDARRAY与阵列图元的输出引脚顺序错了，图没有更新。如果使用上述代码生成图元需要注意和Multiple-Array图元输入端相应引脚相连。
正常且美观的情况下，不会出现下面的那两个“结”。
WaveForm仿真运行
运行结果：
结果分析：
输入范围： - 8 ~ + 7
输入样例：
Final
嘿嘿，总觉得要有头有尾。
开源Github仓库（首尾交相呼应）：zzySerendipity/MaxPlusII_Experiments: 计算机组成（原理）与体系结构课程实验：使用ＭaxPlusII软件进行设计，完成3x3位直接补码阵列乘法器，并拓展完成4x4位直接补码阵列乘法器（源码与设计教程）。
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
